原标题:生活中的数学之奇妙的蜂窝构造
采得百花成蜜后,为谁辛苦为谁甜。
————《峰》罗隐
辛勤劳作的蜜蜂是大自然的精灵,而他们用集体的智慧构筑的蜂窝更是大自然鬼斧神工的代表作。
蜂窝构造非常精巧、实用而且节省材料。蜂房是由无数个大小相同的房孔组成,每个房孔都是正六角形,且都被其它房孔包围,两个房孔之间只隔着一堵蜡制的墙。蜜蜂的身体基本上是圆柱形,蜂在房孔内既不会有多余的空间又不感到拥挤。房孔的底既不是平的,也不是圆的,而是尖的,这个底是由三个完全相同的菱形组成。有人测量过菱形的角度,两个钝角都是109°而两个锐角都是70°。令人叫绝的是,世界上所有蜜蜂的蜂窝都是按照这个统一的角度和模式建造的。

古希腊哲学家帕珀斯认为蜜蜂们被赋予了「某种几何方面的先见之明」。但智慧来源呢,难道是上帝吗?William Kirby在1852年称,「蜜蜂是神明教导过的数学家」。Grafissimo / Getty也曾说到:蜜蜂似乎已经进化出使用分泌的软蜡去构筑完美六角形巢室的能力。然而,一些研究人员认为,软蜡表面的均匀张力促使其收缩为面积最小的形状,就像泡筏上面裂变出的气泡。
生物学家认为世界上的所有蜂巢具有这样的精巧特点,都按照这个标准去建造,主要是因为自然对象的形成和生长受到周围空间和材料的影响。因此,蜜蜂为了能更好适应自然环境,节省建造材料等等,就选择六边形为基本结构来建造蜂巢。
那么,六边形有什么特点使得自然界对它一再青睐呢?自然对象的形成和生长受到周围空间和材料的影响。正六边形是能够不重叠地铺满一个平面的三种正多边形(正六边形、正方形和正三角形)之一。在这三种正多边形中,六边形以最小量的材料占有最大面积。
正六边形的另一特点是它有六条对称轴。因此它可以经过各式各样的旋转而不改变形状。能用最小表面积包围最大容积的球也与六边形相联系。当一些球互相挨着被放入一个箱子中时,每一个被包围的球与另外六个球相切。当我们在这些球之间画出一些经过切点的线段时,外切于球的图形正好是一个正六边形。

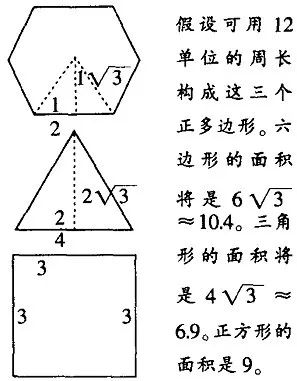
一般在没有特殊说明的情况下,我们说的六边形指的都是凸六边形。
根据多边形内角和公式S=180°·(n-2),所有的六边形的内角和都是720°,外角和为360°。
六边形当中最特殊的图形就是正六边形,我们把六条边都相等,六个内角都相等的多边形称之为正六边形。根据六边形的外角和等于360度,那么它的各内角相等,推出一个内角为180-(360/6)=120度,所以正六边形每一个内角为120度。

同时由于正六边形的特殊性,正六边形可以分成过中心6个全等的正三角形,作正三角形的高,就可以得到一些特殊的量,如下图所示:
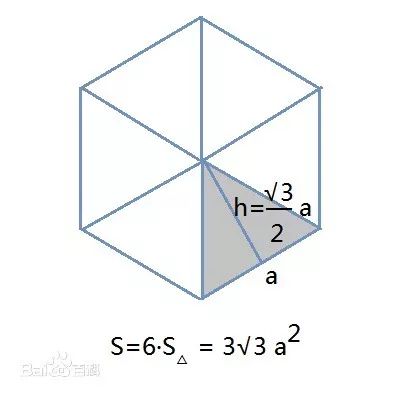
蜂房的结构引起了科学家们的极大兴趣。经过对蜂房的深入研究,科学家们开发出了具有蜂窝结构的材料,在工程应用中的各种场合大显身手:在陆地上,我们可以看到装备有蜂窝结构轮胎的越野车;在天空中,装备有蜂窝结构的除噪材料,让我们的旅途更加舒适;蜂窝结构在建筑业中的应用也非常广泛。

从数学的角度看,用不重叠摆放的多边形把平面的一部分完全覆盖用形状和大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺;通常把这类问题叫做用多边形的平面镶嵌。
现实生活中,我们已经看到了用正多边形或不规则的基本图形拼成各种各样的图案,让我们的生活变得丰富多彩,这就是利用数学来美化我们生活最经典的例子之一。
作者:暮知秋,中国科学院数学与系统科学研究院
图片来源:百度
来源:中国科学院数学与系统科学研究院返回搜狐,查看更多
责任编辑:
最后
以上就是激动耳机最近收集整理的关于C语言六边形蜂巢数组,生活中的数学之奇妙的蜂窝构造的全部内容,更多相关C语言六边形蜂巢数组,生活中内容请搜索靠谱客的其他文章。








发表评论 取消回复