第十三届蓝桥杯【蜂巢】最简单的解法

第十三届蓝桥杯【蜂巢】最简单的解法

• 题目：
  
• 思路

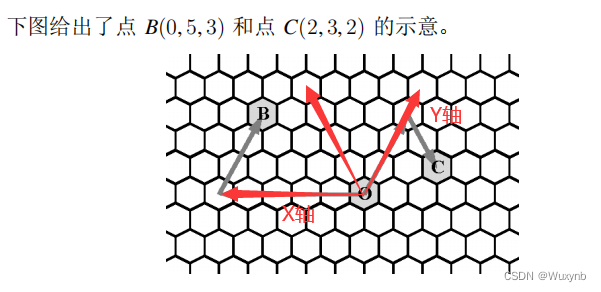
1. 总共有六个方向如下，可以按如下图方式作为x轴（这里的方向标反了，标的方向是x轴的负方向）和y轴：
   
2. 此时六个方向 $0-5$ 可以用如下数组操作：
   $int[][]dirs=newint[][]-1,0,-1,1,0,1,1,0,1,-1,0,-1;$
   往$0$方向，走x坐标减一；往 $1$ 方向走，x坐标减一，y坐标加一；往$2$方向走，y坐标加一；往 $3$ 方向走，x坐标加1；往 $4$ 方向走，则x坐标加一，y坐标减一；往$5$方向走则y坐标减一。
3. 然后，我们现在只关心让第一个点 $(x1,y1)$ 作为左边的点（例如图中 $B$ 点），让第二点 $(x2,y2)$ 为在右边的点（例如图中 $C$ 点），然后我们只要考虑两种情况：

1. 当第一个点在第二点左上方时，途中 $B$ 和 $C$ 点的位置关系，此时 $B$ 点在坐标中的位置是 $(-5,3)$，而$C$点位置为 $(2,1)$ ，从左上往右下走，x坐标在加，y坐标在减，故此时最短距离为$B$从左上向右下走2步到达 $(-3,1)$ ，再向右走5步就能到达$C$点，此时有 $a=Math.abs(-5-2)=7，b=Math.abs(3-1)=2$，故此时距离为 $dis=Math.max(a,b)=7$ ，即能得到此时两点的距离公式为 $dist=Math.max(Math.abs(x1-x2),Math.abs(y1-y2))$。
2. 当第一个点在第二个点左下方时，图中 $O$ 点和 $C$ 点的位置关系，此时 $O$ 点坐标为 $(0,0)$ ，$C$ 点坐标为 $(2,1)$，此时 $O$ 点到 $C$ 点最短距离为 $O$ 先向右走两步，再向上（Y）走一步到达 $C$ ，此时有 $a=Math.abs(0-2)=2,b=Math.abs(0-1)=1$，故此时距离为 $dis=a+b=3$，即此时距离公式为 $dist=Math.abs(x1-x2)+Math.abs(y1-y2)$。
3. 当第一个点在第二点的左方时放过来即可（比如 $B$ 在 $C$ 的右上方等价于 $C$ 在 $B$ 的左下方，$B$ 在 $C$ 的右下方等价于 $C$在 $B$ 的左上方）。

• AC代码如下：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 65536);
    static StringTokenizer tokenizer = new StringTokenizer("");

    public static void main(String[] args) {
        int[][] dirs = new int[][]{{-1, 0}, {-1, 1}, {0, 1}, {1, 0}, {1, -1}, {0, -1}};
        int d1 = nextInt(); long p1 = nextLong(), q1 = nextLong();
        int d2 = nextInt(); long p2 = nextLong(), q2 = nextLong();
        long x1 = 0, y1 = 0, x2 = 0, y2 = 0;
        x1 += p1 * dirs[d1][0] + q1 * dirs[(d1 + 2) % 6][0];
        y1 += p1 * dirs[d1][1] + q1 * dirs[(d1 + 2) % 6][1];
        x2 += p2 * dirs[d2][0] + q2 * dirs[(d2 + 2) % 6][0];
        y2 += p2 * dirs[d2][1] + q2 * dirs[(d2 + 2) % 6][1];
        System.out.println(getDistance(x1, y1, x2, y2));
    }

    public static long getDistance(long x1, long y1, long x2, long y2) {
        if (x1 > x2) return getDistance(x2, y2, x1, y1); // 如果 (x1, y1)在右边，则翻转一下。
        long a = Math.abs(x1 - x2), b = Math.abs(y1 - y2); 
        if (y1 >= y2) return Math.max(a, b); // 当第一个点在左上方时
        return a + b; // 当第一个点在左下方时
    }

    private static String next() {
        while (!tokenizer.hasMoreTokens()) {
            try {
                tokenizer = new StringTokenizer(br.readLine());
            } catch (IOException e) {
                e.printStackTrace();
            }
        }
        return tokenizer.nextToken();
    }

    public static int nextInt() { return Integer.parseInt(next()); }

    public static long nextLong() { return Long.parseLong(next()); }
}

最后

以上就是甜蜜纸鹤为你收集整理的第十三届蓝桥杯【蜂巢】最简单的解法的全部内容，希望文章能够帮你解决第十三届蓝桥杯【蜂巢】最简单的解法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。