神经网络实现Mnist手写数字识别笔记1.Mnist手写数字识别介绍2.神经网络架构介绍3.代码实现4.运行结果5.代码中部分方法介绍

57 阅读 0 评论 38 点赞

我是靠谱客的博主糟糕草莓，最近开发中收集的这篇文章主要介绍神经网络实现Mnist手写数字识别笔记1.Mnist手写数字识别介绍2.神经网络架构介绍3.代码实现4.运行结果5.代码中部分方法介绍，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1.Mnist手写数字识别介绍

2.神经网络架构介绍

3.代码实现

4.运行结果

5.代码中部分方法介绍

1.Mnist手写数字识别介绍

Mnist手写数字识别是Kaggle上一个很经典的机器学习数据集，里边包括55000张训练数据和10000张图片的测试数据，每张图片大小为28*28像素的单通图片。该任务为通过机器学习来识别图片中的数字属于0，1，2，3，4，5，6，7，8，9中那个，是个典型的多分类问题，以至于Tensorflow在其example中加入了该数据集，并提供了相应的实现方法。

图片长什么样呢？展示如下：

2.神经网络架构介绍

神经网络在设计开始前，我们只能知道多少个训练样本、多少个特征和最终需要怎样的结果，对于中间层的神经元个数都是未知的，这常常需要在训练过程中进行大量调整。对于手写数字识别问题，我们知道训练样本为28*28的单通道灰度图像，训练样本有55000个，最终要得出每张图片的分类到底是数字0，1，2，3，4，5，6，7，8，9中哪一类。也就是说这是一个10分类问题。

神经网络每一层的神经元个数和层数虽说有很大的经验成分，但是神经元个数要和在输入数据维数和输出数据维数之间相“契合”。对于神经网络来说，输入的一张28*28像素的图像是将其“压扁”为784像素的一维向量，这784个像素点作为784个特征。一张图像有784个特征，那么将N张图像同时输入，则相当于将N*784的数据输入。这里的N通常是批量处理时每一次输入数据的批量大小，比如本例子中我们每次遍历输入100张图片，那么N就是100。

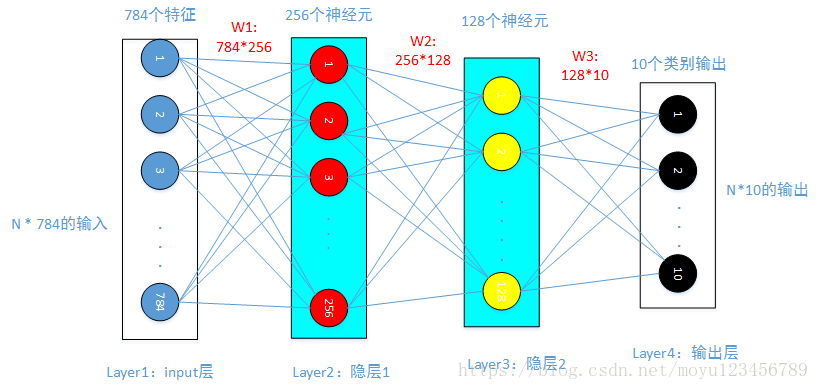
神经网络中，上一层的输出作为下一层的输入。计算主要包括线性计算和非线性计算，线性计算就是x*w+bias，非线性计算则是对x*w+bias的计算结果进行非线性激活，比如sigmod（）函数和ReLu（max(0, x*w+bias）函数。本例子对网络架构定义如下图所示，除了输入层和输出层外，增加了两个隐藏层。请注意在下图中两个有背景色的隐层一和隐层二中，通过线性计算后都有非线性计算。通过隐层一和隐层二（相当于两个黑盒子）来提取特征，然后和W3相乘进行线性计算，并将计算结果输入到softmax分类器中得到loss值。

隐藏层1设计了256个神经元，隐藏层2设计了128个神经元。那么，我们就可以推导出W1和W2的大小。W1维度为:784*256，W2维度为：256*128，W3维度为：128*10。如果以sigmod函数为非线性函数的话，该图的计算表达式为：f = w3*(sigmod(w2*(sigmod(w1*x+b))+b))+b。其中sigmod(w1*x+b)是隐层1的计算结果，sigmod(w2*(sigmod(w1*x+b))+b)为隐层2的计算结果。至此，特征提取完成。w3*(sigmod(w2*(sigmod(w1*x+b))+b))+b就是本神经网络输入到softmax分类器中的输入值。

3.代码实现

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
#获取手写字体识别数据
mnist = input_data.read_data_sets('data/', one_hot=True)

#网络架构定义
#第一个隐层有256个神经元
n_hidden_1 = 256 
#第二个隐层有128个神经元
n_hidden_2 = 128
#输入的样本有784个特征 
n_input    = 784
#手写字分为0 1 2....9这10个类别
n_classes  = 10  

# 输入和输出
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])
    
# 各层网络参数定义
stddev = 0.1
weights = {
    'w1': tf.Variable(tf.random_normal([n_input, n_hidden_1], stddev=stddev)),
    'w2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2], stddev=stddev)),
    'out': tf.Variable(tf.random_normal([n_hidden_2, n_classes], stddev=stddev))
}
biases = {
    'b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'out': tf.Variable(tf.random_normal([n_classes]))
}

#前向传播计算
def multilayer_perceptron(_X, _weights, _biases):
    #根据输入_X计算第一层
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(_X, _weights['w1']), _biases['b1']))
    #以第一层layer_1作为输入计算第二层
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, _weights['w2']), _biases['b2']))
    #以第二层layer_2作为输入计算第三层，也就是计算输出层
    return (tf.matmul(layer_2, _weights['out']) + _biases['out'])

# 前向传播进行预测
pred = multilayer_perceptron(x, weights, biases)

#求损失函数
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
#使用随机梯度下降进行优化
optm = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost)
#预测值和真实标签进行对比，tf.argmax(pred, 1)返回的是pred中最大值的索引号
#tf.equal将预测的值和标签值进行比较，相同为True,不相同为False
corr = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
#tf.cast为类型转换函数，将corr转换为float类型数据 
accr = tf.reduce_mean(tf.cast(corr, "float"))

# INITIALIZER
init = tf.global_variables_initializer()

#训练200个epoch
training_epochs = 200
#每一个batch取100个样本
batch_size      = 100
display_step    = 4
# LAUNCH THE GRAPH
sess = tf.Session()
sess.run(init)
# 遍历epoch
for epoch in range(training_epochs):
    avg_cost = 0.
    #计算batch次数
    total_batch = int(mnist.train.num_examples/batch_size)
    # 遍历batch
    for i in range(total_batch):
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        feeds = {x: batch_xs, y: batch_ys}
        sess.run(optm, feed_dict=feeds)
        avg_cost += sess.run(cost, feed_dict=feeds)
    avg_cost = avg_cost / total_batch
    # DISPLAY
    if (epoch+1) % display_step == 0:
        print ("Epoch: %03d/%03d cost: %.9f" % (epoch, training_epochs, avg_cost))
        feeds = {x: batch_xs, y: batch_ys}
        train_acc = sess.run(accr, feed_dict=feeds)
        print ("TRAIN ACCURACY: %.3f" % (train_acc))
        feeds = {x: mnist.test.images, y: mnist.test.labels}
        test_acc = sess.run(accr, feed_dict=feeds)
        print ("TEST ACCURACY: %.3f" % (test_acc))
print ("OPTIMIZATION FINISHED")

4.运行结果

运行结果如下，可以看出经过200轮训练后，得到的测试精确度达到了0.884。

Epoch: 003/200 cost: 2.278398191
TRAIN ACCURACY: 0.260
TEST ACCURACY: 0.198
Epoch: 007/200 cost: 2.245890754
.......
Epoch: 191/200 cost: 0.457598143
TRAIN ACCURACY: 0.920
TEST ACCURACY: 0.883
Epoch: 195/200 cost: 0.452329346
TRAIN ACCURACY: 0.860
TEST ACCURACY: 0.883
Epoch: 199/200 cost: 0.447292094
TRAIN ACCURACY: 0.910
TEST ACCURACY: 0.884
OPTIMIZATION FINISHED

5.代码中部分方法介绍

1.tf.random_normal

功能：tf.random_normal()函数用于从服从指定正太分布的数值中取出指定个数的值。
函数声明：tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
参数：shape: 输出张量的形状，必选
mean: 正态分布的均值，默认为0
stddev: 正态分布的标准差，默认为1.0
dtype: 输出的类型，默认为tf.float32
seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样
name: 操作的名称

2.tf.nn.softmax_cross_entropy_with_logits

https://blog.csdn.net/m0_37041325/article/details/77040060?utm_source=blogxgwz0 这篇博客对此有比较详细的介绍，这个也是神经网络的一个重点知识点。

3.tf.equal(x, y, name=None)

功能：tf.equal用于判断x和y是否相等，对于单个值直接进行判断，相同返回True，不同返回False。对于向量则遍历相同位置的数进行判断，返回值也是向量，相同时对应位置为True，不相同时对应位置为False。

4.tf.cast(x, dtype, name=None)

功能：tf.cast为类型转换函数，将x转换为dtype类型数据。

5.tf.argmax(vector, 1)

功能：tf.argmax(vector, 1)返回的时vector中最大值的索引。如果vector是一个向量，那就返回其中最大值的索引，如果是一个矩阵，那就返回一个向量，这个向量的每一维都是对应矩阵行的最大值元素索引号。

代码github链接：https://github.com/zhuwsh/mnist-master

注意：本文为唐宇迪老师神经网络课程笔记。当执行mnist = input_data.read_data_sets('data/', one_hot=True)因为各种原因（比如下载超时）而获取不到数据集时，可以在网上直接搜索下载mnist数据集。或者从github链接https://github.com/zhuwsh/mnist-master获取。