神经网络前向传播 w的维度与含义

  我们都知道神经网络中每一个隐层都有参数w和b，输入x首先要乘以w再加上b，最后传入激活函数就会得到这个隐层的输出。——但是，具体w是什么形状、它和x怎么乘、加上的b是在哪里之类的一直不是很清晰，因为在一些算法讲义里这一块一讲起来就容易用各种符号，看起来很复杂（虽然它并不难），而且这方面细节也并不耽误我们去定义和使用神经网络，所以就似懂非懂了。

  但后来在学习推荐系统、word2vector之类的时候，就经常得用到训练好的权重，所以清楚其维度与意义是非常重要的。

  以一个简单的神经网络来举例子（如图）：有三个层，三个神经元的输入层、两个神经元的隐层以及一个神经元的输出层。

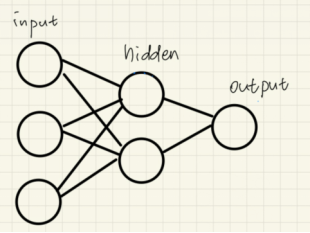
  关于w，b以及各种乱七八糟的到底是啥、在哪的问题——

  直接放图！（涂涂改改画了挺久）：

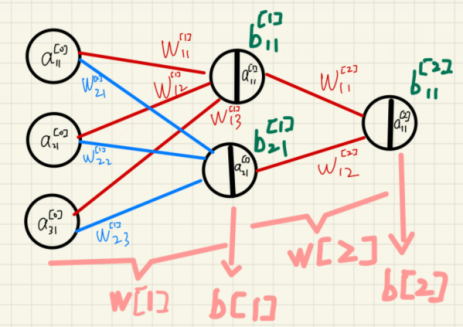
（注：字符右上角都是‘[n]’，其中n是0、1或2。）

关于输入与前向传播

  其中，输入是a[0]，维度为3*1；隐藏层输出为a[1]，维度为2*1；输出层输出为a[2]，维度1*1。（如下图）

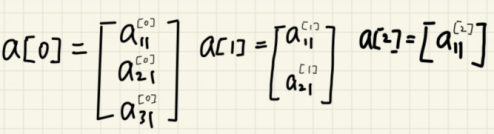
  如何从a[0]到达a[1]？从公式出发，计算过程是这样：

  这里激活函数在图中表示为将神经元一分为二的竖线，竖线左边是没有经过激活函数的值，右边是激活函数得到的值。

关于w和b

  其中，w[1]，w[2]具体如下：

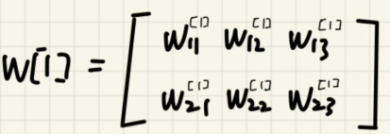
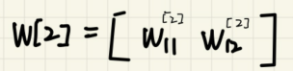
  b[1],b[2]具体如下：

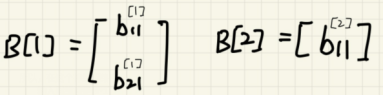
  所以，在这个神经网络中：

输入层维度是3*1；

隐藏层维度是2*1，隐藏层权重w[1]维度是2*3，隐藏层偏置b[1]维度是2*1；

输出层维度是1*1，输出层权重w[2]维度是1*2，输出层偏置b[2]维度是1*1。

  将上述维度投入前向传播的计算（计算公式上面有图已经给了），根据矩阵乘法的运算规则，可以正确地实现维度变换与验证。

小小实践验证一下

  接下来用pytorch构建一个网络进行验证，我们构建的目标网络还是这个：

代码：

from torch import nn
import torch.nn.functional as F

#初始化目标网络
class Net1(nn.Module):

    def __init__(self):

        super().__init__()

        self.hidden1=nn.Linear(3,2)#隐藏层，输入3个节点，输出2个节点

        self.out = nn.Linear(2,1)#输出层，输入2个节点，输出1个节点

#定义前向传播

    def forward(self,x):

        x = F.relu(self.hidden1(x))#隐层输出送入激活函数

        x = F.relu(self.out(x))#输出层输出送入激活函数

        return x

上面用pytorch定义好了网络，接下来输出一些信息。

net = Net1()
print(net)#直接输出这个网络结构

结果：

Net1(

  (hidden1): Linear(in_features=3, out_features=2, bias=True)

  (out): Linear(in_features=2, out_features=1, bias=True)

)

#打印一下具体参数信息
for name,parameter in net.named_parameters():
    print(name,parameter,parameter.size())

结果：

hidden1.weight Parameter containing:（隐层权重w[1]，维度2*3）

tensor([[-0.5633, -0.3537,  0.1340],

        [-0.4352,  0.0911,  0.0329]], requires_grad=True) torch.Size([2, 3])

hidden1.bias Parameter containing:（隐层偏置b[1]，维度2*1）

tensor([0.2649, 0.5501], requires_grad=True) torch.Size([2])

out.weight Parameter containing:（输出层权重w[2]，维度1*2）

tensor([[ 0.0372, -0.4675]], requires_grad=True) torch.Size([1, 2])

out.bias Parameter containing:（输出层偏置b[2]，维度1*1）

tensor([-0.6575], requires_grad=True) torch.Size([1])

  上面的例子只有一个隐层，其实算是一个比较特殊的网络了。

  下面再给一个具有两个隐层的网络的例子，同样的代码，自行观查一下输出，就可以更好地体会了。（这个运行结果就不贴了，因为神经元和参数太多，贴出来会很冗余。可以自己跑一下看看结果，其原理与上面的例子一模一样，就不再赘述了。）

from torch import nn

import torch.nn.functional as F

class Net1(nn.Module):

    def __init__(self):

        super().__init__()

        self.hidden1=nn.Linear(784,128)#第一个隐层

        self.hidden2=nn.Linear(128,256)#第二个隐层

        self.out = nn.Linear(256,1) #输出层

    def forward(self,x):

        x = F.relu(self.hidden1(x))

        x = F.relu(self.hidden2(x))

        x = self.out(x)

        return x

net = Net1()

print(net)

for name,parameter in net.named_parameters():

    print(name,parameter,parameter.size())

  好了，这篇文章整理了一下神经网络中层与层之间的权重矩阵w包括偏置b的维度，以及它们是如何参与前向传播运算的。整理一下就清楚多了~

最后

以上就是鲤鱼蜜蜂为你收集整理的神经网络前向传播 w的维度与含义的全部内容，希望文章能够帮你解决神经网络前向传播 w的维度与含义所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。