TensorFlow可变学习率及不同初始学习率对网络影响的比较

TensorFlow中的learning_rate_decay.py文件中查看更多

指数衰减

def exponential_decay(learning_rate, global_step, decay_steps, decay_rate,
                      staircase=False, name=None)

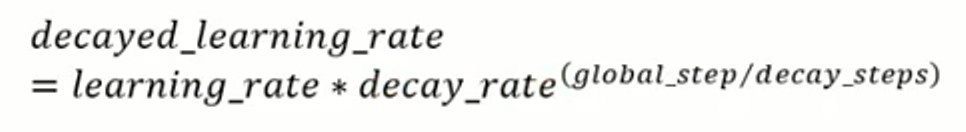
global_step是当前的步数，decay_steps是总共需要多少步下降到l_r*d_r的地方
staircase为True时，global_step/decay_steps是整数除法，阶梯状下降
learning_rate每隔decay_step步下降

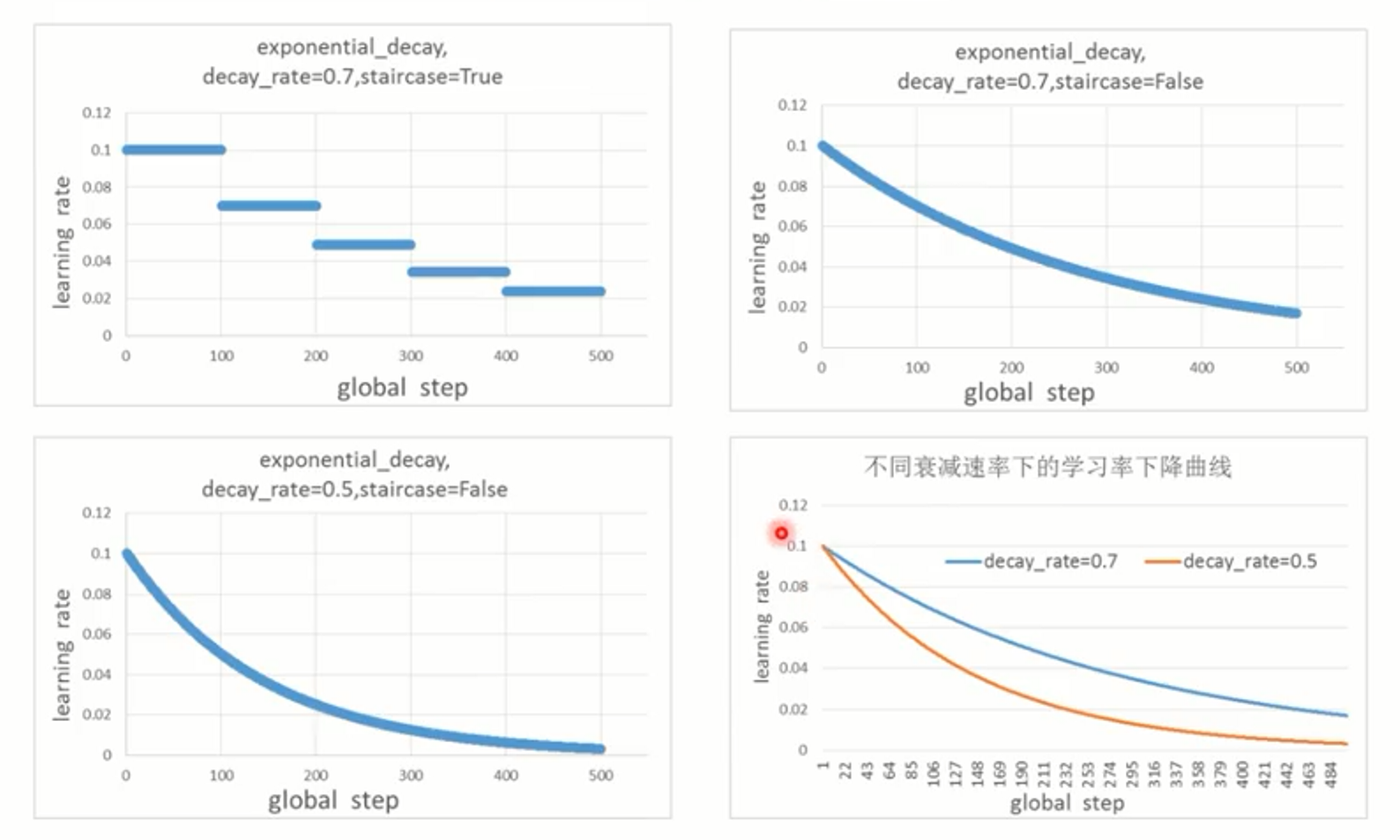
decay_rate越小，下降越快

global_step = tf.Variable(0, trainable=False)
starter_learning_rate = 0.1
learning_rate = tf.train.exponential_decay(starter_learning_rate, global_step=global_step, decay_steps=10000,
                                           decay_rate=0.96, staircase=True)
                                           
learning_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)

多项式衰减

def polynomial_decay(learning_rate, global_step, decay_steps,
                     end_learning_rate=0.0001, power=1.0, cycle=False, name=None)

cycle为学习率下降后是否重新上升

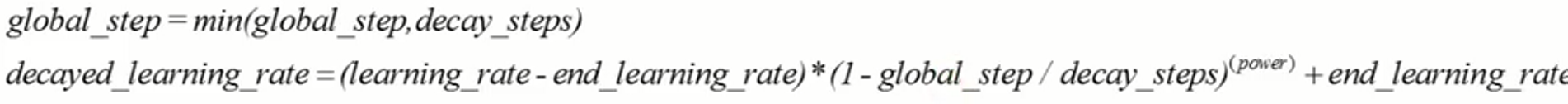
注意，这里：global_step = min(global_step, decay_steps)
learning_rate在decay_steps步内，到达end_learning_rate

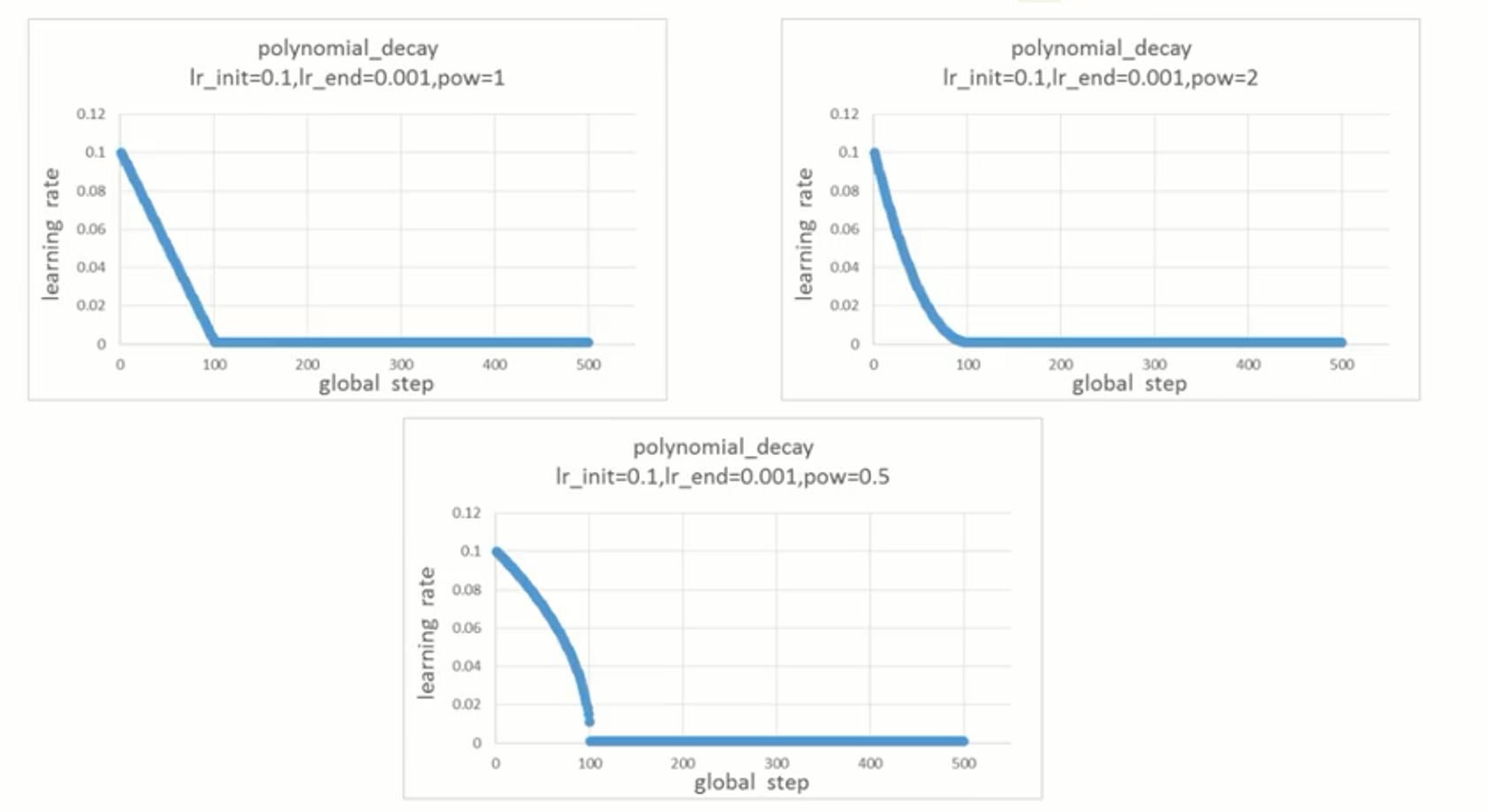
#decay from 0.1 to 0.01 in 10000 steps using sqrt(i.e. power=0.5)
global_step = tf.Variable(0, trainable=False)
starter_learning_rate = 0.1
end_learning_rate = 0.01
learning_rate = tf.train.polynomial_decay(starter_learning_rate, global_step=global_step, decay_steps=10000,
                                          end_learning_rate=end_learning_rate, power=0.5)
                                          
learning_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)

自然指数衰减

def natural_exp_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)

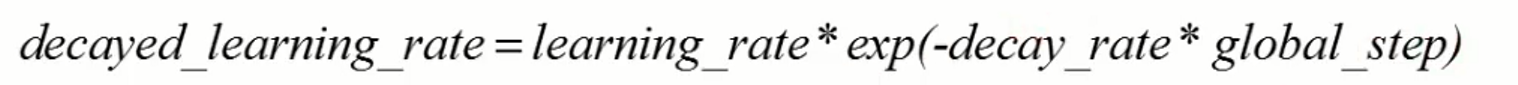
  # decay exponentially with a base of 0.96:
  global_step = tf.Variable(0, trainable=False)
  learning_rate = 0.1
  k = 0.5
  learning_rate = tf.train.exponential_time_decay(learning_rate, global_step, k)

  learning_step = (
      tf.train.GradientDescentOptimizer(learning_rate)
      .minimize(...my loss..., global_step=global_step)
  )

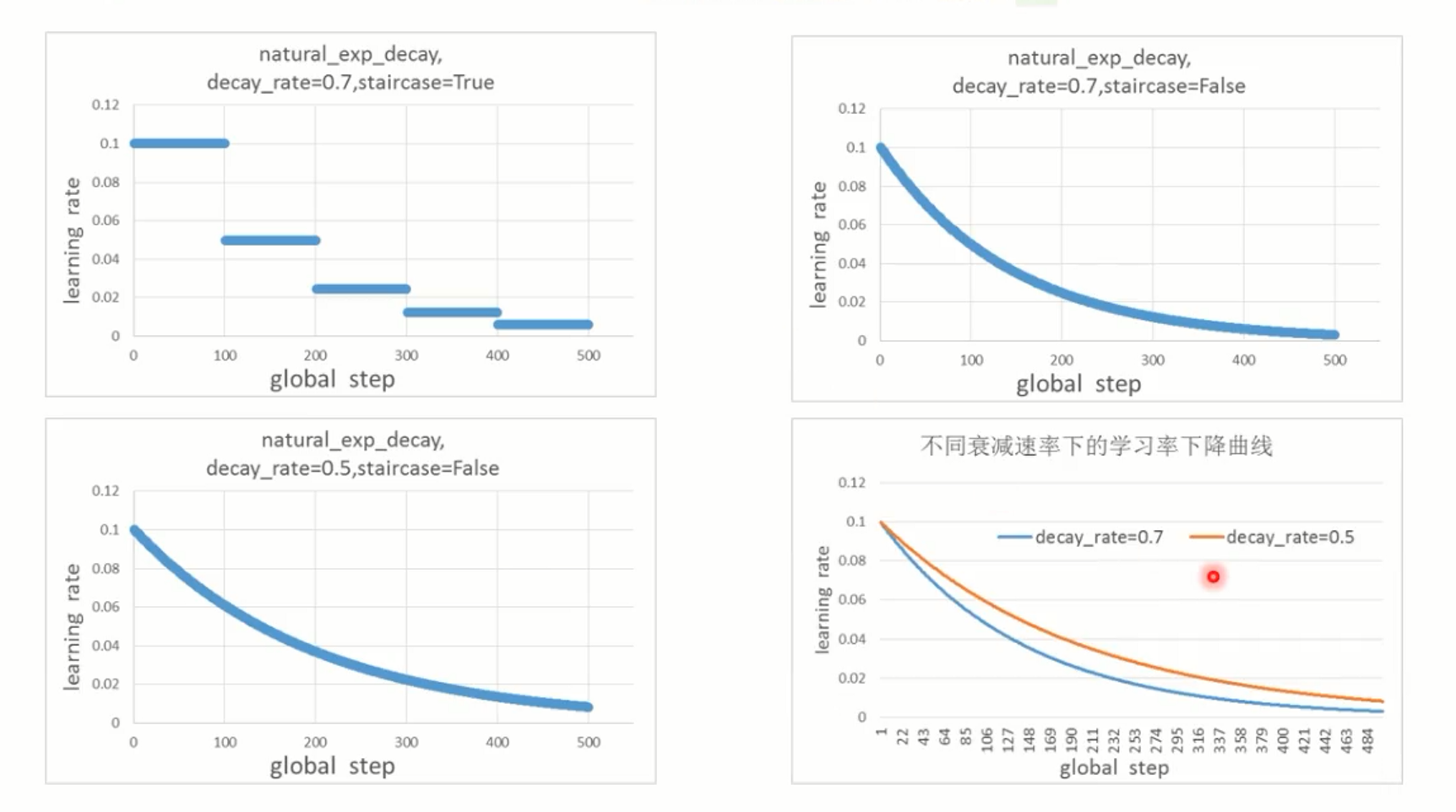
decay_rate越大，下降越快

时间翻转衰减

def inverse_time_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)

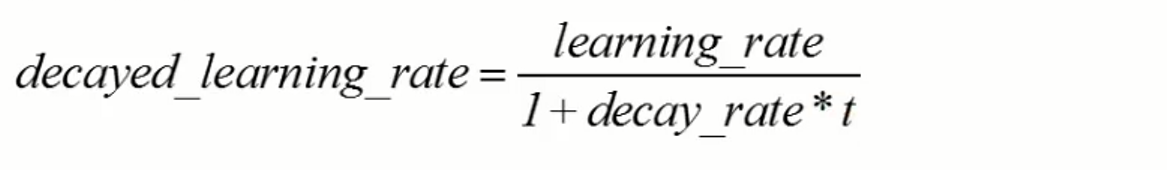
  # decay 1/t with a rate of 0.5:
  global_step = tf.Variable(0, trainable=False)
  learning_rate = 0.1
  decay_steps = 1.0
  decay_rate = 0.5
  learning_rate = tf.train.inverse_time_decay(learning_rate, global_step,
  decay_steps, decay_rate)

  learning_step = (
      tf.train.GradientDescentOptimizer(learning_rate)
      .minimize(...my loss..., global_step=global_step))

比较：

conv+relu+maxpool+linear_fc
下面是不同的初始学习率对网络影响的比较：




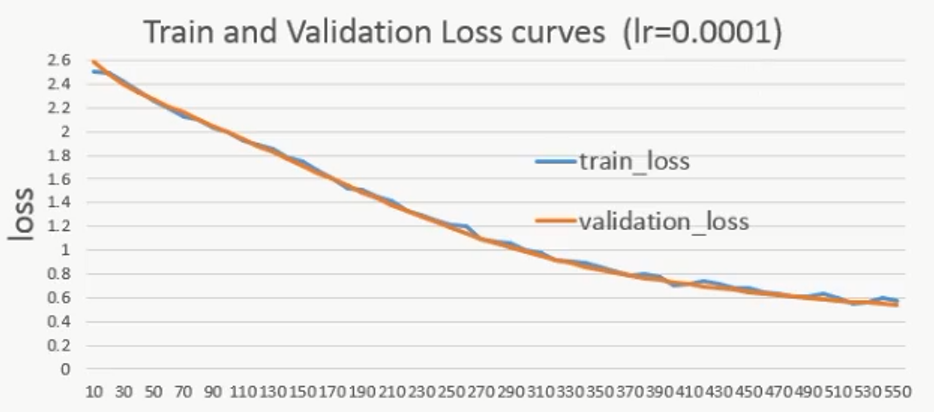
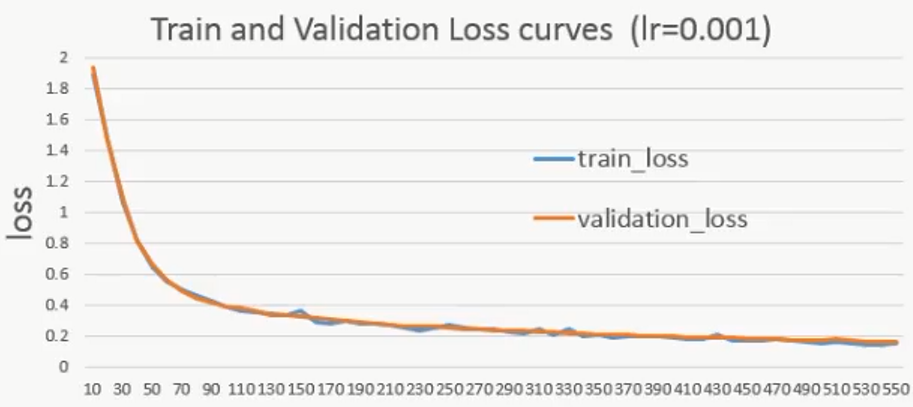
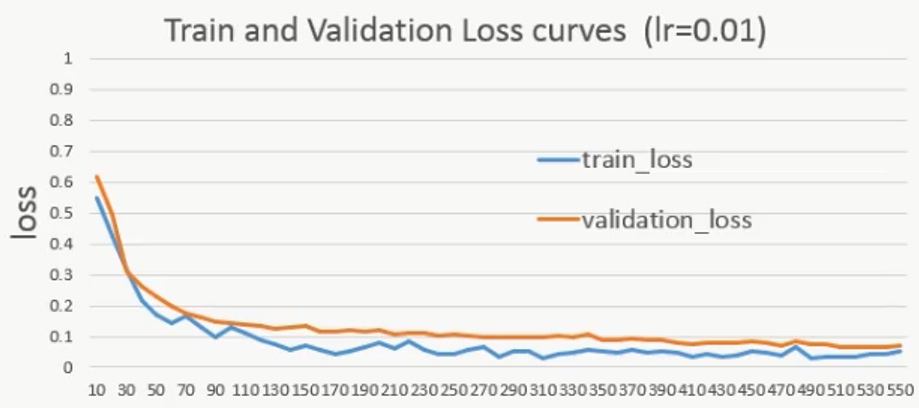
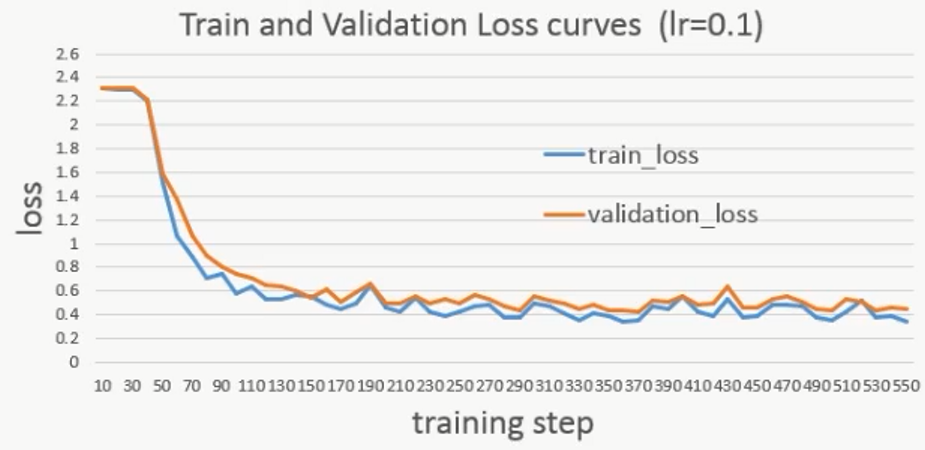
lr=0.1再跑一遍，发现初始损失变化较大：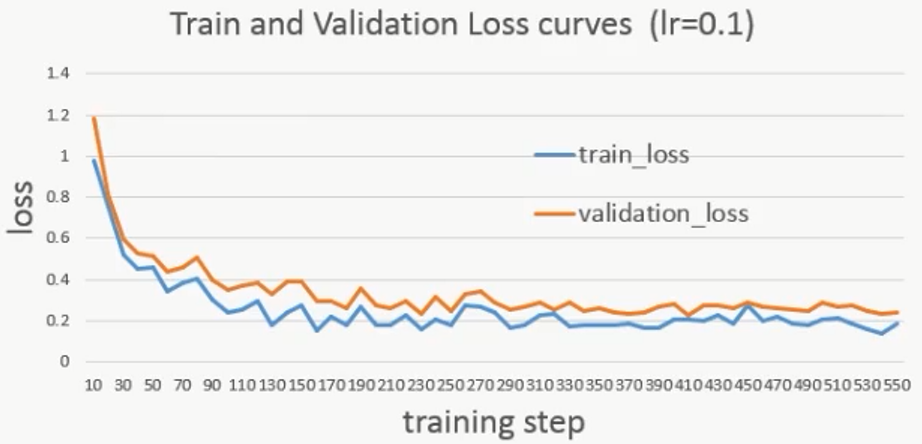
说明学习率越大，网络的表现越不稳定

最后

以上就是灵巧铃铛为你收集整理的TensorFlow可变学习率及不同初始学习率对网络影响的比较的全部内容，希望文章能够帮你解决TensorFlow可变学习率及不同初始学习率对网络影响的比较所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。