目录
- 全局最优与局部最优
- Hebb学习规则
- 常用的三种优化技巧
- 补充内容:快照集成
- 补充内容:神经网络剪枝
- 经典网络变种
- 小波神经网络
- RBF网络
- ART网络
- SOM网络
- Hopfield网络
- 基于遗传算法的网络
- 遗传算法
- 神经网络的概率式学习(比如基于遗传算法)
- 级联相关网络
- Elman网络与Jordan网络
- Boltzmann机,受限Boltzmann机,深度信念网络
- 扩展内容
- 关于神经网络等于黑箱
- 关于深度学习
全局最优与局部最优
Hebb学习规则
关于神经网络最早的优化方法应追溯到Hebb规则,赫布提出的Hebb学习规则为神经网络的学习算法奠定了基础,在此基础上,人们提出了各种学习规则和算法,以适应不同网络模型的需要。
Donald Hebb在1949年提出一种学习规则,用来描述神经元的行为是如何影响神经元之间的连接的,通俗的说,就是如果相链接的两个神经元同时被激活,显然我们可以认为这两个神经元之间的关系应该比较近,因此将这两个神经元之间连接的权值增加。这也是最早的原话"neurons that fire together, wire together"。用公式表示为: W i j ( t + 1 ) = W i j ( t ) + l r ⋅ x i x j W_{ij}(t+1)=W_{ij}(t)+lrcdot x_{i}x_{j} Wij(t+1)=Wij(t)+lr⋅xixj表明神经元 i , j i,j i,j之间的连接权重 W i j W_{ij} Wij由两者的输出 x i x_{i} xi和 x j x_{j} xj决定, l r lr lr为学习率。
可见,早期的学习方式是粗略的,使得网络不能加深不能变复杂,在反向传播算法提出后,使得神经网络的规模复杂化变成现实。
常用的三种优化技巧
神经网络的表现与训练数据集的标注存在误差,网络的训练过程可以看作是一个参数寻优过程。基于梯度的搜索是最广泛使用的参数寻优方法。我们从某些初始解开始,迭代寻找最优参数值。每次迭代中,我们先计算误差函数在当前点的梯度,然后根据梯度确定搜索方向。比如,由于负梯度方向是函数值下降最快的方向,因此梯度下降法就是沿着负梯度方向搜索最优解。
如果误差函数具有多个局部极小,则不能保证找到的解是全局最小,在现实任务中,我们通常尝试以下策略跳出局部极小,逼近全局最小(当然也有可能跳出全局最小)。
- 以多组不同参数初始化多个网络,取其中误差最小的解作为最终参数。这相当于从多个不同的起点开始搜索,最后我们在大量局部极小解中挑选最接近全局最小的解。
- 使用模拟退火思想,模拟退火在每一步都以一定概率接受比当前解更差的结果,这有助于跳出局部极小,在每次迭代过程中,接受次优解的概率应该随着时间的推移而逐渐降低,从而确保数值计算的稳定性。
- 使用随机梯度下降,随机梯度下降与标准梯度下降精确计算梯度不同,随机梯度下降在计算梯度时会引入更多随机性,这可以使模型随着后续样本的输入跳出局部极小,从而继续搜索;
从中可以看出,batch size不是越大越好,batch size小反而提高了训练的随机性,有利于跳出局部极小。
梯度下降Gradient Descent的三种变形形式:
- 批量梯度下降(Batch Gradient Descent):针对整个数据集,通过对所有样本计算误差求梯度;
- 小批量梯度下降(Mini-batch Gradient Descent):把数据分为若干小批,按批更新参数,一个批中的一组数据共同决定本次更新的方向;
- 随机梯度下降(Stochastic Gradient Descent):按样本更新参数,参数的更新方向由单个样本上计算的梯度决定;
梯度决定更新参数的方向,学习率决定参数更新的步长。
梯度下降的寻优路径通常是抖动的,共轭梯度法是把目标函数分成许多方向,然后按不同方向的目标分别求出极值再综合寻优,可以缓解抖动(沿着解空间的维度逐步构建最优解)。但共轭梯度更多是用于二次优化问题,在机器学习中更常用基于动量的梯度下降缓解GD的抖动。
目前的跳出局部极小策略都是启发式的(启发式算法:基于直观或经验构造的算法),理论上缺乏保障。
补充内容:快照集成
在常规bagging集成时,要同时训练多个网络,这造成了巨大的资源负担,并且每次的训练得到模型很可能并无实质性差异(参数相近),用大量相似的模型进行集成是没有意义的。
快照集成为bagging集成带来全新模式,快照集成(snapshot ensemble)可以描述为两点:
- 只需使用同一个训练过程:不同于一般的bagging集成,快照集成不需要重新训练模型,而是在同一个训练过程中,产生多个局部最优模型;
- 每个模型都具备多样性(参数各异):一般的bagging集成方法总是需要重新训练,只是为了保证模型的多样性,但其参数最后还是差异不明显,快照集成通过余弦退火调整学习率,让训练中的每个局部最优模型都具有实质性差异。
基于余弦退火调整的学习率如下图:
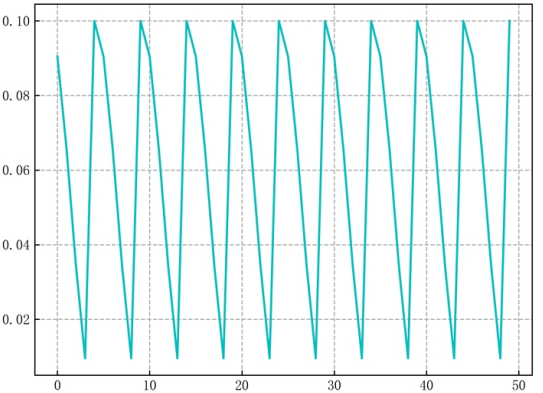
传统的训练过程中,学习率逐渐减小,所以模型逐渐找到局部最优点。这个过程中,因为一开始的学习率较大,模型快速往平坦的局部最优点移动。随着学习率逐渐减小,模型最终收敛到一个比较好的局部最优点。
由于余弦退火的调整,学习率急速下降,所以模型会迅速踏入局部最优点(不管是否陡峭),我们保存局部最优点的模型。快照集成中的快照因此得名。保存模型后,学习率重新恢复到一个较大值,跳出当前的局部最优点,并寻找新的局部最优点。由于学习率的大幅度变动,不同局部最优点的模型存在较大的差异(使局部最优模型具备多样性),所以bagging集成之后效果会更好。
补充内容:神经网络剪枝
神经网络剪枝可分为网络权重剪枝,神经元剪枝,滤波器剪枝,分层剪枝。
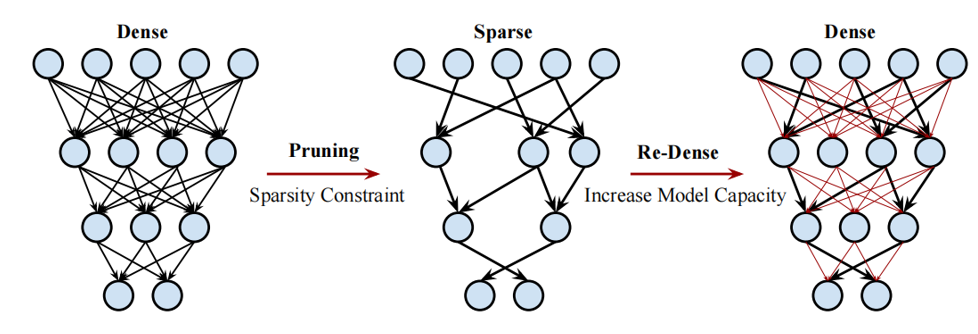
权重剪枝通过修剪网络中冗余的权重来压缩网络。在深度神经网络训练过程中,许多参数对于提升网络性能的贡献不大,将这些参数从网络中去除后对精度的影响也很小,同时可以显著地减少模型的存储、计算成本、能量和推理时间。主要做法是在学习权重的同时,也学习网络中每个连接的重要性。这种方法首先基于训练后的网络学习网络的拓扑结构以确定哪些神经元之间的连接重要,在剪枝时去除不重要的连接;然后重新训练网络,使得剩余的连接补偿被删除的部分。由于被剪枝的连接被从网络中永远删除,在训练时需要适当降低 dropout 率来适应这种变化。网络的剪枝与重建过程如下:
神经元剪枝与权重剪枝不同,神经元剪枝去除的是单个神经元,同时和该神经元相关的所有输入输出连接也将被删除。考虑下面情况:
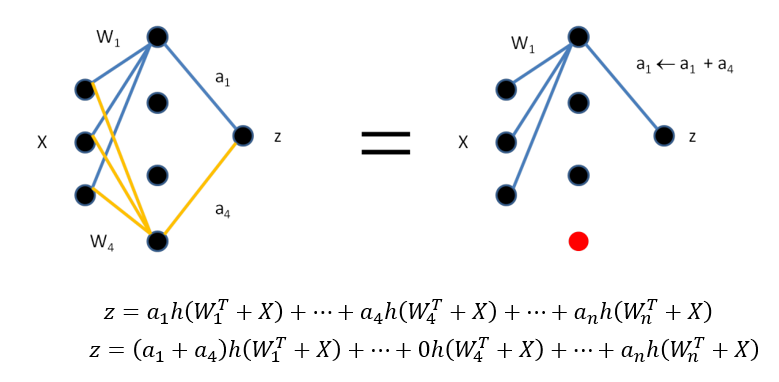
假设向量权重 W 1 , W 4 W_{1},W_{4} W1,W4是很相近的,那么它们对于激活值的影响只与输出层的标量权重 a 1 , a 4 a_{1},a_{4} a1,a4有关,从而得到上面式子的化简。
滤波器剪枝是对卷积网络的直观剪枝操作,虽然全连接网络的参数占比较大,但网络的主要计算集中在卷积层,滤波器剪枝对卷积层的参数进行排序,去除对精度影响小的卷积核,减少计算成本。
分层剪枝主要用于一些很深的网络,在网络的层级别进行剪枝,目的是在尽量不降低性能的前提下让模型结构更加紧凑,分层剪枝可以去除模型中冗余的网络层。
经典网络变种
小波神经网络
关于小波变换可以回顾算法栈中的其他算法-浅谈小波变换,小波神经网络(Wavelet Neural Network,WNN)是基于两层神经网络改变后得到的,它可以让信号分析具有一定解释性(用小波去解释隐层的表达),原因在于网络的隐层神经元的激活函数为小波基函数。WNN的拓扑结构如下:
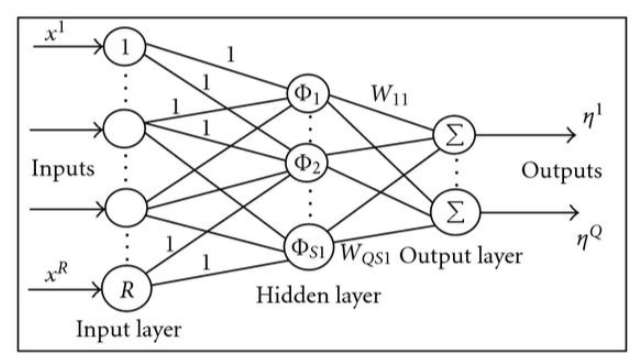
输入序列为:
x
i
,
(
i
=
1
,
2
,
,
.
.
.
,
R
)
x^{i},(i=1,2,,...,R)
xi,(i=1,2,,...,R)隐层输出表示为:
h
j
=
Φ
j
(
∑
i
=
1
R
W
i
j
x
i
+
b
j
a
j
)
,
(
j
=
1
,
2
,
.
.
.
,
S
1
)
h_{j}=Phi_{j}(frac{sum_{i=1}^{R}W_{ij}x^{i}+b_{j}}{a_{j}}),(j=1,2,...,S_{1})
hj=Φj(aj∑i=1RWijxi+bj),(j=1,2,...,S1)其中,
h
j
h_{j}
hj为隐层第
j
j
j个神经元的输出,
a
j
a_{j}
aj为伸缩因子,
b
j
b_{j}
bj为平移因子,
Φ
j
Phi_{j}
Φj为小波函数(通常选择Morlet小波函数):
Φ
(
x
)
=
c
o
s
(
1.75
x
)
e
−
x
2
2
Phi(x)=cos(1.75x)e^{-frac{x^{2}}{2}}
Φ(x)=cos(1.75x)e−2x2输出层的计算为普通全连接网络,激活函数为线性激活。
小波网络实际是一种引入人工限制的多层全连接网络,额外的限制(小波函数)可以帮助我们可解释地分析信号,小波网络的核心是通过梯度下降修正网络中的权重参数 W i j W_{ij} Wij与因子 a j , b j a_{j},b_{j} aj,bj,使网络输出符合构造的期望。
RBF网络
径向基函数网络是一种单隐层前馈神经网络,它使用径向基函数作为隐层神经元的激活函数,而输出层则是对隐层神经元输出的线性组合。假设输入为 d d d维向量 x x x,输出为实数,则RBF网络可以表示为: ϕ ( x ) = ∑ i = 1 q w i ρ ( x , c i ) ∈ R phi(x)=sum_{i=1}^{q}w_{i}rho(x,c_{i})in R ϕ(x)=i=1∑qwiρ(x,ci)∈R其中, q q q为隐层神经元的数量, c i , w i c_{i},w_{i} ci,wi分别为第 i i i个隐层神经元所对应的中心和权重, ρ rho ρ是径向基函数(沿着径向对称的标量函数),通常定义为样本 x x x到数据中心 c i c_{i} ci之间欧氏距离的单调函数,常用的高斯径向基函数为: ρ ( x , c i ) = e − β i ∣ ∣ x − c i ∣ ∣ 2 ∈ R rho(x,c_{i})=e^{-beta_{i}||x-c_{i}||^{2}}in R ρ(x,ci)=e−βi∣∣x−ci∣∣2∈R已有证明,具有足够多隐层神经元的径向基函数网络能以任意精度逼近任意连续函数。
通常,使用两步骤训练RBF网络:
- 确定神经元中心 c i c_{i} ci,常用的方法是随机采样或聚类;
- 反向传播更新参数 w i , β i w_{i},beta_{i} wi,βi。
ART网络
竞争学习(competitive learning)是一种无监督学习策略,网络某一层的神经元相互竞争,仅允许一个神经元被激活,其他神经元则被抑制。
ART网络(Adaptive Resonance Theory,自适应谐振理论)是竞争学习的代表模型,该网络由比较层,识别层,识别阈值和重置模块构成。其中,比较层负责接收输入样本,进行线性变换得到输入向量,并传递给识别层。识别层的每个神经元对应一个模式(无监督学习中的某个类别),神经元数目可以在训练过程中动态增长从而增加新的模式。注意:识别层中每个神经元对应着一个向量,该向量是对应模式的代表向量。
在接收到比较层的输入信号后,识别层神经元之间相互竞争产生获胜神经元。
竞争的最简单方式为:计算输入向量与每个识别层神经元对应的模式向量之间的距离,距离最小者胜出。从这个规律看出,"度量"是无监督学习的一种普遍方法。
下一步进行比较:
- 谐振:如果输入向量与获胜神经元的模式向量之间的相似度大于识别阈值,则当前输入样本将被归为该模式向量所属的模式,同时更新比较层中的参数矩阵,使得以后在接收到相似输入样本时可以计算出更大的相似度,进而让该神经元更容易获胜。
- 自适应:如果相似度小于识别阈值,则重置模块在识别层中新增一个神经元,其模式向量就为输入向量。
显然,识别阈值对ART网络的性能有重要影响,当识别阈值较高时,输入样本会被分成较多,且细粒度的模式。如果识别阈值过低,则会得到较少的模式。
ART网络缓解了竞争学习中的"可塑性-稳定性矛盾"。可塑性是:网络要具有学习新知识的能力。稳定性是:学习新知识时需要保留对旧知识的记忆。通常,如果对常规网络进行训练,当更换数据集后,旧知识会被新知识覆盖(这被称为灾难性遗忘)。而ART则可以轻松实现增量学习或在线学习。
增量学习是指在学到模型后,继续接收训练样例,仅使用新样例进行更新,不再遍历先前的整个数据集。由于不再考虑原数据集上的损失,增量学习面临着灾难性遗忘问题。
在线学习是增量学习的特例,在线学习是batch size=1的增量学习。
SOM网络
自组织映射网络(Self-Organizing Map Networks)也是一种竞争学习的无监督模型。它可以将高维输入数据映射到低维空间(通常为二维),同时保持输入数据在高维空间的拓扑结构(将高维空间中相似的样本点映射到网络输出层中的邻近神经元);
SOM网络框架如下:
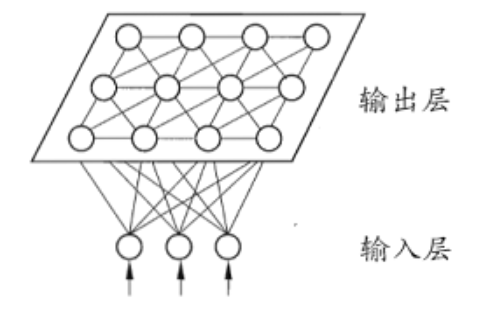
SOM网络中的输出层神经元以矩阵方式排列在二维空间中,每个神经元都拥有一个权向量,网络在接收输入向量后,将会确定输出层的获胜神经元,它决定了该输入向量在低维空间中的位置。SOM的训练目标就是为每个输出层神经元找到合适的权向量,以达到保持拓扑结构的目的。
SOM的训练过程为:
- 接收到一个训练样本,每个输出层神经元计算该样本与自身携带的权向量之间的距离,距离最近的神经元成为竞争获胜者,称为最佳匹配单元(best matching unit);
- 最佳匹配单元与邻居神经元的权向量被更新,以使得这些权向量与当前输入样本的距离缩小,这个过程不断迭代直至权向量收敛。
Hopfield网络
霍普菲尔德神经网络(Hopfield neural network)是一种递归神经网络(回顾机器学习笔记第二十四课.循环神经网络RNN),由约翰·霍普菲尔德在1982年发明。Hopfield网络是一种结合存储系统和二元系统的神经网络。
霍普菲尔德网络的单元是二元的(binary),即这些单元只能接受两个不同的值,并且值取决于输入的大小是否达到阈值。Hopfield网络通常接受值为-1或1,也可以是0或者1。
一个有四个节点的Hopfield网络如下:
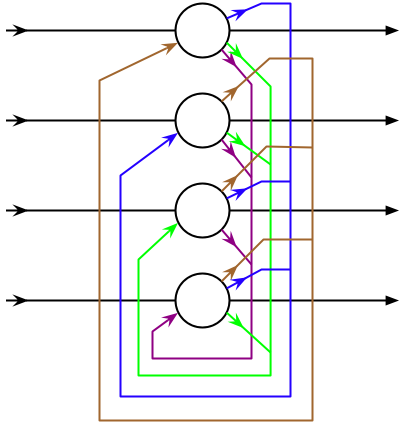
每一对Hopfield网络中的单元 i i i和 j j j都有一对一定权重的连接 w i j w_{ij} wij,因此,Hopfield网络可以被描述为一个完全无向图 G = ( V , f ) G=(V,f) G=(V,f),其中 V V V是神经元集合,网络的连接有以下特性:
- w i i = 0 w_{ii}=0 wii=0:没有神经元和自身相连;
- w i j = w j i w_{ij}=w_{ji} wij=wji:连接的权重对称;
权重对称是一个重要的特征,不对称的权重会引入周期性的噪声,妨碍模型收敛。
Hopfield网络的节点
i
i
i输出为
s
i
s_{i}
si:
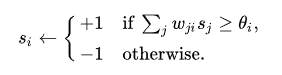
其中,
w
j
i
w_{ji}
wji是节点
j
j
j到节点
i
i
i的权重;
s
i
s_{i}
si为节点
i
i
i的值(状态state);
θ
i
theta_{i}
θi为节点
i
i
i的阈值,通常为0。
基于遗传算法的网络
遗传算法
遗传算法(Genetic Algorithm,GA)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。其主要特点是直接对结构对象进行操作,不存在函数可导,连续的限定。GA采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。
在遗传算法里,优化问题的解被称为个体,它表示为一个变量序列,叫做染色体或者基因串。染色体一般被表达为简单的字符串或数字串,不过也有其他的依赖于特殊问题的表示方法,这一过程称为编码。首先,算法随机生成一定数量的个体,有时候操作者也可以对这个随机产生过程进行干预,以提高初始种群的质量。
在每一代中,每一个个体都被评价, 并通过计算适应度函数得到一个适应度数值。种群中的个体被按照适应度排序,适应度高的 在前面。下一步产生下一代个体并组成种群。这个过程是通过选择和繁殖完成的,其中繁殖包括交配(crossover,交叉操作)和突变(mutation)。
选择是根据新个体的适应度进行的,但并不意味着完全以适应度高低作为导向,因为单纯选择适应度高的个体将可能导致算法快速收敛到局部最优解而非全局最优解,我们称之为早熟。遗传算法依据原则:适应度越高,被选择的机会越高,而适应度低的,被选择的机会就低。初始的数据可以通过这样的选择过程组成一个相对优化的群体。
被选择的个体进入交配过程。一般的遗传算法都有一个交配概率(又称为交叉概率),范围一般是 0.6~1,这个交配概率反映两个被选中的个体进行交配的概率。例如,交配概率为 0.8,则 80% 的"夫妻"会生育后代。每两个个体通过交配产生两个新个体,代替原来的"旧"个体,而不交配的个体则保持不变。交配父母的染色体相互交换,从而产生两个新的染色体,第一个个体前半段是父亲的染色体,后半段是母亲的,第二个个体则正好相反。不过这里的半段并不是真正的一半,这个位置叫做交配点,也是随机产生的,可以是染色体的任意位置。
再下一步是突变,通过突变产生新的"子"个体。遗传算法有一个固定的突变常数(又称为变异概率),通常是 0.1 或者更小,这代表变异发生的概率。根据这个概率,新个体的染色体随机突变,通常就是改变染色体的一个字节(0 变到 1,或者 1 变到 0)。经过这一系列的过程(选择、交配和突变),产生的新一代个体不同于初始的一代,并一代代向增加整体适应度的方向发展。
神经网络的概率式学习(比如基于遗传算法)
遗传算法在神经网络中的应用主要反映在两个方面: 网络的学习,网络的结构设计。
- 对于网络学习:用遗传算法对神经网络学习规则实现自动优化,从而提高学习速率。对于网络权重的优化,遗传算法的隐含并行性可以提高权重的优化速度;
换言之,我们直接将网络的参数编码,用遗传算法去优化参数。 - 网络的结构设计:把神经网络用二进制编码序列表示,适应度函数根据任务设计,用遗传算法优化染色体能帮助我们得到一个优良的网络结构。
级联相关网络
一般的神经网络通常假设网络结构是事先固定的,训练的目的是通过样本确定合适的连接权重 W W W和激活阈值即偏置 b b b。与此不同,结构自适应网络将网络结构也作为学习的目标,并希望能在训练中找到更合适的网络结构与参数。级联相关网络(Casecade-Correlation)是结构自适应网络的代表。
结构自适应网络也被称为"构造性"网络
前面的ART网络由于识别层神经元数目可以在训练中动态增长,因此ART网络也是结构自适应网络
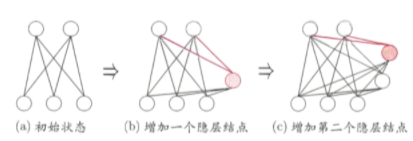
在上图中,展示了级联相关网络的训练过程,新的隐节点加入时,红色连接权重通过最大化新节点的输出与网络误差之间的相关性进行训练。
级联相关网络有两个主要部分:
- 级联:级联指的是建立层级之间的连接。在开始训练时,网络只有输入层和输出层,处于最小的拓扑结构。随着训练的进行,如上图所示,新的隐层神经元逐渐加入,从而创建层级结构,当新的隐层神经元加入时,其输入端连接权重是冻结的。
- 相关:通过最大化新神经元的输出与网络误差之间的相关性来训练相关的参数。
与一般的前馈神经网络相比,级联相关网络无需设置网络层数,隐层神经元个数,且训练速度较快。
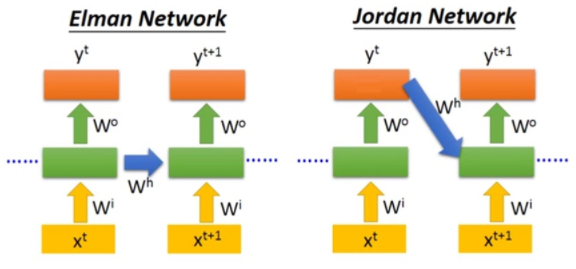
Elman网络与Jordan网络
Elman网络即循环神经网络RNN,网络的训练需要使用推广的BP算法(BPTT)。Elman网络与Jordan网络都属于递归神经网络,两者结构如下:
Boltzmann机,受限Boltzmann机,深度信念网络
神经网络中有一类模型是为网络状态定义一个"能量",能量最小化时,网络达到理想状态,网络的训练就是最小化能量函数(可以类比无向概率图中的条件随机场)。玻尔兹曼机就是一种基于能量的模型,常见结构如下图a所示:
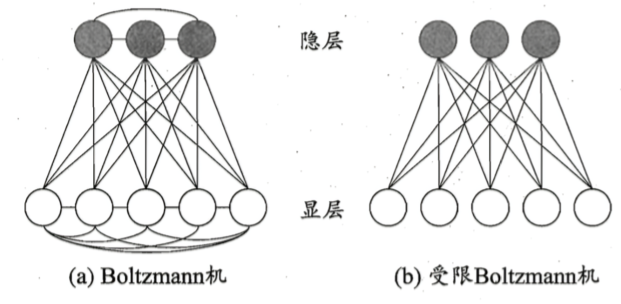
其神经元分为两层(可以看出,Boltzmann机其实是一种递归神经网络)。显层用于表示数据的输入与输出。隐层则用于表示数据的内在表达。Boltzmann机中的神经元都是布尔型的,只能取0,1两种状态,状态1表示激活,状态0表示抑制。令向量
s
∈
{
0
,
1
}
n
textbf{s}inleft{0,1right}^{n}
s∈{0,1}n表示
n
n
n个神经元的状态,
w
i
j
w_{ij}
wij表示神经元
i
i
i与
j
j
j之间的连接权,
θ
i
theta_{i}
θi表示神经元
i
i
i的激活阈值(偏置),则状态向量
s
textbf{s}
s所对应的Boltzmann能量定义为:
E
(
s
)
=
−
∑
i
=
1
n
−
1
∑
j
=
i
+
1
n
w
i
j
s
i
s
j
−
∑
i
=
1
n
θ
i
s
i
E(textbf{s})=-sum_{i=1}^{n-1}sum_{j=i+1}^{n}w_{ij}s_{i}s_{j}-sum_{i=1}^{n}theta_{i}s_{i}
E(s)=−i=1∑n−1j=i+1∑nwijsisj−i=1∑nθisi如果网络中的神经元以任意不依赖于输入值的顺序更新,则网络最终将达到boltzmann分布(即一种平稳分布,稳态),此时状态向量
s
textbf{s}
s出现的概率将仅由其能量于所有可能状态向量的能量确定:
P
(
s
)
=
e
−
E
(
s
)
∑
t
e
−
E
(
t
)
P(textbf{s})=frac{e^{-E(textbf{s})}}{sum_{textbf{t}}e^{-E(textbf{t})}}
P(s)=∑te−E(t)e−E(s)Boltzmann机的训练过程就是将每个训练样本视为一个状态向量,使其出现的概率尽可能大。
标准的Boltzmann机是一个完全图,训练网络的复杂度很高。实际情况中常采用受限Boltzmann机(RBM),如上图b所示。RBM仅保留显层于隐层之间的连接,从而将完全图简化成二分图。
RBM常用对比散度(Contrastive Divergence,CD)进行训练。假设网络中有 d d d个显层神经元和 q q q个隐层神经元,令 v textbf{v} v和 h textbf{h} h去分别表示显层和隐层的状态向量,则由于同一层内不存在连接,可以得到: P ( v ∣ h ) = ∏ i = 1 d P ( v i ∣ h ) P(textbf{v}|textbf{h})=prod_{i=1}^{d}P(v_{i}|textbf{h}) P(v∣h)=i=1∏dP(vi∣h) P ( h ∣ v ) = ∏ j = 1 q P ( h j ∣ v ) P(textbf{h}|textbf{v})=prod_{j=1}^{q}P(h_{j}|textbf{v}) P(h∣v)=j=1∏qP(hj∣v)CD算法对每个训练样本 v textbf{v} v,先根据 P ( h ∣ v ) = ∏ j = 1 q P ( h j ∣ v ) P(textbf{h}|textbf{v})=prod_{j=1}^{q}P(h_{j}|textbf{v}) P(h∣v)=∏j=1qP(hj∣v)计算隐层神经元状态的概率分布,然后根据这个概率分布,从中采样出 h textbf{h} h,根据 P ( v ∣ h ) = ∏ i = 1 d P ( v i ∣ h ) P(textbf{v}|textbf{h})=prod_{i=1}^{d}P(v_{i}|textbf{h}) P(v∣h)=∏i=1dP(vi∣h)得到显层神经元的概率分布,采样得到 v ′ textbf{v}' v′,再根据 v ′ textbf{v}' v′得到 h ′ textbf{h}' h′,这类似于是一个自编码器过程,权重更新的计算为: Δ w = l r ( v h T − v ′ h ′ T ) Delta w=lr(textbf{v}textbf{h}^{T}-textbf{v}'textbf{h}'^{T}) Δw=lr(vhT−v′h′T)对于深度信念网络(Deep belief network,DBN),每层都是一个受限玻尔兹曼机,整个网络可视为由若干RBM堆叠得到。通常使用无监督逐层训练策略:
- 首先训练第一层,这是关于训练样本的RBM模型,可以按照标准的RBM方法训练;
- 然后,将第一层预训练好的隐层节点视为第二层的显层节点,对第二层进行训练;
- 以此类推,对多个层进行训练,在训练结束后,通过BP算法对整个网络进行有监督的微调。
扩展内容
关于神经网络等于黑箱
在控制科学中,神经网络的可解释性表现为可以找到传递函数等价的网络,不能找到传递函数的网络将会被视为"黑箱"。神经网络重在基于数据驱动的拟合,不容易实现解析式拟合。因而大部分人认为这是黑箱。
关于深度学习
深度学习发展自多层神经网络,多层网络在训练时更加困难,误差在多个层之间传播,往往会发散而不能让网络收敛到稳定状态。Highway网络通过建立直接的级联,促进梯度的传播,有利于网络的收敛,ResNet即是优秀的代表。
在过去的机器学习中,描述样本的特征通常需要人类专家设计,这被称为特征工程(feature engineering),然而,特征的好坏对泛化性能有至关重要的影响,人类专家设计特征也是困难的事情,深度学习的特征抽象能力改变了这一现象。深度学习也被称为特征学习,特征学习可以通过机器自动提取特征,这让人工智能得到进一步发展。
最后
以上就是知性画笔最近收集整理的关于第三十三课.一些经典的优化策略与神经网络变种全局最优与局部最优经典网络变种扩展内容的全部内容,更多相关第三十三课.一些经典内容请搜索靠谱客的其他文章。








发表评论 取消回复