深度学习入门基于Python的理论与实现_第三章_神经网络前言1. 从感知机到神经网络衔接2. 激活函数3. 多维数组的运算4. 3层神经网络的实现5. 输出层的设计6. 手写数字识别7. 小结

前言

• 对于第二章学过的感知机来说，它(理论上)能够表示可以进行复杂处理的计算机，但确定合适的、能够符合预期的输入与输出的权重(偏置和权重)的工作还是由人工来进行的。
• 神经网络解决了上面所说的问题，具体来说，神经网络可以自动地从数据中学习到合适的权重参数。
• 本章中，先介绍神经网络的概要，然后重点关注神经网络进行识别时的处理。
• 第四章，将讲解神经网络如何从数据中学习权重参数。

1. 从感知机到神经网络

1.1 神经网络的例子

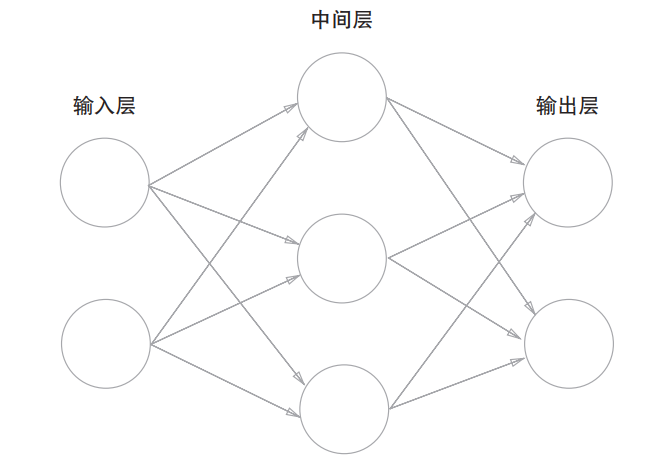
• 下图为神经网络的一个例子，包括输入层、中间层和输出层，其中中间层有时也称为隐藏层。“隐藏”意为隐藏层的神经元是肉眼看不见的。
• 另外，本书约定，从输入层到输出层依次称为第0层、第1层、第2层，这是为了方便后面基于Python来实现。
• 下图中的网络为2层网络，因为实质上只有2层神经元(输入层、隐藏层、输出层的总数减去1)有权重。
  

1.2 复习感知机

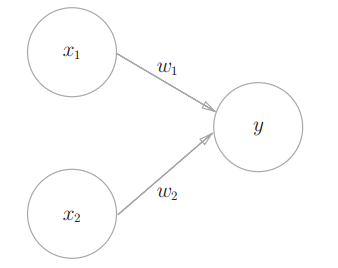
• 下图的感知机接收x₁和x₂两个输入信号，输出信号y。
  

• 其数学表达式如式(3.1)所示。其中，b被称为偏置，用于控制神经元被激活的容易程度；w₁和w₂被称为权重，用来表示各个信号的权重，用于控制各个信号的重要性。
  

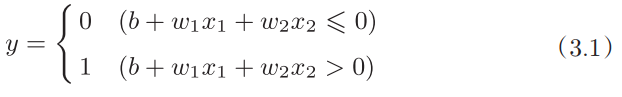
• 上图中，偏置b并没有表示在感知机的图中，如果要明确的表示出b，可以像下图这样做。
  
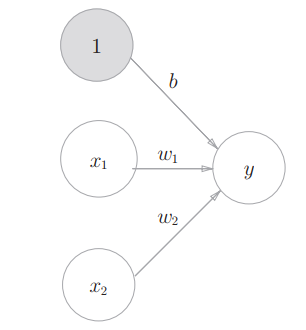
  上图中的感知机将x₁、x₂、1三个信号作为神经元的输入，将其和各自的权重相乘后，传送至下一个神经元。在下一个神经元中，计算这些加权信号的总和，如果总和超过0，则输出1，否则输出0。

• 现在我们将式(3.1)改写成更简洁的形式：引入一个新的函数h(x)(超过0输出1，否则输出0)。
  
  
  式(3.2)中，输入信号的总和会被函数h(x)转换，转换后的值就是输出y。

1.3 激活函数登场

• 式(3.3)中的h(x)函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数。“激活函数”的作用在于决定如何来激活输入信号的总和。
• 现在将式(3.2)进一步改写：先计算输入信号的加权总和，然后用激活函数转换这一总和：
  首先，式(3.4)计算加权输入信号和偏置的总和，记为a，然后式(3.5)用h()函数将a转换为输出y。
  
• 之前的神经元都是用○表示的，如果要在图中明确表示出式(3.4)和式(3.5)，可以像下图这样做。
  
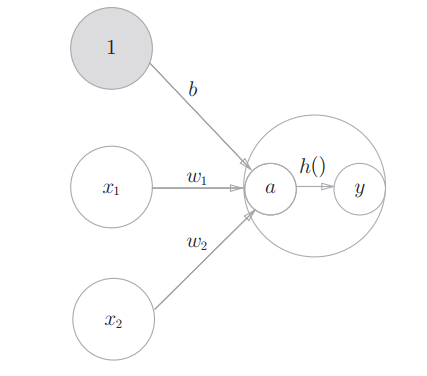
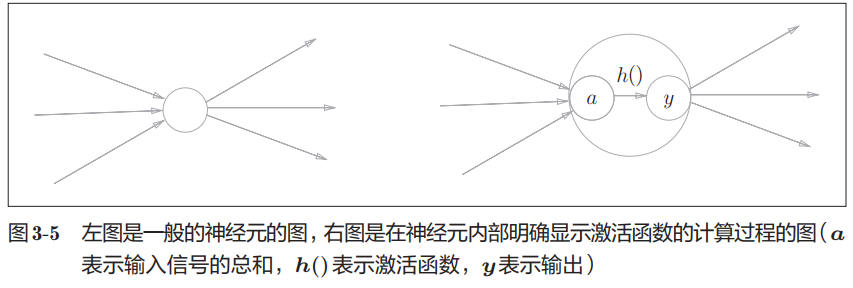
• 通常如下面的左图所示，神经元用○表示。本书中，在可以明确神经网络的动作的情况下，将在图中明确显示激活函数的计算过程，如右图所示。
  

衔接

本章的第二节将介绍激活函数，激活函数是连接感知机和神经网络的桥梁。

本书在使用感知机一词时，没有严格统一它所指的算法。一般来说：

• 朴素感知机是指单层网络，指的是激活函数使用了阶跃函数的模型。
• 多层感知机是指神经网络，指的是激活函数使用了sigmoid函数等平滑的激活函数的多层网络。

2. 激活函数

• 式(3.3)表示的激活函数以阈值为界，一旦输入超过阈值，就切换输出，这样的函数称为阶跃函数。因此，可以说感知机中使用了阶跃函数作为激活函数。
• 那么如果感知机使用其他函数作为激活函数的话会怎么样呢？事实上，如果将激活函数从阶跃函数换成其他函数，就可以进入神经网络的世界了。
• 接下来介绍一下神经网络使用的激活函数。

2.1 sigmoid函数

• 神经网络中经常使用的一个激活函数就是式(3.6)表示的sigmoid函数(sigmoid function)。式中的exp(-x)表示e^x。
  
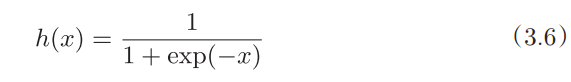
• 神经网络中用sigmoid函数作为激活函数，进行信号的转换，转换后的信号被传送给下一个神经元。
• 实际上，感知机和神经网络的主要区别就在于激活函数。其他方面，比如神经元的多层连接的构造、信号的传递方法等，基本上和感知机是一样的。

2.2 阶跃函数的实现

• 利用Python实现阶跃函数。

import numpy as np

def step_function(x):
    y = x > 0
    return y.astype(np.int)


if __name__ == "__main__":
    a = step_function(np.array([-1, -2, 2, 3, 0, -5]))
    print(a)

[0 0 1 1 0 0]

• 对于y = x > 0这行代码，根据双目运算符的优先级，先进行逻辑关系运算，即先比较x与0的大小，这里x既可以是一个数，也可以是一个NumPy数组，我们输入的是NumPy数组，在数组进行逻辑关系运算时，数组的各个元素都会进行不等号的逻辑运算，生成一个布尔型数组，然后将这个布尔型数组赋值给y。
• 由于我们需要阶跃函数最终输出的是int型数据而不是bool型数据，因此我们需要把数组y的元素类型从bool类型转换为int类型。这就要利用到NumPy数组的astype()方法，利用astype()方法可以转换NumPy数组的数据类型，因此我们需要将y从bool类型转换为int类型就要将astype()方法中的参数设置为np.int。如此一来，True就转换为1，False就转换为0。

2.3 阶跃函数的图形

• 利用Python来绘制刚刚定义的函数step_function()的图形。

import numpy as np
import matplotlib.pyplot as plt

def step_function(x):
    return np.array(x > 0, dtype=np.int)

if __name__ == "__main__":
    x = np.arange(-5.0, 5.0, 0.1)
    y = step_function(x)
    plt.plot(x, y)
    plt.ylim(-0.1, 1.1) # 指定y轴的范围
    plt.show()

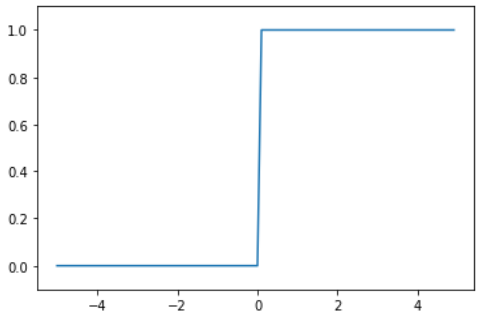
• 如上图所示，阶跃函数以0为界，输出从0切换为1，它的值呈阶梯式变化，所以称为阶跃函数。

2.4 sigmoid函数的实现

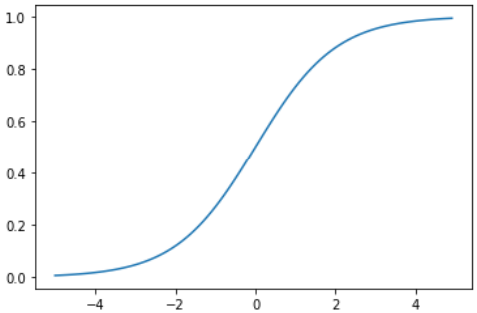
• 利用Python来实现sigmoid函数，并绘制出sigmoid函数的图形。

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

if __name__ == "__main__":
    x = np.arange(-5.0, 5.0, 0.1)
    y = sigmoid(x)
    plt.plot(x, y)
    plt.show()

2.5 sigmoid函数和阶跃函数的比较

• 首先利用Python绘制出sigmoid和阶跃函数的图形。

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def step_function(x):
    return np.array(x > 0, dtype=np.int)

if __name__ == "__main__":
    x = np.arange(-5.0, 5.0, 0.1)
    y1 = sigmoid(x)
    y2 = step_function(x)
    plt.plot(x, y1, label="sigmoid")
    plt.plot(x, y2, linestyle = "--", label="step_function")
    plt.xlabel("x")
    plt.ylabel("y")  
    plt.legend()
    plt.show()  

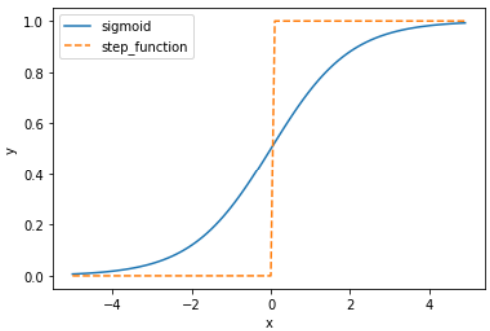
• 二者的不同点主要体现在：

1. 两个函数的平滑性不同。sigmoid是一条平滑的曲线，输出随着输入发生连续性的变化；阶跃函数以0为界，输出在0处发生急剧性的变化。sigmoid函数的平滑性对神经网络的学习具有重要意义。
2. 两个函数输出值的连续性不同。sigmoid函数可以输出0.731…0.880等实数；阶跃函数只能输出0或1。
   这也说明了：感知机中神经元之间流动的是0或1的二元信号，而神经网络中流动的是连续的实数信号。

• 二者的相同点主要体现在：

1. 两个函数的形状相似。即，当输入信号为重要信息时，阶跃函数和sigmoid函数都会输出较大的值；当输入信号为不重要的信息时，两者都输出较小的值。
2. 两个函数输出值在0到1之间。
3. 两个函数均为非线性函数。

2.6 非线性函数

输出值是输入值的常数倍的函数称为线性函数(h(x) = Cx，C为常数)。因此，线性函数是一条笔直的直线。
非线性函数指的是不像线性函数那样呈现出一条直线的函数。

• 神经网络的激活函数必须使用非线性函数。即，激活函数不能使用线性函数，因为使用线性函数的话，加深神经网络的层数就没有意义了。

• 线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。
  举个例子：首先，我们把线性函数h(x) = Cx作为激活函数，把y(x) = h(h(h(x)))的运算对应3层神经网络，这个运算等效于y(x) = c×c×c×x的乘法运算，但是同样的处理可以由y(x) = ax(a = c³)这一乘法运算(即没有隐藏层的神经网络)来表示。
• 如同上面的例子，使用线性函数的话，无法发挥多层网络带来的优势。

• 因此，为了发挥叠加层所带来的优势，激活函数必须使用非线性函数。

2.7 ReLU函数

• 在神经网络的发展历史上，sigmoid函数很早就开始用了，最近则主要使用ReLU(Rectified Linear Unit)函数(修正线性单元函数)
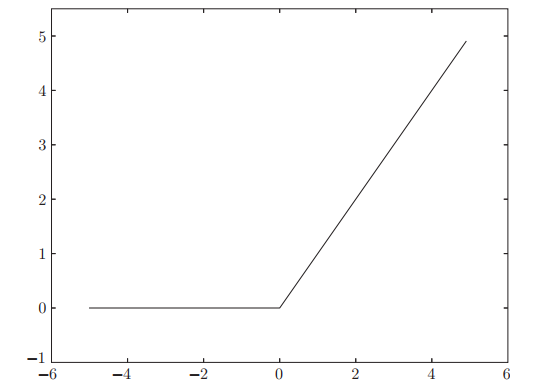
• ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。ReLU函数的表达式见式(3.7)。
  
• ReLU函数的图像见下图。
  
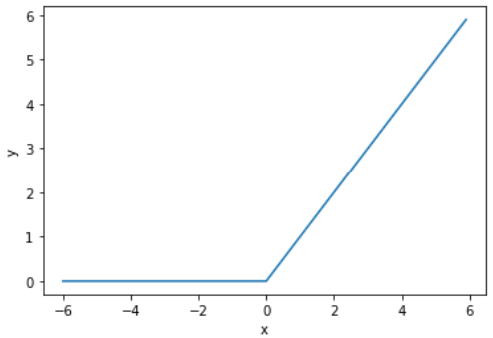
• 利用Python可实现ReLU函数，这里使用了NumPy的maximum函数，maximum函数会从输入的数值中选择较大的那个值进行输出。

import numpy as np
import matplotlib.pyplot as plt

def relu(x):
    return np.maximum(0, x)

if __name__ == '__main__':
    x = np.arange(-6.0, 6.0, 0.1)
    y = relu(x)
    plt.plot(x, y, label = 'relu')
    plt.xlabel("x")
    plt.ylabel("y")  
    plt.show()  

• 本章剩余部分的内容仍将使用sigmoid函数作为激活函数，但在本书的后半部分，将主要使用ReLU函数。

3. 多维数组的运算

3.1 多维数组

3.2 矩阵乘法

3.3 神经网络的内积

4. 3层神经网络的实现

4.1 符号确认

4.2 各层间信号传递的实现

4.3 代码实现小结

5. 输出层的设计

5.1 恒等函数和softmax函数

5.2 实现softmax函数时的注意事项

5.3 softmax函数的特征

5.4 输出层的神经元数量

6. 手写数字识别

6.1 MNIST数据集

6.2 神经网络的推理处理

6.3 批处理

7. 小结

最后

以上就是优秀吐司为你收集整理的深度学习入门基于Python的理论与实现_第三章_神经网络前言1. 从感知机到神经网络衔接2. 激活函数3. 多维数组的运算4. 3层神经网络的实现5. 输出层的设计6. 手写数字识别7. 小结的全部内容，希望文章能够帮你解决深度学习入门基于Python的理论与实现_第三章_神经网络前言1. 从感知机到神经网络衔接2. 激活函数3. 多维数组的运算4. 3层神经网络的实现5. 输出层的设计6. 手写数字识别7. 小结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。