深度学习入门基于Python的理论与实现_第二章_感知机(神经网络基础)前言1. 感知机是什么2. 简单逻辑电路3. 感知机的实现4. 感知机的局限性5. 多层感知机6. 从与非门到计算机7. 小结

前言

• 本章介绍感知机算法，感知机是由美国学者Frank Rosenblatt在1957年提出的，它是作为神经网络（深度学习）的起源的算法。
• 学习感知机的构造是学习通向神经网络和深度学习的一种重要思想。

1. 感知机是什么

• 感知机接收多个输入信号，输出一个信号。

• 感知机的信号只有1和0两种取值，0对应不传递信号，1对应传递信号。

• 下图为一个接收两个输入信号的感知机。其中x₁、x₂是输入信号，y是输出信号，w₁、w₂是权重(w是weight的首字母)。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时，会被乘以固定的权重，神经元会计算传送过来的信号的总和，只有当这个总和超过了某个阈值θ时，才会输出1。此过程也称为“神经元被激活”
  

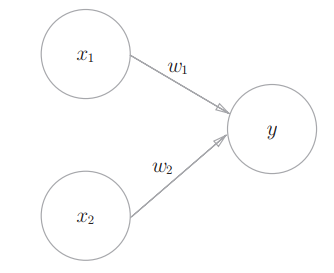
• 上述内容的数学表达式为：
  

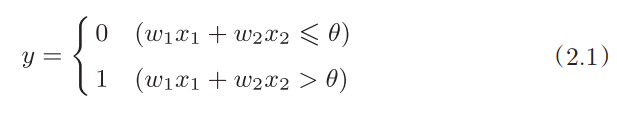
• 输入信号都有各自固定的权重，权重发挥着控制各个信号的重要性的作用，权重越大，对应该权重的信号的重要性就越高。

• 权重相当于电路里的电导。电导是描述某一种导体传输电流能力强弱程度，电导越大，通过的电流越大；在感知机中，权重越大，通过的信号就越大。

2. 简单逻辑电路

• 可以通过对参数设定不同的取值来实现不同的逻辑门功能。
  以上述的两输入的感知机为例：
  如(w₁, w₂, θ) = (0.5, 0.5, 0.7)，可实现与门(AND gate)的功能。
  如(w₁, w₂, θ) = (-0.5, -0.5, -0.7)，可实现与非门(NAND gate)的功能。
  如(w₁, w₂, θ) = (0.5, 0.5, 0.3)，可实现或门(OR gate)的功能
• 如上所示，与门、与非门、或门的感知机的构造是一样的，实际上，上述三个门电路只有参数(权重和阈值)的取值不同。也就是说，相同构造的感知机，只需通过适当地调整参数的值，就可以实现不同的功能。
• 从上面的分析我们可以看出，决定感知机参数的并不是计算机，而是我们人，我们通过逻辑真值表这种“训练数据”，人工考虑出参数的值。而机器学习就是将这个决定参数值的工作交给计算机自动进行。
  学习是确定合适的参数的过程，而人要做的是思考感知机的构造(模型)，并把训练数据交给计算机

3. 感知机的实现

3.1 简单的实现

• 通过Python来实现与门，首先定义一个接收参数为x1和x2的函数，再在函数内初始化参数w1、w2、theta，当输入的加权总和超过阈值时返回1，否则返回0。

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1 * w1 + x2 * w2
    if tmp <= theta:
        return 0
    elif tmp > theta:
        return 1
    
print(AND(0, 0))
print(AND(0, 1))
print(AND(1, 0))
print(AND(1, 1))

0
0
0
1

3.2 导入权重和偏置

• 考虑到之后的事，我们通过另外一种实现形式来实现与门：
  首先把式(2.1)的θ换成-b，于是就可以用式(2.2)来表示感知机的行为。式(2.2)中，b称为偏置(此处可以把永磁偏置和纯电磁偏置中的偏置给解释清楚)，w₁，w₂称为权重。
  感知机会计算输入信号和权重的乘积，然后加上偏置，如果这个值大于0则输出1，否则输出0。
  
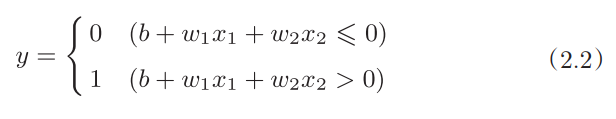
• 接下来，通过NumPy，按照式(2.2)来实现具有逻辑与功能的感知机：

import numpy as np

x = np.array([0, 1]) # 输入
w = np.array([0.5, 0.5]) # 权重
b = -0.7 # 偏置

print(np.sum(w * x) + b)

-0.19999999999999996

3.3 使用权重和偏置的实现

• 借助Python，使用权重和偏置来实现与门：
  与使用权重和阈值不同的是，这里把-θ命名为偏置b，需要注意的是，偏置和权重的作用是不同的。
  权重是控制输入信号的重要性的参数。
  偏置是调整神经元被激活的容易程度的参数。
• 根据上下文，有时也会将b、 w₁、 w₂这些参数统称为权重。
• 偏置这个术语，有穿木屐的效果，即在没有任何输入时(输入为0时)，给输出穿上多高的木屐(加上多大的值)的意思。

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(x * w) + b
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

• 同理，也可以实现与非门和或门。

import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(x * w) + b
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

import numpy as np

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(x * w) + b
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

4. 感知机的局限性

4.1 异或门

• 首先指出，用前面介绍的感知机(式(2.1)和式(2.2))是无法实现异或门的逻辑功能的。那为什么这个感知机可以实现与门、或门、与非门，但无法实现异或门呢？
• 先解释为什么这个感知机可以实现或门：
  当权重参数为(b, w₁, w₂) = (-0.5, 1.0, 1.0)时，可实现或门的逻辑功能，此时感知机的表达式见式(2.3)。
  
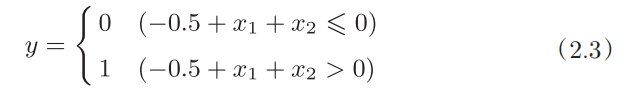
  式(2.3)表示的感知机会生成由直线 -0.5 + x₁ + x₂ = 0 分割开的两个空间。其中，一个空间输出1，另一个空间输出0。
  
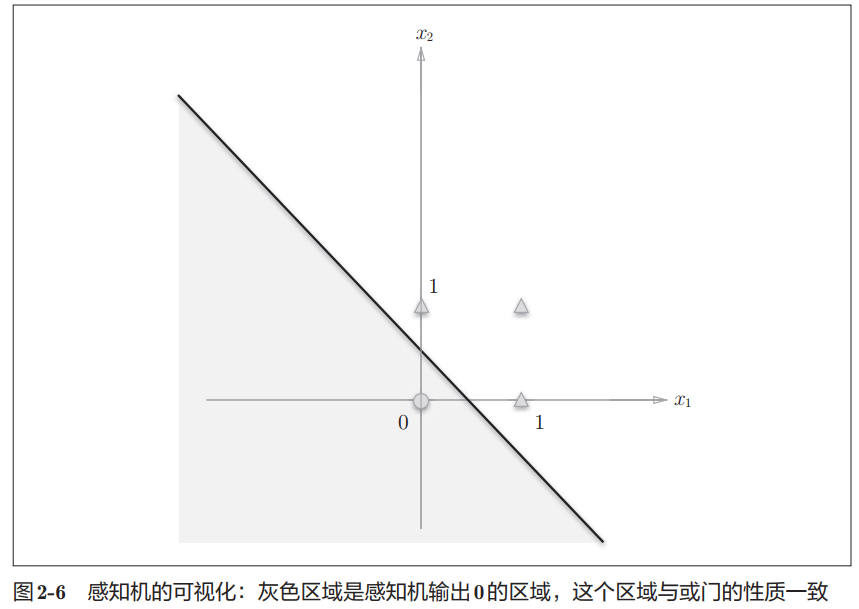
  如图所示，○表示输出为0，△表示输出为1，如果想要制作或门，就需要用一条直线把图中的○和△分开。正如上图中，直线 -0.5 + x₁ + x₂ = 0 就把○和△分开了，实现了或门的逻辑功能。
• 那么为什么这种感知机不能实现异或门呢：
  首先把异或门的输出利用图形化给表示出来。
  
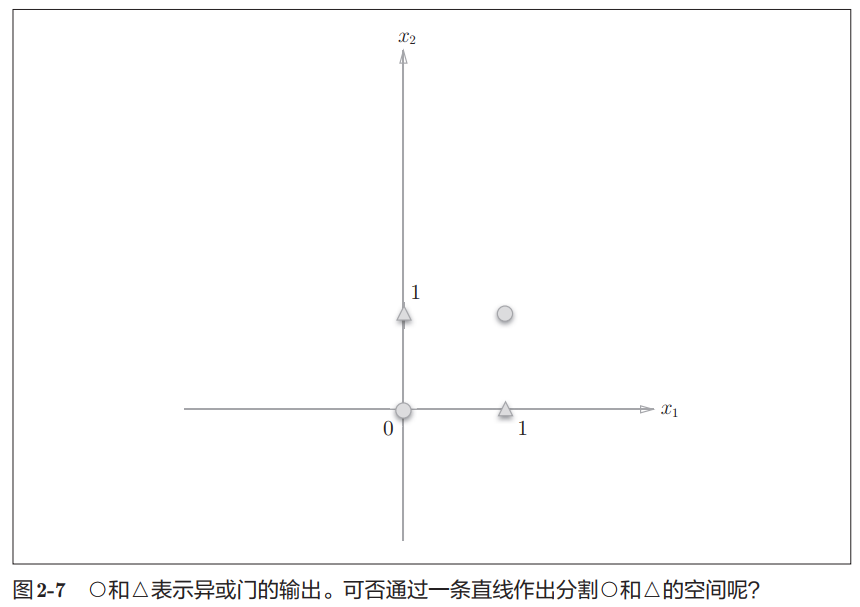
  我们发现，这样的输出空间是无法用一条直线将○和△分开的。也因此，用式(2.1)和式(2.2)表示的感知机是无法实现异或门的。

4.2 线性和非线性

• 虽然用直线无法将异或门的输出空间的○和△分开，但是如果利用曲线的话，就可以实现了。
  
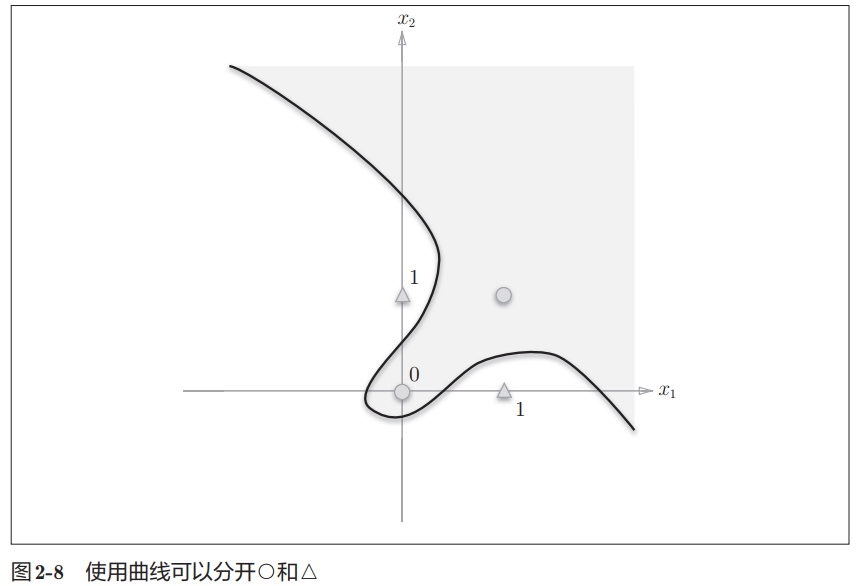
• 感知机的局限性就在于它只能表示由一条直线分割的空间。上图的弯曲的曲线是无法用感知机表示的。
• 上图中被曲线分割而成的空间称为非线性空间，相应的，由直线分割而成的空间称为线性空间。

5. 多层感知机

• 严格来讲，4节中所说的感知机的局限性指的是单层感知机的局限性，即单层感知机无法表示异或门或者单层感知机无法分离非线性空间。
• 单层感知机虽然不能表示异或门。但是，感知机可以叠加层，即可以通过组合感知机(叠加层)来表示异或门。

5.1 已有门电路的组合

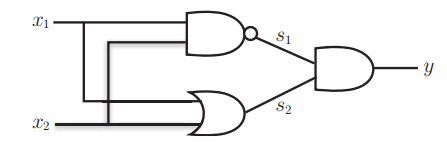
• 可以通过下图的门电路的组合来实现异或门的逻辑功能。
  

5.2 异或门的实现

• 首先，利用Python来实现异或门的逻辑功能，在编码过程中，我们参考了上图的组合门电路图和之前定义的AND函数、NAND函数、OR函数。

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(x * w) + b
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1
 
def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(x * w) + b
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1
    
def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(x * w) + b
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y
    
if __name__ == '__main__':
    print(XOR(0, 0))
    print(XOR(0, 1))
    print(XOR(1, 0))
    print(XOR(1, 1))

• 接下来使用叠加层的感知机来表示这个异或门。
  如下图所示，异或门是一种多层结构的神经网络，在下图中，将最左边的一列称为第0层，中间的一列称为第1层，最右边的一列称为第2层。
  下图的感知机的结构与实现与门、或门、与非门的感知机的结构不同。
  实现与门、或门、与非门的感知机是单层感知机，而实现异或门的是2层感知机。
  叠加了多层的感知机也称为多层感知机。
  
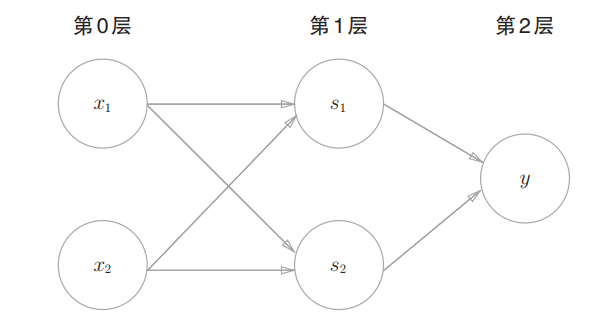
• 其传递流程为：
  1. 第0层的两个神经元接收输入信号，并将信号发送至第1层的神经元。
  2. 第1层的神经元将信号发送至第2层的神经元，第2层的神经元输出y。
• 上图中的感知机总共由3层构成，但因为拥有权重的层实质上只有两层(第0层和第1层之间，第1层和第2层之间)，所以称为“2层感知机”。（但是，部分文献认为上图的感知机是由3层构成的而将其称为“3层感知机”）

6. 从与非门到计算机

• 感知机通过叠加层能够进行非线性的表示，理论上还可以表示计算机进行处理。

7. 小结

• 感知机是具有输入和输出的算法。给定一个输入后，将输出一个既定的值。
• 感知机将权重和偏置设定为参数。
• 使用感知机可以表示与门和或门等逻辑电路。
• 异或门无法通过单层感知机来表示。
• 使用2层感知机可以表示异或门。
• 单层感知机只能表示线性空间，而多层感知机可以表示非线性空间。
• 多层感知机（在理论上）可以表示计算机。
• 感知机是学习神经网络的基础。

最后

以上就是震动心锁为你收集整理的深度学习入门基于Python的理论与实现_第二章_感知机(神经网络基础)前言1. 感知机是什么2. 简单逻辑电路3. 感知机的实现4. 感知机的局限性5. 多层感知机6. 从与非门到计算机7. 小结的全部内容，希望文章能够帮你解决深度学习入门基于Python的理论与实现_第二章_感知机(神经网络基础)前言1. 感知机是什么2. 简单逻辑电路3. 感知机的实现4. 感知机的局限性5. 多层感知机6. 从与非门到计算机7. 小结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。