神经网络入门案例保姆级教程

说明

本教程将结合经典的神经网络入门案例，通过绘图剖析网络中传播的细节，并附上详细的求导公式，希望能帮助读者更好地理解神经网络的工作过程，本教程需要你了解一些神经网络的基本知识。如果文中有错误，请各位大佬及时指正

案例

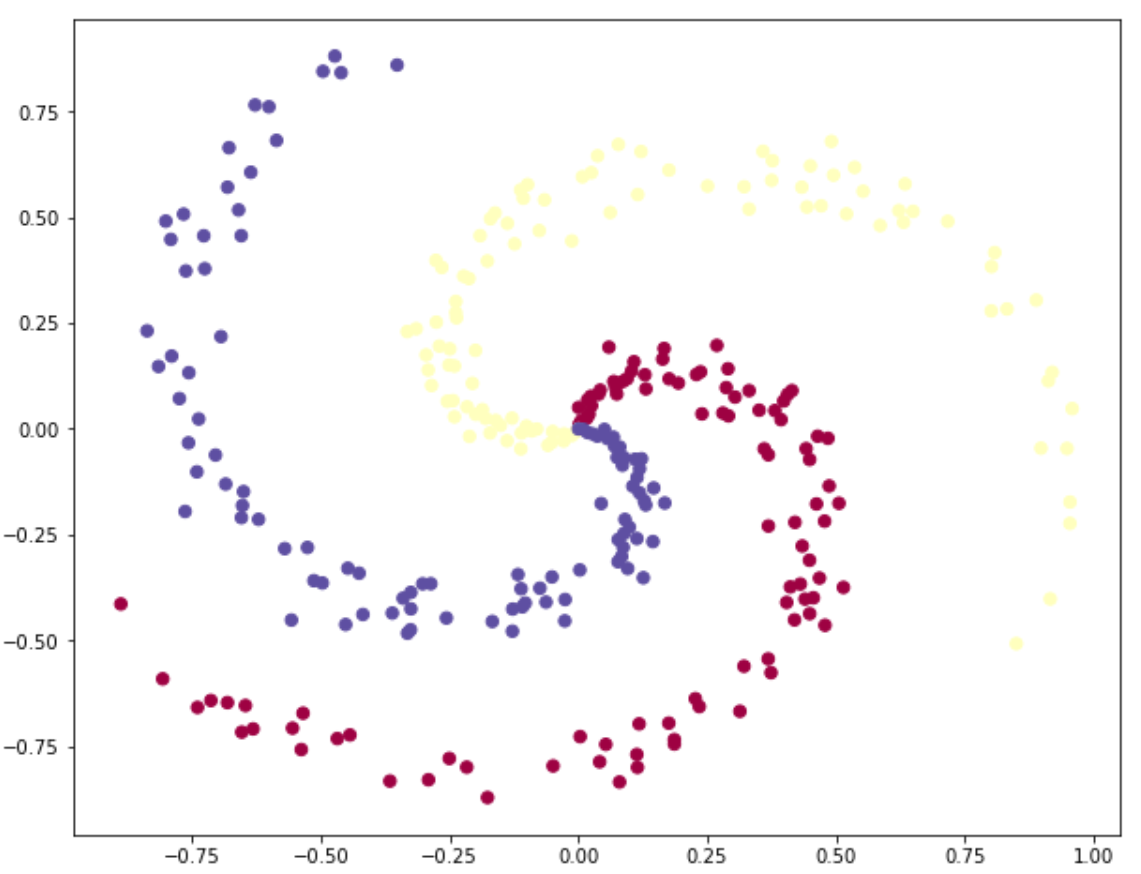
在本案例中，我们将随机生成三类样本点，要求使用分类器将这三类样本点进行分类。首先，我们将会使用普通的线性分类器（不带激活函数）来进行分类，再使用神经网络分类器（带激活函数）进行分类，最后对比两者的分类效果。在整个教程中，我会通过绘图来详细剖析分类器各层的含义和作用，再附上代码，阅读代码时，你可以对比着看分类器的结构图

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10.0, 8.0)

# 初始化参数
np.random.seed(0)
N = 100 # 每个类中的样本点
D = 2 # 维度
K = 3 # 类别个数
X = np.zeros((N*K, D)) # (300, 2)
y = np.zeros(N*K, dtype='uint8')
for j in range(K):
    ix = range(N*j, N*(j+1))
    r = np.linspace(0.0, 1, N) # 在0.0到1.0之间返回间隔均匀的N个数字
    t = np.linspace(j*4, (j+1)*4, N) + np.random.randn(N)*0.2
    X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] # 按行连接两个矩阵
    y[ix] = j
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)

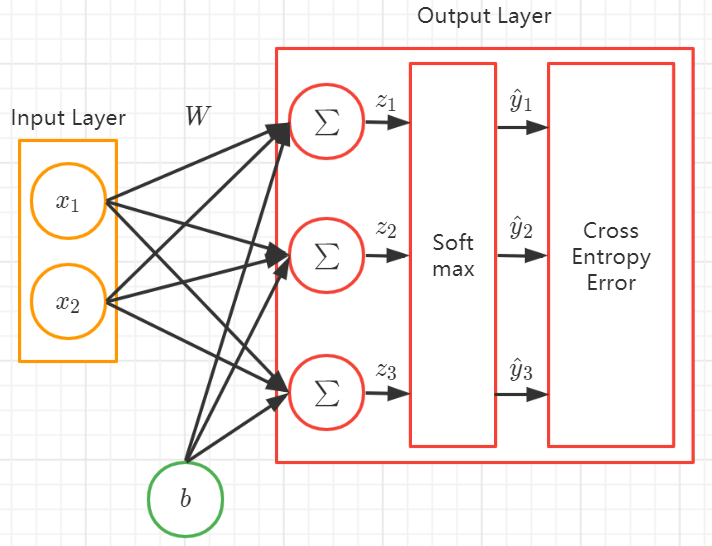
线性分类器

神经元

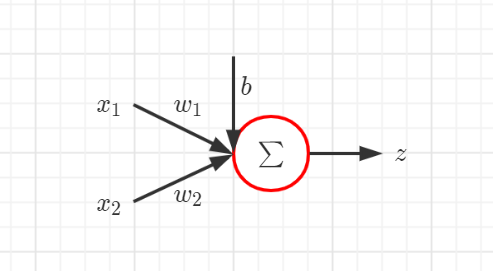
单个神经元的输出

$$z_i=\sum _i{x}_i{w}_i+b$$

其中 $x_i$ 表示样本的第 $i$ 个特征，$w_i$ 表示连接到该神经元的第 $i$ 个权重，$b$ 表示偏置，$z_i$ 表示该神经元的输出

以此类推，可得到整个网络的矩阵表示

$$Z\text{Z}Z=X\text{X}XW\text{W}W+b\text{b}b$$

梯度

$$\frac{\partial Z\text{Z}Z}{\partial W\text{W}W}=\frac{\partial (X\text{X}XW\text{W}W+b\text{b}b)}{\partial W\text{W}W}={X\text{X}X}^{\top }$$

$$\frac{\partial Z\text{Z}Z}{\partial b\text{b}b}=\frac{\partial (X\text{X}XW\text{W}W+b\text{b}b)}{\partial b\text{b}b}=I\text{I}I$$

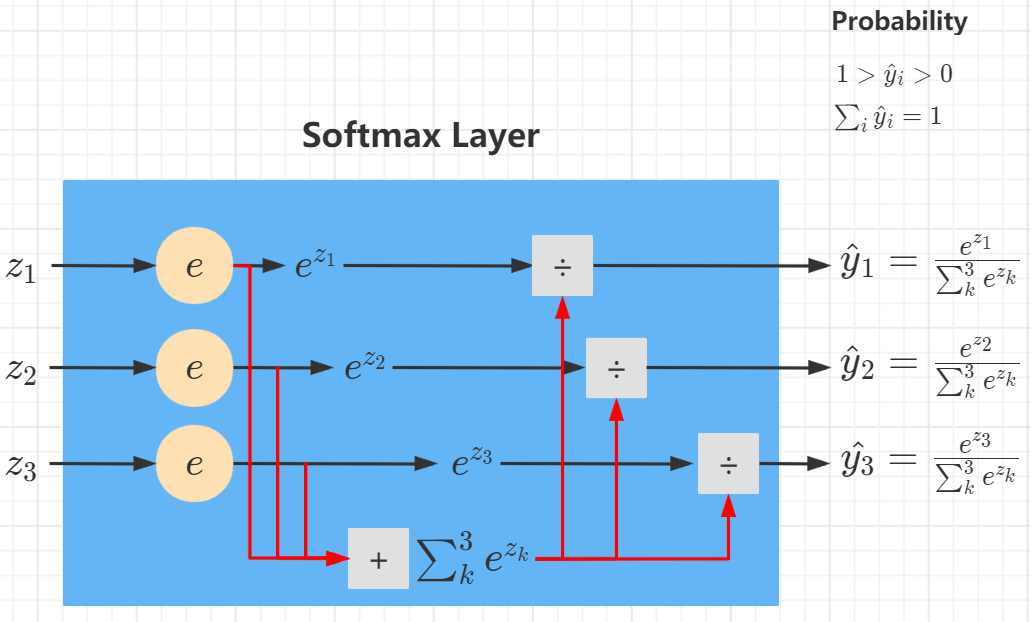
Softmax

$$S_i={\hat{y}}_i=\frac{e^{z_i}}{{\sum }_k{e}^{z_k}}$$

其中 $z_i$ 是第 $i$ 个输出单元的输出，${\hat{y}}_i$ 是 $z_i$ 经过 Softmax 转换后得到的概率值，表示样本属于第 $i$ 个类别的概率

梯度

若 $j=i$

$$\frac{\partial S_j}{\partial z_i}=\frac{\partial S_i}{\partial z_i}=\frac{\partial (\frac{e^{z_i}}{{\sum }_k{e}^{z_k}})}{\partial z_i}=\frac{{\sum }_k{e}^{z_k}{e}^{z_i}-(e^{z_i}{)}^2}{{\sum }_k(e^{z_k}{)}^2}=(\frac{e^{z_i}}{{\sum }_k{e}^{z_k}})(1-\frac{e^{z_i}}{{\sum }_k{e}^{z_k}})=S_i(1-S_i)$$

若 $j\ne i$

$$\frac{\partial S_j}{\partial z_i}=\frac{\partial (\frac{e^{z_j}}{{\sum }_k{e}^{z_k}})}{\partial z_i}=-e^{z_j}(\frac{1}{{\sum }_k{e}^{z_k}}{)}^2{e}^{z_i}=-S_i{S}_j$$

交叉熵损失

损失函数

$$L_i=-y_i\ln {\hat{y}}_i=-y_i\ln S_i$$

$$L=\sum _i{L}_i=-\sum _i{y}_i\ln S_i$$

其中 $i$ 表示第 $i$ 个类别，若样本的真实类别为 $i$，则 $y_i$ 为 1，否则为 0

梯度

$$\frac{\partial L_i}{\partial S_i}=\frac{\partial (-y_i\ln S_i)}{\partial S_i}=-y_i\frac{1}{S_i}$$

$$\begin{array}{rl}\frac{\partial L}{\partial z_i}=& \sum _j\frac{\partial L_j}{\partial S_j}\frac{\partial S_j}{\partial z_i}\\ =& \sum _{j=i}\frac{\partial L_j}{\partial S_j}\frac{\partial S_j}{\partial z_i}+\sum _{j\ne i}\frac{\partial L_j}{\partial S_j}\frac{\partial S_j}{\partial z_i}\\ =& -\frac{y_i}{S_i}{S}_i(1-S_i)+\sum _{j\ne i}\frac{y_j}{S_j}{S}_i{S}_j\\ =& -y_i+y_i{S}_i+\sum _{j\ne i}{y}_j{S}_i\\ =& -y_i+S_i\sum _j{y}_j\end{array}$$

针对分类问题，我们给定的结果 $y_i$ 最终只会有一个类别是 1，其他类别都是 0，因此，对于分类问题，梯度等于

$$\frac{\partial L}{\partial z_i}=S_i-y_i={\hat{y}}_i-y_i$$

正则化惩罚项

$$L_2=\frac{\lambda }{2}\sum _i\sum _j{w}_{ij}^2$$

梯度

$$\frac{\partial L_2}{\partial w_{ij}}=\lambda w_{ij}$$

矩阵形式

$$\frac{\partial L_2}{\partial W\text{W}W}=\lambda W\text{W}W$$

其中 $\lambda$ 为正则化系数

# 单层神经网络
# 初始化参数
W = 0.01 * np.random.randn(D, K) # 随机初始化参数 (2, 3)
b = np.zeros((1, K)) # (1, 3)
step_size = 1e-0 # 1.0，学习率
reg = 1e-3 # 0.001，正则化系数
num_examples = X.shape[0] # 样本个数
# 训练
for i in range(1000):
    
    # 前向传播
    scores = np.dot(X, W) + b # (300, 3)
    
    # softmax
    exp_scores = np.exp(scores)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # 计算类别概率 (300, 3)
    
    # 交叉熵损失
    corect_logprobs = -np.log(probs[range(num_examples), y])
    data_loss = np.sum(corect_logprobs) / num_examples # 对所有样本的损失进行求和，取均值
    
    # 正则化惩罚项
    reg_loss = 0.5 * reg * np.sum(W*W)
    
    loss = data_loss + reg_loss
    if i % 100 == 0:
        print('iteration %d: loss %f' % (i, loss))
    
    # 计算损失梯度 dL/dz
    dscores = probs
    dscores[range(num_examples), y] -= 1
    dscores /= num_examples # 将一批数据产生的梯度取平均
    
    # 计算在W，b上的梯度
    dW = np.dot(X.T, dscores) # (2, 3)
    db = np.sum(dscores, axis=0, keepdims=True) # (1, 3)
    
    # 加上正则项梯度
    dW += reg * W
    
    # 参数更新
    W += -step_size * dW
    b += -step_size * db

scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1) # 概率最大的类别的下标
print('training accuracy: %.2f' % (np.mean(predicted_class == y))) # 准确率

training accuracy: 0.49

h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b # ravel将多维数组降为一维
Z = np.argmax(Z, axis=1) # 取概率最高的类别
Z = Z.reshape(xx.shape)
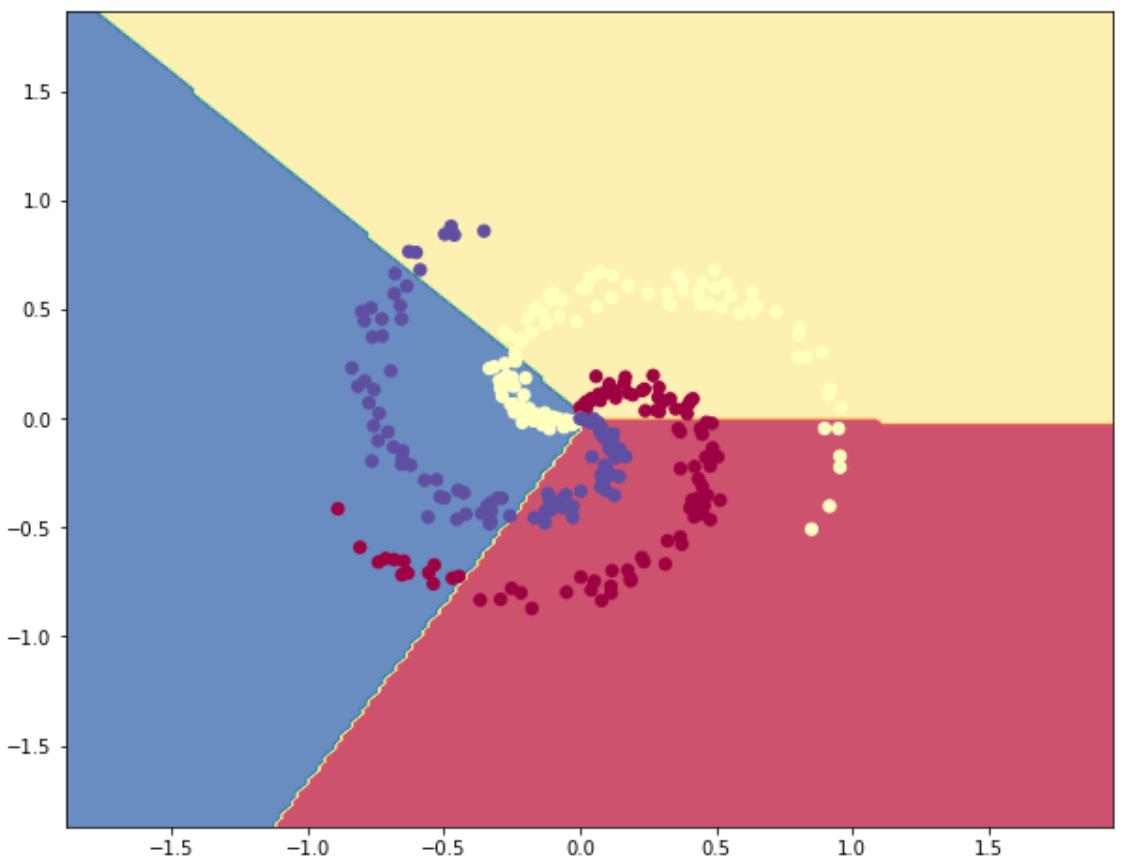
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8) # 绘制三维等高线
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

神经网络分类器

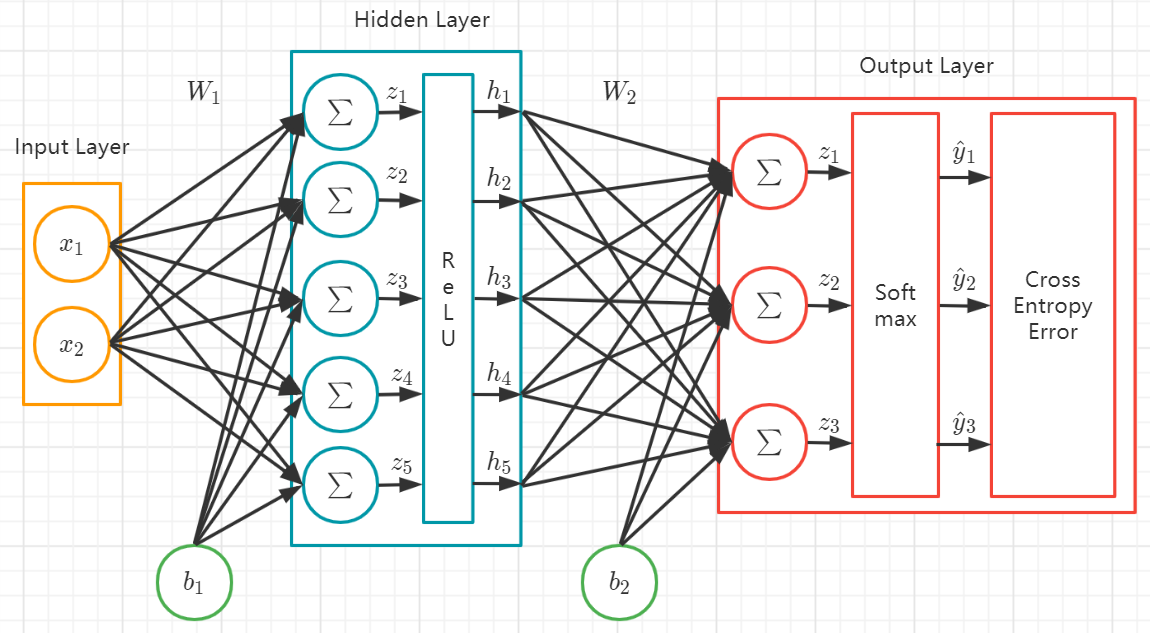
ReLU 激活单元

$$r=max(0,x)$$

梯度

$$\frac{dr}{dx}=\{\begin{array}{ll}0& x<=0\\ 1& x>0\end{array}$$

# 两层神经网络
# 初始化参数
h = 100 # 隐层大小（神经元个数）
W = 0.01 * np.random.randn(D, h)
b = np.zeros((1, h))
W2 = 0.01 * np.random.randn(h, K)
b2 = np.zeros((1, K))
step_size = 1e-0 # 学习率
reg = 1e-3 # 正则化系数
num_examples = X.shape[0] # 样本个数
# 训练
for i in range(10000):
    
    # 前向传播
    hidden_layer = np.maximum(0, np.dot(X, W) + b) # 使用 ReLU 激活函数
    scores = np.dot(hidden_layer, W2) + b2

    # softmax
    exp_scores = np.exp(scores)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # 计算类别概率

    # 交叉熵损失
    corect_logprobs = -np.log(probs[range(num_examples), y])
    data_loss = np.sum(corect_logprobs) / num_examples
    
    # 正则化惩罚项
    reg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2)
    
    loss = data_loss + reg_loss
    if i % 1000 == 0:
        print("iteration %d: loss %f" % (i, loss))

    # 计算损失梯度 dL/dz
    dscores = probs
    dscores[range(num_examples), y] -= 1
    dscores /= num_examples

    # 计算在W2，b2上的梯度
    dW2 = np.dot(hidden_layer.T, dscores)
    db2 = np.sum(dscores, axis=0, keepdims=True)
    dhidden = np.dot(dscores, W2.T)
    
    # ReLU 激活函数梯度
    dhidden[hidden_layer <= 0] = 0
    
    # 计算最后在W，b上的梯度
    dW = np.dot(X.T, dhidden)
    db = np.sum(dhidden, axis=0, keepdims=True)

    # 加上正则项梯度
    dW2 += reg * W2
    dW += reg * W

    # 参数更新
    W += -step_size * dW
    b += -step_size * db
    W2 += -step_size * dW2
    b2 += -step_size * db2

# 计算分类准确度
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print('training accuracy: %.2f' % (np.mean(predicted_class == y)))

training accuracy: 0.98

h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.maximum(0, np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b), W2) + b2
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

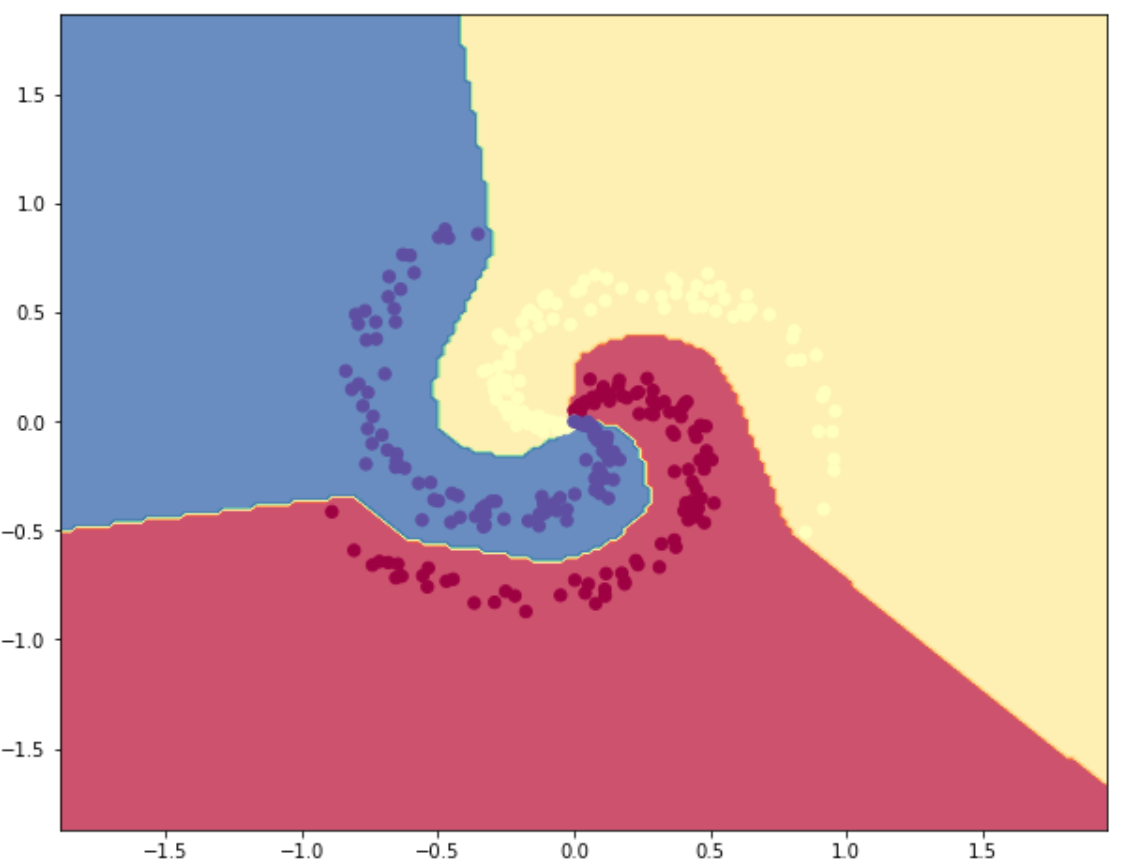
可以看到，神经网络由于引入了激活函数从而提升了分类器的非线性分类能力，由此我们可以感受到神经网络的强大魅力
完结，撒花！

最后

以上就是靓丽黄豆为你收集整理的神经网络入门案例保姆级教程的全部内容，希望文章能够帮你解决神经网络入门案例保姆级教程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。