机器学习sklearn-特征过程及数据预处理1 基本概念2 数据预处理 Preprocessing & Impute3 特征选择 

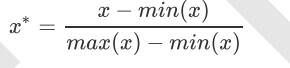
from sklearn.preprocessing import MinMaxScaler


data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]

#实现归一化
scaler=MinMaxScaler() #实例化
scaler=scaler.fit(data)   #训练
result=scaler.transform(data) #导出数据
print(result)
print(scaler.inverse_transform(result))#逆转 显示原来的数据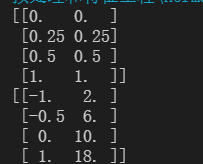

 调整归一化的范围

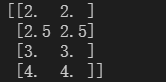
scaler=MinMaxScaler(feature_range=[2,4]) #实例化
scaler=scaler.fit(data)   #训练
result=scaler.transform(data) #导出数据
print(result)

使用numpy实现归一化

import numpy as np

#使用numpy实现归一化

X = np.array([[-1, 2], [-0.5, 6], [0, 10], [1, 18]])#将数据类型改为ndarray
#归一化 是针对列做的操作 指定axis=0
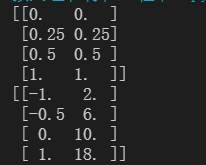
X_normal=(X-X.min(axis=0))/(X.max(axis=0)-X.min(axis=0))
print(X_normal)

#逆转归一化
X_returned = X_normal* (X.max(axis=0) - X.min(axis=0)) + X.min(axis=0)
print(X_returned)

2.1.2 数据标准化

  preprocessing.StandardScaler，当数据(x)按均值(μ)中心化后，再按标准差(σ)缩放，数据就会服从为均值为0，方差为1的正态分布（即标准正态分布），而这个过程，就叫做数据标准化(Standardization，又称Z-score normalization)，公式如下：

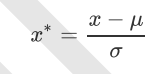
from sklearn.preprocessing import StandardScaler

data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
scaler=StandardScaler()
scaler.fit(data)
x_std=scaler.transform(data)
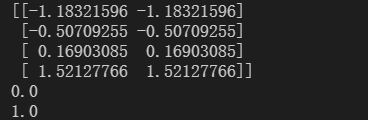
print(x_std)
print(x_std.mean())
print(x_std.std())

from numpy.core.arrayprint import printoptions
import pandas as pd
from sklearn.impute import SimpleImputer

data = pd.read_csv('Narrativedata.csv',index_col=0)#告知第0列是索引
# print(data.head())
# print(data.info())

#填补年龄
Age=data.loc[:,'Age'].values.reshape(-1,1)#-1,1将数据转换成一列 sklearn只接受二维以上
# print(Age.shape)

#实例化
imp_mean=SimpleImputer()
imp_median=SimpleImputer(strategy='median')
imp_0=SimpleImputer(strategy='constant',fill_value=0)

#训练并调出结果
imp_mean=imp_mean.fit_transform(Age)
imp_median=imp_median.fit_transform(Age)
imp_0=imp_0.fit_transform(Age)
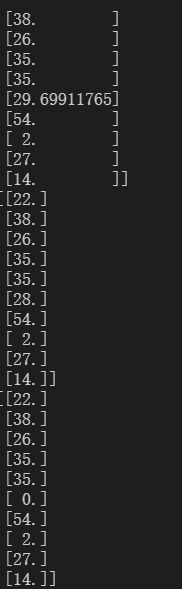
print(imp_mean[:10])
print(imp_median[:10])
print(imp_0[:10])

#使用众数填充embarked 众数可以包含文字型
Embarked = data.loc[:,"Embarked"].values.reshape(-1,1)
imp_most = SimpleImputer(strategy = "most_frequent")
data.loc[:,"Embarked"] = imp_most.fit_transform(Embarked)

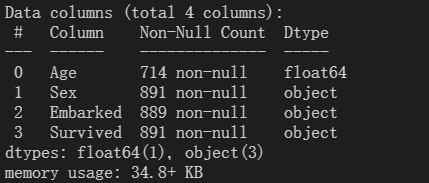
print(data.info())

也可以使用pandas的fillna和dropna对空值进行处理。

2.3 处理分类型数据：编码和哑变量

  在机器学习中，大多数算法，譬如逻辑回归，支持向量机SVM，k近邻算法等都只能够处理数值型数据，不能处理文字，在sklearn当中，除了专用来处理文字的算法，其他算法在fifit的时候全部要求输入数组或矩阵，也不能够导入文字型数据（其实手写决策树和普斯贝叶斯可以处理文字，但是sklearn中规定必须导入数值型）。

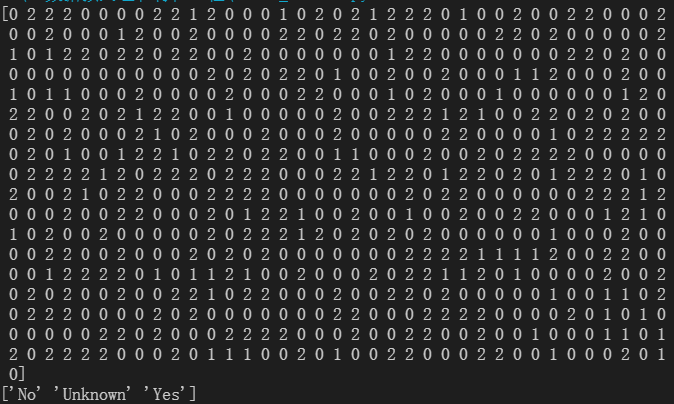
利用OrdinalEncoder将分类特征转换为分类数值。

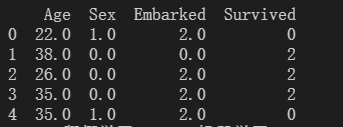
preprocessing.OneHotEncoder：独热编码，创建哑变量

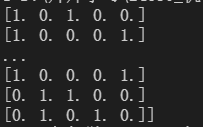
性别有两种类别，舱门有三种类别，所以转换出的哑变量有5列数据。

通过get_feature_names() 查看哑变量命名，并完成矩阵的合并。

from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OrdinalEncoder #特征专用，能够将分类特征转换为分类数值
from sklearn.preprocessing import OneHotEncoder #独热编码 创建哑变量
import numpy as np
import pandas as pd

data = pd.read_csv('Narrativedata.csv',index_col=0)#告知第0列是索引

#处理缺失值
data.loc[:,'Age']=data.loc[:,'Age'].fillna(data.loc[:,'Age'].mean())
data.dropna(axis=0,inplace=True)
data_=data.copy()
# print(data.info())

y=data.iloc[:,-1]  #取出标签 labelencoder输入的是标签而不是特征矩阵 所以不需要升维 1维即可
le=LabelEncoder()#实例化
le=le.fit(y)
label=le.transform(y) #调取结果
# print(label)
# print(le.classes_)#查看标签中类别
data.iloc[:,-1]=label #把标签数值化
#一步完成
# data.iloc[:,-1] = LabelEncoder().fit_transform(data.iloc[:,-1])

data_.iloc[:,1:-1] = OrdinalEncoder().fit_transform(data_.iloc[:,1:-1])
# print(data_.head(5))

#创建哑变量
X = data.iloc[:,1:-1] #取出要哑编码部分
enc = OneHotEncoder(categories='auto').fit(X)
result = enc.transform(X).toarray() #将结果转为数组
# print(result)

#依然可以还原
# print(pd.DataFrame(enc.inverse_transform(result)))

#连接矩阵生成新数据
newdata = pd.concat([data,pd.DataFrame(result)],axis=1) #左右拼接
# print(newdata.head())
#性别和舱门信息已经被哑变量替代 删除
newdata.drop(['Sex','Embarked'],axis=1,inplace=True) #删列
# print(newdata.head())
#更改列索引
#print(enc.get_feature_names()) #查看哑变量
newdata.columns=["Age","Survived","Female","Male","Embarked_C","Embarked_Q","Embarked_S"]
print(newdata.head())

2.4 处理连续性特征：二值化与分段

根据阈值将数据二值化（将特征值设置为 0 或 1 ），用于处理连续型变量。大于阈值的值映射为 1 ，而小于或等于阈值的值映射为0 。默认阈值为 0 时，特征中所有的正值都映射到 1 。二值化是对文本计数数据的常见操作，分析人员可以决定仅考虑某种现象的存在与否。它还可以用作考虑布尔随机变量的估计器的预处理步骤。

分段：preprocessing.KBinsDiscretizer

将连续型变量划分为分类变量的类，能够将连续型变量排序后按顺序分箱后编码。总共包含三个重要参数

3 特征选择 

3.1 过滤法

  过滤方法通常用作预处理步骤，特征选择完全独立于任何机器学习算法。它是根据各种统计检验中的分数以及相关性的各项指标来选择特征。

3.1.1 方差过滤

VarianceThreshold

通过特征本身的方差来筛选特征的类。比如一个特征本身的方差很小，就表示样本在这个特征上基本没有差异，可能特征中的大多数值都一样，甚至整个特征的取值都相同，那这个特征对于样本区分没有什么作用。所以无 论接下来的特征工程要做什么，都要优先消除方差为 0 的特征 。 VarianceThreshold 有重要参数 threshold ，表示方差的阈值，表示舍弃所有方差小于threshold 的特征，不填默认为 0 ，即删除所有的记录都相同的特征。

我们已经删除了方差为 0 的特征，但是依然剩下了 708 多个特征，明显还需要进一步的特征选择。然而，如果我们知道我们需要多少个特征，方差也可以帮助我们将特征选择一步到位。比如说，我们希望留下一半的特征，那可以设定一个让特征总数减半的方差阈值，只要找到特征方差的中位数，再将这个中位数作为参数threshold的值输入就好。

import numpy as np
import pandas as pd
from sklearn.feature_selection import VarianceThreshold

data = pd.read_csv('digit recognizor.csv')
# print(data.shape)
X = data.iloc[:,1:]  #数据
y = data.iloc[:,0] #标签

#消除方差为0的特征
selector=VarianceThreshold()
X_var0=selector.fit_transform(X)
# print(X_var0.shape)

#消除一半的特征 以方差中位数为threshold
X_halfvar=VarianceThreshold(np.median(X.var().values)).fit_transform(X)
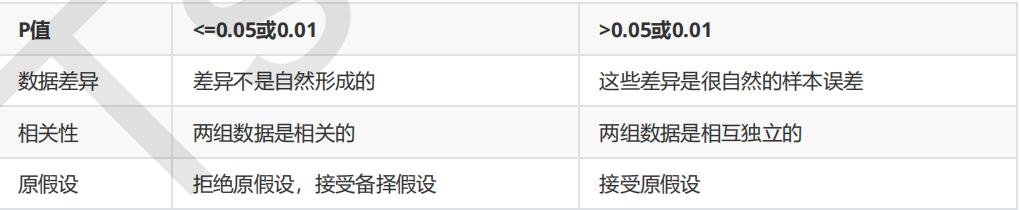
print(X_halfvar.shape)

 当特征是二分类时，特征的取值就是伯努利随机变量，这些变量的方差可以计算为：

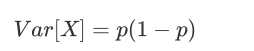
#若特征是伯努利随机变量，假设p=0.8，即二分类特征中某种分类占到80%以上的时候删除特征
X_bvar = VarianceThreshold(.8 * (1 - .8)).fit_transform(X)
X_bvar.shape

  方差过滤对模型效果的影响，以随机森林为例，进行方差过滤以后准确率和速度都有非常细微的提升。

  最近邻算法 KNN ，单棵决策树，支持向量机 SVM ，神经网络，回归算法，都需要遍历特征或升维来进行运算，所以他们本身的运算量就很大，需要的时间就很长，因此方差过滤这样的特征选择对他们来说就尤为重要。但对于不需要遍历特征的算法，比如随机森林，它随机选取特征进行分枝，本身运算就非常快速，因此特征选择对它来说效果平平。

  无论过滤法如何降低特征的数量，随机森林也只会选取固定数量的特征来建模；而最近邻算法就不同了，特征越少，距离计算的维度就越少，模型明显会随着特征的减少变得轻量。因

此，过滤法的 主要对象 是： 需要遍历特征或升维的算法们 ，而过滤法的 主要目的 是： 在维持算法表现的前提下，帮 助算法们降低计算成本。

  过滤法对随机森林无效，却对树模型有效。 从算法原理上来说，传统决策树需要遍历所有特征，计算不纯度后进行分枝，而随机森林却是随机选择特征进 行计算和分枝，因此随机森林的运算更快，过滤法对随机森林无用，对决策树却有用。

  

  之前我们使用的方差阈值是特征方差的中位数，因此属于阈值比较大，过滤掉的特征比较多的情

况。我们可以观察到，无论是 KNN 还是随机森林，在过滤掉一半特征之后，模型的精确度都上升了。这说明被我们过滤掉的特征在当前随机模式(random_state = 0) 下大部分是噪音。那我们就可以保留这个去掉了一半特征的数据，来为之后的特征选择做准备。当然，如果过滤之后模型的效果反而变差了，我们就可以认为，被我们过滤掉的特征中有很多都有有效特征，那我们就放弃过滤，使用其他手段来进行特征选择。

  

我们怎样知道，方差过滤掉的到底时噪音还是有效特征呢？过滤后模型到底会变好还是会变坏呢？ 答案是：每个数据集不一样，只能自己去尝试。这里的方差阈值，其实相当于是一个超参数，要选定最优的超参数，我们可以画学习曲线，找模型效果最好的点。但现实中，我们往往不会这样去做，因为这样会耗费大量的时间。我们只会使用阈值为0 或者阈值很小的方差过滤，来为我们优先消除一些明显用不到的特征，然后我们会选择更优的特征选择方法继续削减特征数量。

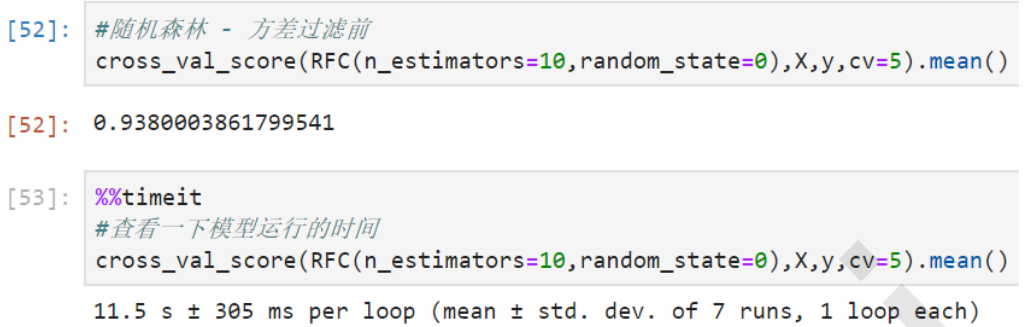
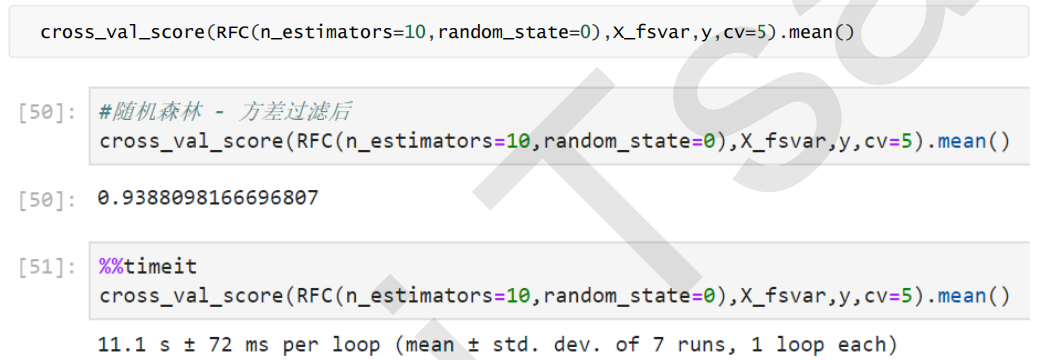
3.1.2 相关性过滤

我们希望选出与标签相关且有意义的特征，因为这样的特征能够为我们提供大量信息。如果特征与标签无关，那只会白白浪费我们的计算内存，可能还会给模型带来噪音。在sklearn 当中，我们有三种常用的方法来评判特征与标签之间的相关性：卡方， F 检验，互信息。

卡方过滤

卡方过滤是专门针对离散型标签（即分类问题）的相关性过滤。卡方检验类 feature_selection.chi2 计算每个非负特征和标签之间的卡方统计量，并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest这个可以输入” 评分标准 “ 来选出前 K个分数最高的特征的类，我们可以借此除去最可能独立于标签，与我们分类目的无关的特征。如果卡方检验检测到某个特征中所有的值都相同，会提示我们使用方差先进行方差过滤。

通过这条曲线，我们可以观察到，随着 K 值的不断增加，模型的表现不断上升，这说明， K 越大越好，数据中所有的特征都是与标签相关的。但是运行这条曲线的时间同样也是非常地长，接下来我们就来介绍一种更好的选择k 的方法：看p 值选择 k 。

卡方检验的本质是推测两组数据之间的差异，其检验的原假设是” 两组数据是相互独立的 ” 。卡方检验返回卡方值和P值两个统计量，其中卡方值很难界定有效的范围，而 p 值，我们一般使用 0.01 或 0.05 作为显著性水平，即 p 值判断的边界，具体我们可以这样来看：

F检验

又称 ANOVA ，方差齐性检验，是用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类，因此包含feature_selection.f_classif （

F 检验分类）和 feature_selection.f_regression （F检验回 归）两个类。其中F 检验分类用于标签是离散型变量的数据，而 F 检验回归用于标签是连续型变量的数据。 和卡方检验一样，这两个类需要和类SelectKBest 连用，并且我们也可以直接通过输出的统计量来判断我们到底要设置一个什么样的K 。需要注意的是， F 检验在数据服从正态分布时效果会非常稳定，因此如果使用 F 检验过滤，我们会先将数据转换成服从正态分布的方式。

F 检验的本质是寻找两组数据之间的线性关系，其原假设是 ” 数据不存在显著的线性关系 “ 。它返回 F 值和 p 值两个统计量。和卡方过滤一样，我们希望选取 p 值小于 0.05 或 0.01 的特征，这些特征与标签时显著线性相关的 ，而 p 值大于0.05或 0.01 的特征则被我们认为是和标签没有显著线性关系的特征，应该被删除。

 

from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest#找出分数最高k个的特征的类
from sklearn.feature_selection import chi2#卡方检验
from sklearn.feature_selection import f_classif #f检验
import numpy as np
import pandas as pd
from sklearn.feature_selection import VarianceThreshold
import matplotlib.pyplot as plt

data = pd.read_csv('digit recognizor.csv')
X = data.iloc[:,1:]  #数据
y = data.iloc[:,0] #标签
X_halfvar=VarianceThreshold(np.median(X.var().values)).fit_transform(X)
#假设在这里我一直我需要300个特征
# X_fschi = SelectKBest(chi2, k=350).fit_transform(X_halfvar, y) #评估统计量使用卡方 选前300个
# print(X_fschi.shape)

#绘制学习曲线查看模型效果
# score=[]
# for i in range(390,120,-10):
#     X_fschi = SelectKBest(chi2, k=i).fit_transform(X_halfvar, y)
#     once=cross_val_score(RFC(n_estimators=10),X_halfvar,y,cv=10).mean()
#     score.append(once)

# plt.plot(range(390,120,-10),score)
# plt.show()

#f检验
F,pvalues_f = f_classif(X_halfvar,y)#获取f检验两个参数
k=F.shape[0]-(pvalues_f>0.05).sum() #求出合适的k值
print(k)
X_fsF = SelectKBest(f_classif, k=392).fit_transform(X_halfvar, y)
score=cross_val_score(RFC(n_estimators=10),X_fsF,y,cv=5).mean()
print(score)

互信息法

互信息法是用来捕捉每个特征与标签之间的任意关系（包括线性和非线性关系）的过滤方法。和 F 检验相似，它既可以做回归也可以做分类，并且包含两个类feature_selection.mutual_info_classif （互信息分类）和 feature_selection.mutual_info_regression （互信息回归）。这两个类的用法和参数都和 F 检验一模一样，不过互信息法比F 检验更加强大， F 检验只能够找出线性关系，而互信息法可以找出任意关系。

互信息法不返回 p 值或 F 值类似的统计量，它返回 “ 每个特征与目标之间的互信息量的估计 ” ，这个估计量在 [0,1] 之间取值，为0 则表示两个变量独立，为 1 则表示两个变量完全相关。

所有特征的互信息量估计都大于 0 ，因此所有特征都与标签相关。

#互信息法
result=mutual_info_classif(X_halfvar,y)
k=result.shape[0]-sum(result<=0)
print(k)

3.2 嵌入法

嵌入法是一种让算法自己决定使用哪些特征的方法，即特征选择和算法训练同时进行。在使用嵌入法时，我们先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据权值系数从大到小选择特征。这些权值系数往往代表了特征对于模型的某种贡献或某种重要性，比如决策树和树的集成模型中的feature_importances_ 属性，可以列出各个特征对树的建立的贡献，我们就可以基于这种贡献的评估，找出对模型建立最有用的特征。因此相比于过滤法，嵌入法的结果会更加精确到模型的效用本身，对于提高模型效力有更好的效果。并且，由于考虑特征对模型的贡献，因此无关的特征（需要相关性过滤的特征）和无区分度的特征（需要方差过滤的特征）都会因为

缺乏对模型的贡献而被删除掉，可谓是过滤法的进化版。

过滤法中使用的统计量可以使用统计知识和常识来查找范围（如 p 值应当低于显著性水平 0.05 ），而嵌入法中使用的权值系数却没有这样的范围可找—— 我们可以说，权值系数为 0 的特征对模型丝毫没有作用，但当大量特征都对模型有贡献且贡献不一时，我们就很难去界定一个有效的临界值。这种情况下，模型权值系数就是我们的超参数，我们或许需要学习曲线，或者根据模型本身的某些性质去判断这个超参数的最佳值究竟应该是多少。

feature_selection.SelectFromModel

SelectFromModel 是一个元变换器，可以与任何在拟合后具有 coef_ ， feature_importances_ 属性或参数中可选惩罚项的评估器一起使用（比如随机森林和树模型就具有属性feature_importances_ ，逻辑回归就带有 l1 和 l2 惩罚项，线性支持向量机也支持l2 惩罚项）。

对于有 feature_importances_ 的模型来说，若重要性低于提供的阈值参数，则认为这些特征不重要并被移除。feature_importances_的取值范围是 [0,1] ，如果设置阈值很小，比如 0.001 ，就可以删除那些对标签预测完全没贡献的特征。如果设置得很接近1 ，可能只有一两个特征能够被留下。

 

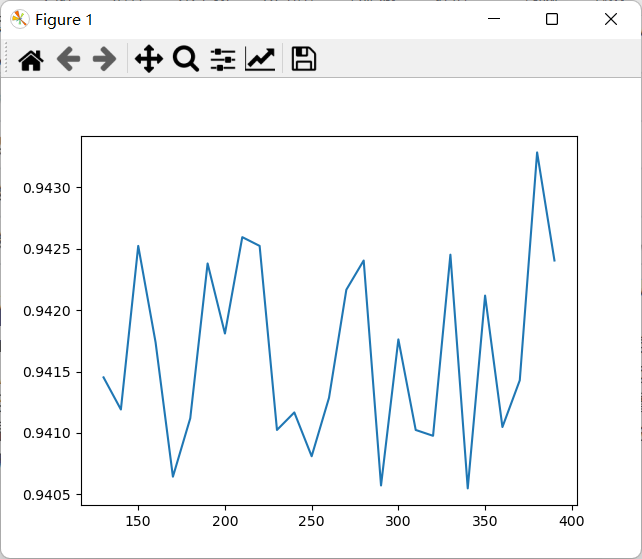
 使用随机森林为例，则需要学习曲线来帮助我们寻找最佳特征值。

从图像上来看，随着阈值越来越高，模型的效果逐渐变差，被删除的特征越来越多，信息损失也逐渐变大。但是在0.002之前，模型的效果都可以维持在 0.93 以上。

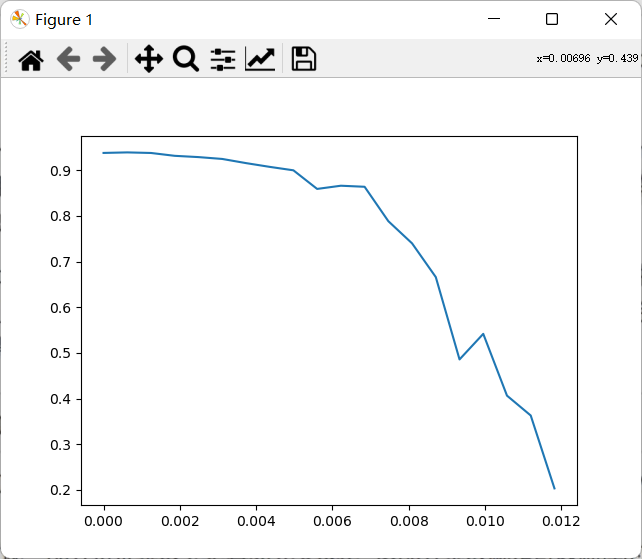
from sklearn.feature_selection import  SelectFromModel
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
import pandas as pd
import numpy as np
import  matplotlib.pyplot as plt

#读取数据
data = pd.read_csv('digit recognizor.csv')
X = data.iloc[:,1:]  #数据
y = data.iloc[:,0] #标签


RFC_=RFC(n_estimators=10)#随机森林实例化
feature_im=RFC_.fit(X,y).feature_importances_
# print(feature_im)
threshold=np.linspace(0,feature_im.max(),20)#从0开始生成20个threshold
# print(threshold)

#绘制学习曲线
score=[]
for i in threshold:
    x_embeded=SelectFromModel(RFC_,threshold=i).fit_transform(X,y)#实例化嵌入法
    once=cross_val_score(RFC_,x_embeded,y,cv=5).mean()
    score.append(once)

plt.plot(threshold,score)
plt.show()

3.3 包装法

包装法也是一个特征选择和算法训练同时进行的方法，与嵌入法十分相似，它也是依赖于算法自身的选择，比如coef_属性或 feature_importances_ 属性来完成特征选择。但不同的是，我们往往使一个目标函数作为黑盒来帮助我们选取特征，而不是自己输入某个评估指标或统计量的阈值。包装法在初始特征集上训练评估器，并且通过coef_属性或通过 feature_importances_ 属性获得每个特征的重要性。然后，从当前的一组特征中修剪最不重要的特征。在修剪的集合上递归地重复该过程，直到最终到达所需数量的要选择的特征。区别于过滤法和嵌入法的一次训练解决所有问题，包装法要使用特征子集进行多次训练，因此它所需要的计算成本是最高的。

包装法的效果是所有特征选择方法中最利于提升模型表现的，它可以使用很少的特征达到很优秀的效果。除此之外，在特征数目相同时，包装法和嵌入法的效果能够匹敌，不过它比嵌入法算得更见缓慢，所以也不适用于太大型的数据。相比之下，包装法是最能保证模型效果的特征选择方法。

feature_selection.RFE

参数 estimator 是需要填写的实例化后的评估器， n_features_to_select 是想要选择的特征个数， step 表示每次迭代中希望移除的特征个数。除此之外，RFE 类有两个很重要的属性， .support_ ：返回所有的特征的是否最后被选中的布尔矩阵，以及.ranking_ 返回特征的按数次迭代中综合重要性的排名。

3.4 特征选择总结

每种方法的原理都不同，并且都涉及到不同调整方法的超参数。经验来说，过滤法更快速，但更粗糙。包装法和嵌入法更精确，比较适合具体到算法去调整，但计算量比较大，运行时间长。当数据量很大的时候，优先使用方差过滤和互信息法调整，再上其他特征选择方法。使用逻辑回归时，优先使用嵌入法。使用支持向量机时，优先使用包装法。迷茫的时候，从过滤法走起，看具体数据具体分析。