机器学习入门 03 线性回归法（Linear Regression）

1 简单线性回归

1.1 介绍

1）特点：

• 样本特征只有一个
• 解决回归问题
• 思想简单，实现容易
• 许多强大的非线性模型的基础
• 结果有很好的解释性

1.2 思想、公式

1.2.1 思想

寻找出一条直线，最大程度的“拟合”样本特征和样本输出标记之间的关系。

通过分析问题，确定问题的损失函数（loss function）或效用函数（utility function）；

通过最优化损失函数（min）或效用函数（max），获得机器学习的模型。

近乎所有参数学习算法都是这样的套路。

1.2.2 公式

线性关系：$y=ax+b$

对应关系：$y^{(i)}=a{x}^{(i)}+b$, ${\stackrel{\wedge }{y}}^{(i)}=a{x}^{(i)}+b$

• $x^{(i)}$为样本点的值
• $y^{(i)}$为样本对应的真实值
• ${\stackrel{\wedge }{y}}^{(i)}$为预测值

表达差距（损失函数）：${\left(y^{(i)}-{\stackrel{\wedge }{y}}^{(i)}\right)}^2$

考虑所有的样本的差距：${\sum }_{i=1}^m{\left(y^{(i)}-{\stackrel{\wedge }{y}}^{(i)}\right)}^2={\sum }_{i=1}^m{\left(y^{(i)}-a{x}^{(i)}-b\right)}^2$

简单线性回归的目标：找到 a，b 使得上式的值最小。

1.2.3 求出 a，b

目标函数：$f={\sum }_{i=1}^m{\left(y^{(i)}-a{x}^{(i)}-b\right)}^2$

1）分别对 a，b 求一阶导，令其导函数为0，求解 a，b

$$\begin{gathered} \frac{\sigma f}{\sigma b}=0 \\ {\sum }_{i=1}^{m}2\left(y^{(i)}-a{x}^{(i)}-b\right)\left(-1\right)=0 \\ {\sum }_{i=1}^m\left(y^{(i)}-a{x}^{(i)}-b\right)=0 \\ {\sum }_{i=1}^m{y}^{(i)}-{\sum }_{i=1}^{m}a{x}^{(i)}-{\sum }_{i=1}^{m}b=0 \\ {\sum }_{i=1}^m{y}^{(i)}-{\sum }_{i=1}^{m}a{x}^{(i)}-mb=0 \\ mb={\sum }_{i=1}^m{y}^{(i)}-{\sum }_{i=1}^{m}a{x}^{(i)} \\ b=\overline{y}-a\overline{x} \end{gathered}$$

$$\begin{gathered} \frac{\sigma f}{\sigma a}=0 \\ {\sum }_{i=1}^{m}2\left(y^{(i)}-a{x}^{(i)}-b\right)\left(-x^{(i)}\right)=0 \\ {\sum }_{i=1}^m\left(y^{(i)}-a{x}^{(i)}-b\right)(x^{(i)})=0 \\ {\sum }_{i=1}^m\left(y^{(i)}-a{x}^{(i)}-\overline{y}+a\overline{x}\right)(x^{(i)})=0 \\ {\sum }_{i=1}^m\left({x^{(i)}y}^{(i)}-a{(x}^{(i)}{)}^2-x^{(i)}\overline{y}+a\overline{x}{x}^{(i)}\right)=0 \\ {\sum }_{i=1}^m({x^{(i)}y}^{(i)}-x^{(i)}\overline{y})-{\sum }_{i=1}^m(a{(x}^{(i)}{)}^2-a\overline{x}{x}^{(i)})=0 \\ {\sum }_{i=1}^m({x^{(i)}y}^{(i)}-x^{(i)}\overline{y})-a{\sum }_{i=1}^m({(x}^{(i)}{)}^2-\overline{x}{x}^{(i)})=0 \\ a=\frac{{\sum }_{i=1}^m({x^{(i)}y}^{(i)}-x^{(i)}\overline{y})}{{\sum }_{i=1}^m({(x}^{(i)}{)}^2-\overline{x}{x}^{(i)})} \\ \because \sum x^{(i)}\overline{y}=\overline{y}\sum x^{(i)}=m\overline{x}\overline{y}=\sum \overline{x}\overline{y}=\overline{x}\sum y^{(i)}=\sum \overline{x}{y}^{(i)} \\ \therefore a=\frac{{\sum }_{i=1}^m({x^{(i)}y}^{(i)}-x^{(i)}\overline{y}-\overline{x}{y}^{(i)}+\overline{x}\overline{y})}{{\sum }_{i=1}^m({(x}^{(i)}{)}^2-\overline{x}{x}^{(i)}-\overline{x}{x}^{(i)}+{(\overline{x})}^2)}=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m{(x^{(i)}-\overline{x})}^2} \end{gathered}$$

2）a与b的值

$a=\frac{{\sum }_{i=1}^m({x^{(i)}y}^{(i)}-x^{(i)}\overline{y}-\overline{x}{y}^{(i)}+\overline{x}\overline{y})}{{\sum }_{i=1}^m({(x}^{(i)}{)}^2-\overline{x}{x}^{(i)}-\overline{x}{x}^{(i)}+{(\overline{x})}^2)}=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m{(x^{(i)}-\overline{x})}^2}$

$b=\overline{y}-a\overline{x}$

2 衡量线性回归算法的指标

2.1 均方误差 MSE（Mean Squared Error）

$$f=\frac{1}{m}\sum {(y_{test}^{(i)}-{\hat{y}}_{test}^{(i)})}^2$$

2.2 均方根误差 RMSE（Root Mean Squared Error）

$$f=\sqrt{{MSE}_{test}}=\sqrt{\frac{1}{m}\sum {(y_{test}^{(i)}-{\hat{y}}_{test}^{(i)})}^2}$$

2.3 平均绝对误差 MAE（Mean Absolute Error）

$$f=\frac{1}{m}\sum \left|y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}\right|$$

2.4 R Squared

$$\begin{gathered} R^2=1-\frac{{SS}_{residual}}{{SS}_{total}}=1-\frac{{\sum }_{i=1}^m{({\hat{y}}^{(i)}-y^{(i)})}^2}{{\sum }_{i=1}^m{(\overline{y}-y^{(i)})}^2} \\ =1-\frac{{\sum }_{i=1}^m{({\hat{y}}^{(i)}-y^{(i)})}^2/m}{{\sum }_{i=1}^m{(\overline{y}-y^{(i)})}^2/m}=1-\frac{MSE(\hat{y},y)}{var(y)} \end{gathered}$$

• ${SS}_{residual}$ --> Residual sum of squares
• ${SS}_{total}$ --> Total sum of squares
• $var(y)$ --> y的方差

性质：

• $R^2$越大越好，当预测模型不犯错误时，$R^2$=1
• $R^2$<=1
• 当预测模型=基准模型时，$R^2$=0
• 如果$R^2$<0，则我们的模型还不如基准模型，即意味着我们的数据不存在任何的线性关系。

3 多元线性回归和正规方程解

1）多元线性回归的样本特征有多个。
2）表达式：

• $y={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n，x_0\equiv 1$
• ${\hat{y}}^{(i)}={\theta }_0{x}_0^{(i)}+{\theta }_1{x}_1^{(i)}+{\theta }_2{x}_2^{(i)}+\dots {\theta }_n{x}_n^{(i)}，x_0^{(i)}\equiv 1$

3）差距表达式：$f={\sum }_{i=1}^m{(y^{(i)}-{\hat{y}}^{(i)})}^2={(\overrightarrow{y}-\overrightarrow{x_b})}^{⊺}(\overrightarrow{y}-\overrightarrow{x_b})$

4）目标：找到$\overrightarrow{\theta }={({\theta }_0,{\theta }_1,{\theta }_2,\dots ,{\theta }_n,)}^{⊺}$，使得上式 $f$ 的值最小。

• $\overrightarrow{x_b}=\left\{\begin{array}{ccccc}1& x_1^{(1)}& x_2^{(1)}& \dots & x_n^{(1)}\\ 1& x_1^{(2)}& x_2^{(2)}& \dots & x_n^{(2)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_1^{(m)}& x_2^{(m)}& \dots & x_n^{(m)}\end{array}\right\}$
• $\overrightarrow{\hat{y}}=\overrightarrow{x_b}\vec{\theta }$
• ${\theta }_0$ 为截距（intercept),${\theta }_0\cdots {\theta }_n$ 为系数（coefficients)。

5）求解，对 $f$ 求导可求出$\vec{\theta }$，即多元线性回归的正规方程解（Normal Equation）

$\vec{\theta }={(x_b^{⊺}{x}_b)}^{-1}{x}_b^{⊺}y$

此公式特点：

• 问题：时间复杂度高，O(n ^ 3)，优化后O(n^2.4)。
• 优点：不需要进行数据归一化处理。

4 代码

4.1 简单线性回归

1）SimpleLR.py

import numpy as np
from comm_utils.testCapability import r2_score


class SimpleLinearRegression:

    def __init__(self):
        """ 初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """ 根据训练数据集x_train,y_train训练simple LR 模型"""
        assert x_train.ndim == 1, "simple LR can only solve single feature traing data."
        assert len(x_train) == len(y_train), "the size of x_train must be equal to the size of y_train"

        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        # 使用向量的方式计算
        self.a_ = (x_train - x_mean).dot(y_train - y_mean) / (x_train - x_mean).dot(x_train - x_mean)
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """ 给定待预测数据集x_predict,返回表示x_predict的结果向量"""
        assert x_predict.ndim == 1, "simple LR can only solve single feature traing data."
        assert self.a_ is not None and self.b_ is not None, "must fit before predict."

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """ 给定单个待预测数据x，返回x的预测结果值"""
        return self.a_ * x_single + self.b_

    def score(self, x_test, y_test):
        """ 根据测试数据集 x_test 和 y_test 确定当前模型的准确度"""
        y_predict = self.predict(x_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "simpleLR()"

4.2 多元线性回归

1）LinearRegression.py

import numpy as np
from comm_utils.testCapability import r2_score


class LinearRegression:

    def __init__(self):
        """ 初识化 LR 模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def fit_normal(self, x_train, y_train):
        """ 根据训练数据集x_train,y_train训练LR模型"""
        assert x_train.shape[0] == y_train.shape[0], "the size of x_train must be equal to the size of y_train"

        # 在第一列前添加一列1
        x_b = np.hstack([np.ones((len(x_train), 1)), x_train])
        self._theta = np.linalg.inv(x_b.T.dot(x_b)).dot(x_b.T).dot(y_train)

        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, x_predict):
        """ 给定待预测数据集x_predict,返回表示x_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, "must fit before predict."
        assert x_predict.shape[1] == len(self.coef_), "the feature number of x_predict must be equal to x_train"

        x_b = np.hstack([np.ones((len(x_predict), 1)), x_predict])
        return x_b.dot(self._theta)

    def score(self, x_test, y_test):
        """ 根据测试数据集 x_test 和 y_test 确定当前模型的准确度"""
        y_predict = self.predict(x_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

4.3 测试

1）model_selection.py

import numpy as np


def train_test_split(x, y, test_reaio=0.2, seed=None):
    """ 将数据x和y按照test_ratio分割成x_train,x_test,y_train,y_test"""

    assert x.shape[0] == y.shape[0], "the size of x must be equal to the y"
    assert 0.0 <= test_reaio <= 1.0, "test_ratio must be valid"

    if seed:
        np.random.seed(seed)

    shuffled_indexes = np.random.permutation(len(x))

    test_size = int(len(x) * test_reaio)
    test_indexes = shuffled_indexes[:test_size]
    train_indexes = shuffled_indexes[test_size:]

    x_train = x[train_indexes]
    y_train = y[train_indexes]

    x_test = x[test_indexes]
    y_test = y[test_indexes]

    return x_train, x_test, y_train, y_test

2）testCapability.py

import numpy as np
from math import sqrt


def accuracy_score(y_true, y_predict):
    """ 计算y_true和y_predict之间的准确率"""
    assert len(y_true) == len(y_predict), 
        "the size of y_true must be equal to the size of y_predict"

    return np.sum(y_true == y_predict) / len(y_true)


def mean_squared_error(y_true, y_predict):
    """ 计算y_true和y_predict之间的MSE"""
    assert len(y_true) == len(y_predict), 
        "the size of y_true must be equal to the size of y_predict"

    return np.sum((y_true - y_predict) ** 2) / len(y_true)


def root_mean_squared_error(y_true, y_predict):
    """ 计算y_true和y_predict之间的RMSE"""

    return sqrt(mean_squared_error(y_true, y_predict))


def mean_absolute_error(y_true, y_predict):
    """ 计算y_true和y_predict之间的MAE"""
    assert len(y_true) == len(y_predict), 
        "the size of y_true must be equal to the size of y_predict"

    return np.sum(np.absolute(y_true - y_predict)) / len(y_true)


def r2_score(y_true, y_predict):
    """ 计算y_true和y_predict之间的R Square"""

    return 1 - mean_squared_error(y_true, y_predict) / np.var(y_true)

3）test.py

import matplotlib.pyplot as plt
from sklearn import datasets
from comm_utils.model_selection import train_test_split
import LinearRegression_pro.SimpleLR

# 准备数据，波士顿房产数据
boston = datasets.load_boston()
print(boston.feature_names)
x = boston.data[:, 5]  # 只使用房间数量这个特征
print(x.shape)
y = boston.target
print(y.shape)
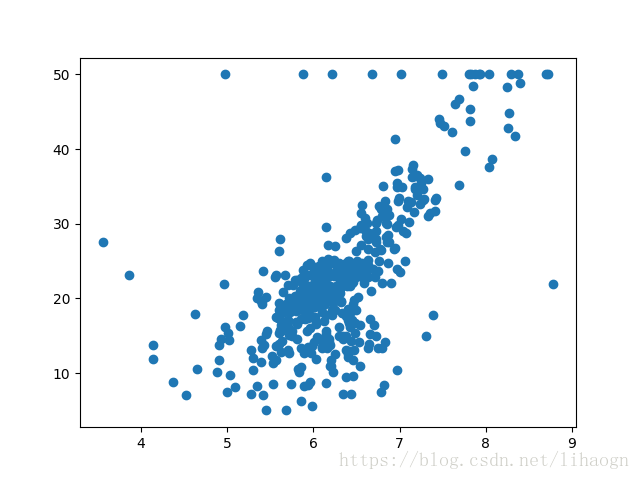
# 绘制图
plt.scatter(x, y)
plt.show()

# 去除 y 为50的特殊值
x = x[y < 50.0]
y = y[y < 50.0]

plt.scatter(x, y)


# 使用简单线性回归法

# 1 拆分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y)
# 2 拟合
slr = LinearRegression_pro.SimpleLR.SimpleLinearRegression()
slr.fit(x_train, y_train)
print(slr.score(x_test, y_test))
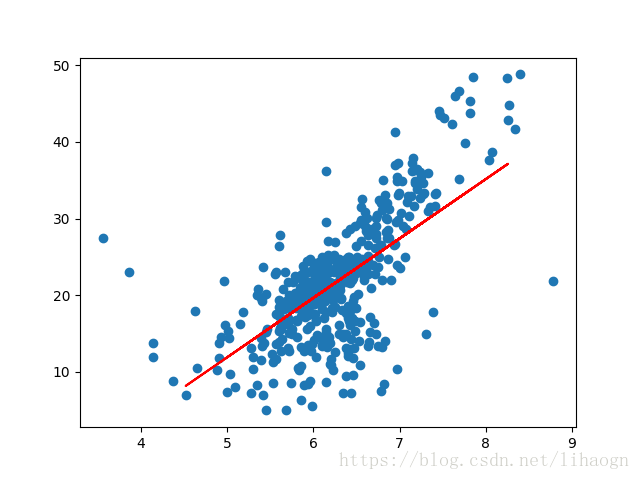
# 3 绘制出线性关系
plt.plot(x_test, slr.predict(x_test), color="red")
plt.show()

运行结果：

['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
 'B' 'LSTAT']
(506,)
(506,)
0.5857523540718015

4）test1.py

from sklearn import datasets
from comm_utils.model_selection import train_test_split
import LinearRegression_pro.LinearRegression

# 准备数据，波士顿房产数据
boston = datasets.load_boston()

x = boston.data
y = boston.target

x = x[y < 50.0]
y = y[y < 50.0]

print(x.shape)
print(y.shape)


# 使用线性回归法

# 1 拆分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y)
# 2 拟合
slr = LinearRegression_pro.LinearRegression.LinearRegression()
slr.fit_normal(x_train, y_train)
# 3 测试性能
print(slr.score(x_test, y_test))

运行结果：

(490, 13)
(490,)
0.7327444560557277

5 总结

• 典型的参数学习，kNN是非参数学习
• 只能解决回归问题
• 对数据有假设：线性
• 对数据具有强解释性

最后

以上就是眯眯眼小甜瓜为你收集整理的机器学习入门 03 线性回归法（Linear Regression）的全部内容，希望文章能够帮你解决机器学习入门 03 线性回归法（Linear Regression）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。