机器学习 （十） 优化算法利器之梯度下降（Gradient Descend）前言数学概念-梯度机器学习中梯度应用实战优化疑问总结题外思考

理解：机器学习各种算法的求解最终出来的几乎都是求解最优模型参数的优化问题。

前言

       在优化问题领域有些很多优秀思想和算法，从约束条件分类 分为无约束条件的优化和有约束条件的优化问题，有约束条件优化分支里面又分为了等式约束条件和不等式约束条件，想不想逐一了解一下，本篇博客让我们一起来看一下无约束条件的算法之一，叫做梯度下降 (GD)。

数学概念-梯度

       求导是高中数学上层中的内容，想必大家都有所耳闻，没有把所有数学还给老师，其实对于数学不好的同学可以自己买两本书回顾一下，我们没有学好数学也不能怪咱们学的不好，只能说是那个老师没有教好，学的时候是为了应付考试不知道数学的重要性，自从干上机器学习感觉数学的价值发挥出来了，每一个概念和公式都是那么熠熠生辉、流光溢彩，觉的是前人发明这个概念是顺其自然 同时也赞叹前辈们智慧超能的大脑，竟然发明出来了这么多概念，以后又非常重要。
       现在我们求y=x^2的导数，大家一看 为f’(x)=2x ,计算非常快，不过对于数学概念最大的误区就是不能死记公式，一定要理解求导以及导数的定义以及意义，如此在数学领域才能一步步走的更远。

定义：
导数（Derivative）是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’(x0)或df(x0)/dx。

       从定义可以看出来导数表示的是因变量增量Δy和自变量增量Δx的比值，也就是自变量变化一点点时因变量变化了多少，表示因变量随自变量变化的快慢程度，正规一点表示就是一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部（某点）的线性逼近。
       生活中复杂的事物比简单的事物多，如果自变量变为2维、3维甚至更多时，这个导数如何求得，令其它自变量为常数，分别对各个维度单独求导数即偏导数，对某个点的变化率引入新的概念叫做梯度，可以理解梯度是导数的升华和抽象，是为了在多维空间描述多维空间函数变化快慢程度的量，它是一个向量，沿着梯度的方向移动是函数变化最快的方向，先看下定义：

来看一下梯度的直观解释，如下图：

       假设三维空间函数的几何空间图形如上所示，我们现在要找到全局最小值，该怎么样求解呢？大家最常想到的是求导 令导数为零，这是一种方法，只是如果导数不能够求出来时就不太管用了，我们可以用梯度下降法来求解，梯度即高维空间的导数可以看成是函数图形坡度变化的速率，理论上无论沿着哪个方向都可以找到最小值，无非在图形上多转几圈，需要持续大量计算，如果想尽可能快的找到最优的下坡路线图，那么需要借助于梯度大小来确定，每次都朝着梯度最大值方向移动可见是最陡的路走，下坡将会非常快。

       从图中还可以看到出现了两条路径，此问题也很好理解，设想你在一座山上，下山的路众多，你可能从山顶一下能看到最优的下山路线，但是计算机并不知道它没有眼睛，我们告诉它的规则是哪里陡峭就走哪里的思路，你觉得它一定能安全的山下吗？如果最陡峭的地方连着另一个山就走不出去了，到了一个局部最小点那里，因此单纯的梯度下降是很难找到全局最优值得。

       在解决这类极值问题的时候，我们往往想让函数为凸函数，这样梯度算法找出来的结果就是全局最优值，在解决实际问题时 我么的损失函数是否为凸函数呢？这就需要知道啥叫凸函数，在数学上有定义和定理，如果一个函数的海森矩阵是正定的它就是凸函数，还有啥半正定、行列式、主子式等等，涉及的数学知识较多，发现很多的实际问题模型，背后都离不开数学理论的支持，可以说数学是一门凝缩精华的学科，掌握了数学即可掌握世界的发展。

机器学习中梯度

       在机器学习中，哪里可以用到梯度求解算法呢，其实哪里都可以用到只要求解最优值问题都可以将梯度方法用上，不过最常用的地方还是是求解损失函数的最小值，通过损失函数最小值求出来模型参数，损失函数一般代表着设计模型和真实值之间误差多少的代表，从理论上来说 不考虑结构化风险 这个误差当然是越小越好，这就引出了梯度求解损失函数最优值问题，每个模型原理和复杂度不一样表达式也不一样，本质是一样的最优值问题。

应用实战

       在机器学习实战一书中，逻辑回归里面再求最小误差公式时，利用梯度上升算法来求解，本质和梯度下降是一样的东西，有多少个样本就对模型参数训练了多少次，主要代码如下：

def stocGradAscent0(dataMatrix,classLabels):
    '''
        获取最佳拟合参数向量
    :param dataMatrix:数据集
    :param classLabels:类别标签
    :return:最佳拟合参数向量
    '''
    m,n = np.shape(dataMatrix)
    print "m = %s,n = %s " % (m,n)
    # 步长
    alpha = 0.01
    # 初始化拟合参数向量
    weights = np.ones(n)
    print "weights %s = " % weights
    # 对回归系数进行样本数量的梯度上升，每次仅仅使用一个样本
    for i in range(m):
        print "dataMatrix[i] = %s" % dataMatrix[i]
        # h为单一样本的预测结果
        h = sigmoid(sum(dataMatrix[i] * weights))
        # error为单一样本的误差
        error = classLabels[i] - h
        # 根据单一样本结果来更新回归系数
        weights = weights +alpha * error * dataMatrix[i]
    return weights

在求解的时候通常利用矩阵进行计算，简介明了，矩阵包含的信息多看起来就简单，简单唯美。

优化

       步长(learning rate):即每次走的时候朝着梯度方向走多远，梯度是一个向量，给我们确定走路的方向和大小，但是需要走向量的多少需要我们自己来确定，这个是一个可以持续优化的参数，步长选取是否合理对求解结果也会有影响。

       损失函数(loss function):为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。
在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本（xi,yi）(i=1,2,…m),采用线性回归，损失函数为：

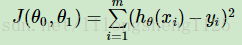
　　　　其中xi表示第i个样本特征，yi表示第i个样本对应的输出，hθ(xi)为假设函数。
根据训练模型时样本个数分类如下：
- 批量梯度下降（Batch Gradient Descent)
言简意赅批量的意思是样本一批一批传给模型，让模型从中训练模型参数，如果有10万样本一次给模型5万，两次即可完成训练过程，即求解两次梯度如此求出来的结果很可能不太准确
- 随机梯度下降 (Stochastic Gradient Descent)
随机梯度下降是每次采用一个样本来进行训练模型，假如10万个样本点那么得训练10万次，次数变多了像目标收敛的速度自然就变短了，训练速度加快，因为模型一般是利用矩阵来进行计算，随着样本增多矩阵会越来越大，矩阵非常大时速度就会变慢。
小批量梯度下降 (Min Batch Gradient Descent)
此种方法介于批量和随机梯度之间，样本个数分成了很多小份来不断更新模型，好像这种模式更常用一些，类似于交叉验证，这也让我联想到这中庸之道旨在于一个中和问题，在生活中同样是这种道理凡是不能走极端，采取双方都收益实现双赢的局面才是最好的。

疑问

梯度法与最小二乘法区别 ？

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

在我们得到我们的损失函数时正好也是利用了这一点，误差平方和最小原理，出来了我们的损失函数，
梯度法是迭代法的一种，可以解决各种最优化问题（包括最小二乘问题），也可以翻过来理解，即如果把最小二乘看做是优化问题的话，那么梯度下降是求解方法的一种。
最小二乘还有狭义和广义之分，
线性回归的模型假设，这是最小二乘方法的优越性前提，否则不能推出最小二乘是最佳（即方差最小）的无偏估计，具体请参考高斯-马尔科夫定理。特别地，当随机噪声服从正态分布时，最小二乘与最大似然等价。

关于计算
计算一个矩阵的逆是相当耗费时间的, 而且求逆也会存在数值不稳定的情况 因而这样的计算方法有时不值得提倡.相比之下, 梯度下降法虽然有一些弊端, 迭代的次数可能也比较高, 但是相对来说计算量并不是特别大. 而且, 在最小二乘法这个问题上, 收敛性有保证. 故在大数据量的时候, 反而是梯度下降法 (其实应该是其他一些更好的迭代方法) 更加值得被使用.。

总结

       梯度下降算法是众多优化算法中的一个，他的原理是顺着梯度方向逐步迭代求解，一步一步像最优解靠近最终得到最优解的过程，在算法解法中如动态规划、贪心算法其实好多地方用到了迭代的方式解题，这种方式效率高，比普通的循环要高一些，在函数式编程中大部分利用这种思想来编写程序，还是老套路在学习一个算法的时候要懂得这个算法是如何来的？在哪里应用以及局限性，这样才能灵活应用避免接触的算法多了变得一头雾水，思路不清晰。

题外思考

货币的起源和其特性？
       这还要从历史说起，回到远古时代人们过着狩猎的生活，随着生活有了规律屋子逐渐丰富起来，粮食等有了剩余，但是发现缺少其它东西比如香皂等，这时人们就想将自家的粮食和别人交换，最开始只是拿一些易于保存、有特征的东西当做交换的凭证，比如大石头，后来经过不断发展产生了大家公认的货币，其实货币概念要某个首领或者权威部门公式，只有大家都知道它代表这个等价的物品，别人才买你的账，才可能和你交换，就如同现在的人民币，再说说支付宝其实也是一个货币工作，在它里面展示的只是一个数字而已，你却可以用它来买卖这种东西，这种即货币的作用，其实货币正在向着数字化方向发展，我感觉自己已经很久没有使用纸币了，有时拿着一点也是为了手机没电或者特殊情况备用，日常消费往往一部手机足以。
代表货币的工具、表现方式并不重要，重要的是它所公认的属性所发挥的作用。

最后

以上就是感动皮带为你收集整理的机器学习 （十） 优化算法利器之梯度下降（Gradient Descend）前言数学概念-梯度机器学习中梯度应用实战优化疑问总结题外思考的全部内容，希望文章能够帮你解决机器学习 （十） 优化算法利器之梯度下降（Gradient Descend）前言数学概念-梯度机器学习中梯度应用实战优化疑问总结题外思考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。