概率生成模型

前言

来源：

• 视频：李宏毅2020机器学习 – classification_1

• 作业代码：Porbabilistic generative model

• 课件：Classification: Probabilistic Generative Model

• 其他人的笔记：Classification: Probabilistic Generative Model

我之前用线性回归，做上课机器学习的作业。小于0.5的作为一类，大于0.5的为另一类。我不知道这样做方法的好坏(准确率73%左右)，但作业确实这样交了。嘿嘿。

使用线性回归做分类问题，并非一个好的解决方法。因为如下图所示。好的分类是绿色的直线，但使用线性回归得到的却是紫色的直线。

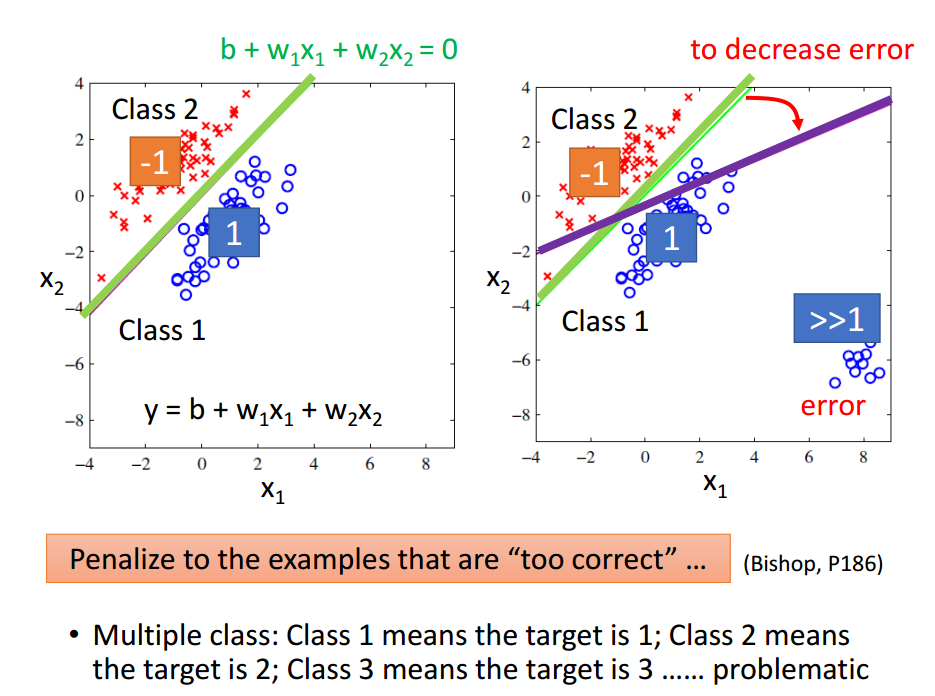
所以，下面介绍，使用概率生成模型进行分类。

生成模型

假设，我们需要将数据进行分类两类。[分成多类和两类的思考过程相同。我们使用两类进行说明。]

假设分为两类的球，分别占比2/5和3/5。这时候拿一个新的球儿过来，预测它属于哪一类。假如我们什么信息都不知道，肯定选认它是3/5的那一类。这样概率会比较大。

假如，我们知道具体的数据信息，如下图所示。Class 1中四个篮球，一个绿球。Class 2中两个篮球，三个绿球。对于一个给定的球，判断它属于哪一类，则应该使用下图中的公示。[另外是不是感觉哪里不对劲，为什么不把蓝色的球放在一个class中，绿色的球放在一个class中。我这样认为：蓝色和绿色是不同的属性，class是不同的标签。属性和标签之间有联系，但并不是必然联系。虽然属性相似，但是在不同的标签中。]

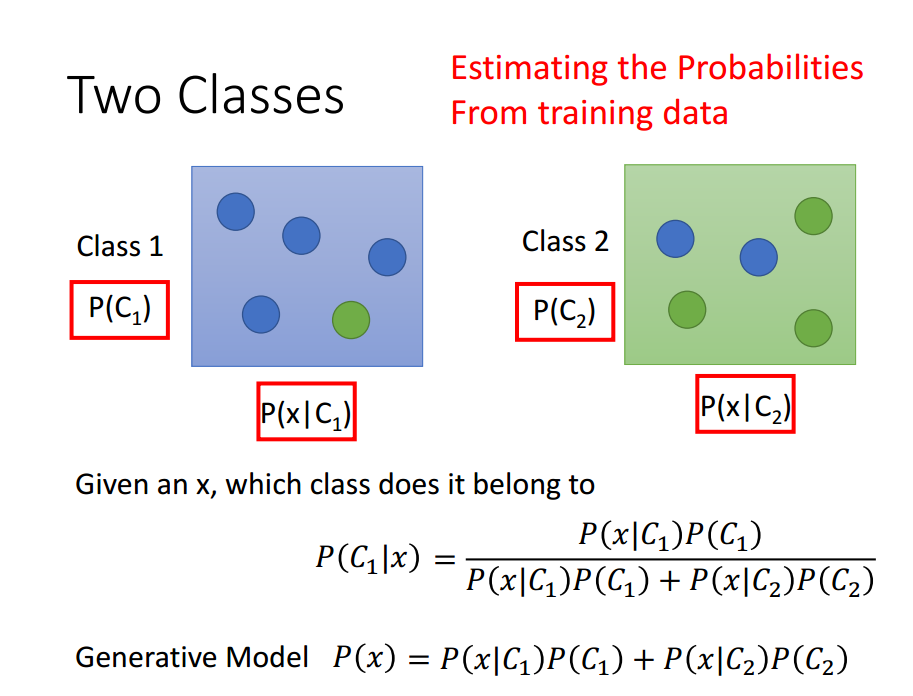
上面的P(blue|C_1)=4/5，P(green|C_1)=1/5。但是此时拿过来一个蓝绿色的球，问是哪一类的？我们不可以说没有这一类，因为这一类确实存在，只是我们的测试数据中不存在而已。所以，我们还需要知道数据的分布。根据已有的数据，计算出具体的分布函数。

我们使用高斯分布进行说明，其他分布说明过程类似。
$$f_{\mu ,\Sigma }(x)=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{|\Sigma {|}^{1/2}}\exp \left\{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right\}$$
任意一个具体的高斯分布函数，都可以满足数据。但是我们希望得到的????(均值)和Σ(协方差) ，可以是最符合这组数据的高斯分布函数。其中????和Σ 如下计算。

此时，我们分别计算两类数据的高斯分布，结合两类数据个数的比例，便可以预测一个测试数据属于哪一类。

修改生成模型

改进模型，使两类数据共用同一个协方差，均值不变。这里的协方差由两个类的协方差加权求和构成。[参数过多，多拟合？]

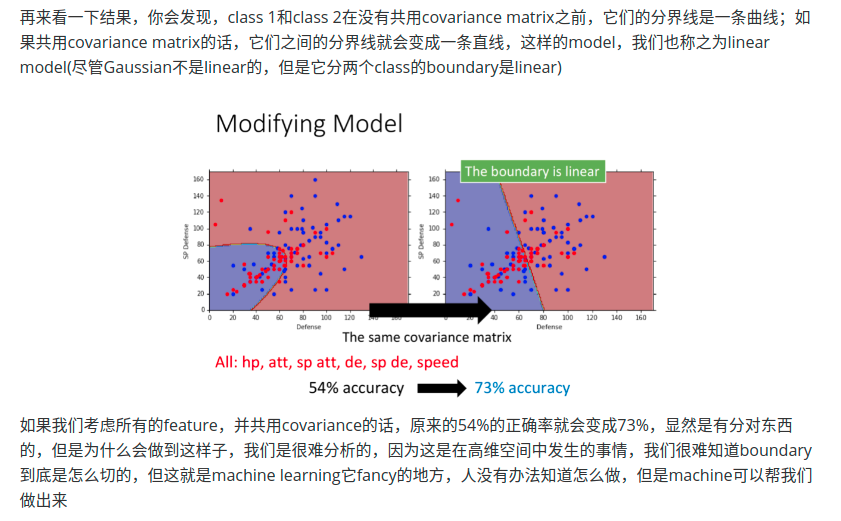
模型转换

概率生成模型的决策函数可以转换成sigmoid函数。

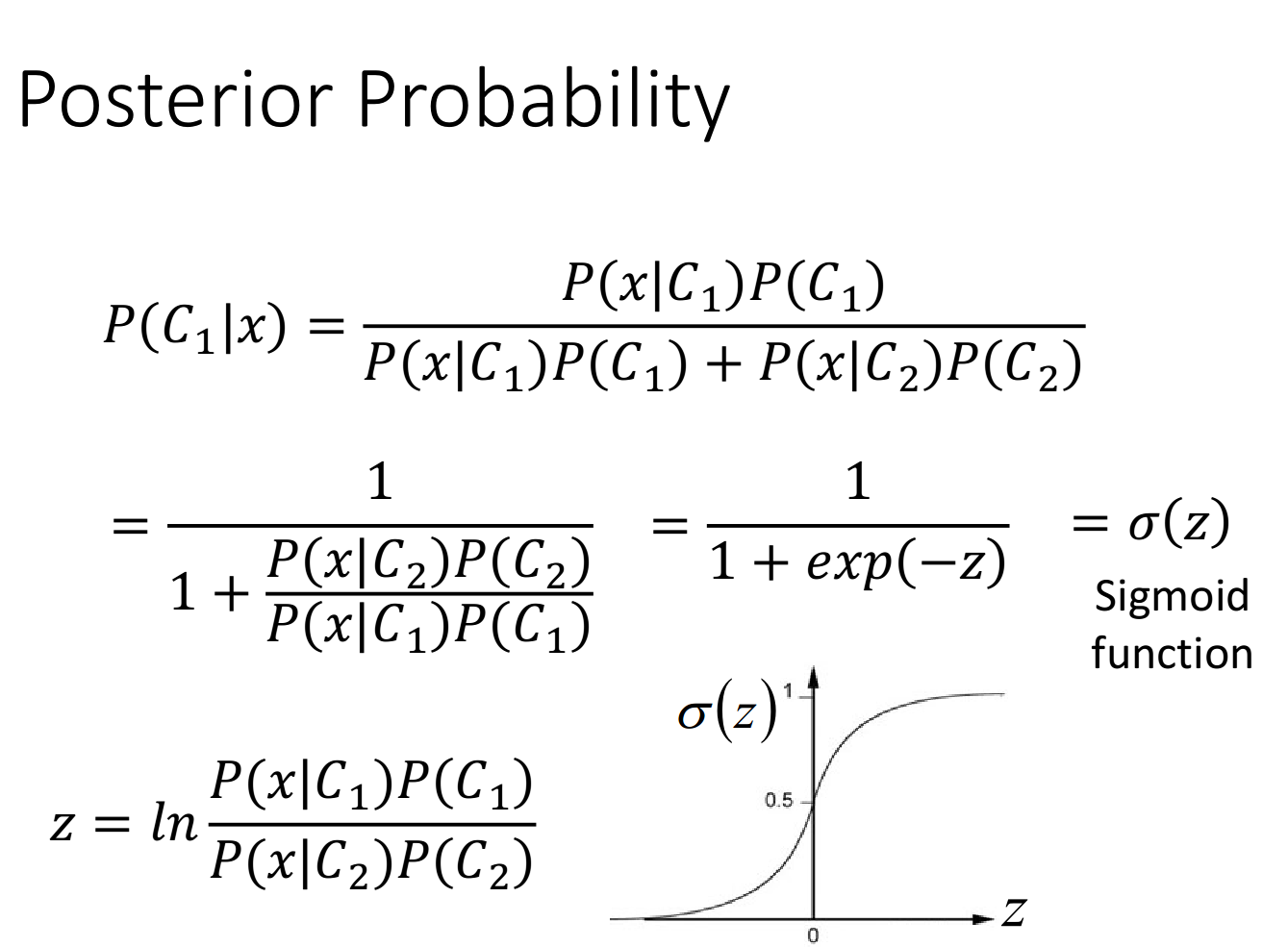
经过一串推导，得到如下结果。

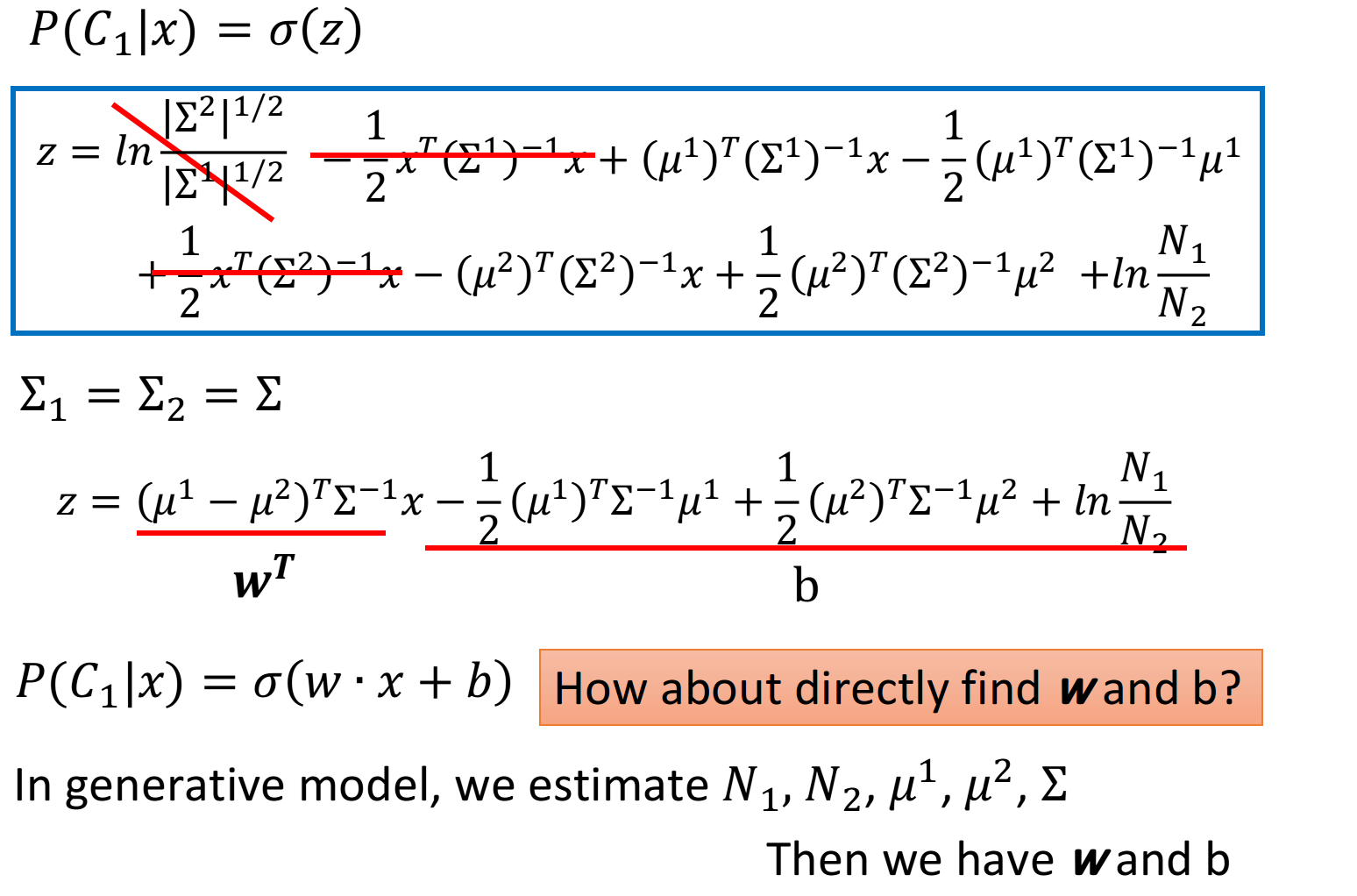
所以我们能不能直接把w和b找出来呢？这是下一章节的内容。

代码实现

# Compute in-class mean
X_train_0 = np.array([x for x, y in zip(X_train, Y_train) if y == 0])
X_train_1 = np.array([x for x, y in zip(X_train, Y_train) if y == 1])

# 计算均值
mean_0 = np.mean(X_train_0, axis = 0)
mean_1 = np.mean(X_train_1, axis = 0)  

cov_0 = np.zeros((data_dim, data_dim))
cov_1 = np.zeros((data_dim, data_dim))
# 计算不同类的协方差
for x in X_train_0:
    cov_0 += np.dot(np.transpose([x - mean_0]), [x - mean_0]) / X_train_0.shape[0]
for x in X_train_1:
    cov_1 += np.dot(np.transpose([x - mean_1]), [x - mean_1]) / X_train_1.shape[0]

# 共享协方差被视为单个类内协方差的加权平均值
cov = (cov_0 * X_train_0.shape[0] + cov_1 * X_train_1.shape[0]) / (X_train_0.shape[0] + X_train_1.shape[0])

如果不打算转换模型，可以这一步便计算，测试用例属于不同类中的概率，然后选最大值就好。

如果转换模型，计算w和b的话，加上如下代码。这是二分类，所以计算出x在class 1中的概率大于0.5，则属于class 1。否则，则属于class 2。如果是多分类的话，怎么办？

u, s, v = np.linalg.svd(cov, full_matrices=False)
inv = np.matmul(v.T * 1 / s, u.T)

# Directly compute weights and bias
w = np.dot(inv, mean_0 - mean_1)
b =  (-0.5) * np.dot(mean_0, np.dot(inv, mean_0)) + 0.5 * np.dot(mean_1, np.dot(inv, mean_1))
    + np.log(float(X_train_0.shape[0]) / X_train_1.shape[0]) 

最后

以上就是糟糕蛋挞为你收集整理的概率生成模型的全部内容，希望文章能够帮你解决概率生成模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。