基于RNN的加法运算器-从零实现循环神经网络一　数据集准备二　初始化模型参数三 定义模型四 定义预测函数五　困惑度六　定义模型训练函数七　有意思的实验参考

本文以一个简单的RNN为例，训练一个可以做二进制加法的循环神经网络．

一　数据集准备

准备了一个二进制加法的数据集．其数据范围是0-255，即最大值为$2^8-1=255$. 正数的加法如下，比如 c = a + b = 1 + 2 = 3; 对应到二进制的加法如下：$a=[00000001];b=[00000010];c=[00000011]$. 根据我们的经验，二进制加法和的位置ｔ的值其实不仅依赖于ａ与ｂ在ｔ位置的值，还依赖于前几位的情况，如t-1, t-2…因此理论上来看，卷积神经网络应该可以很好地处理这种场景，我们的目标就是输入ａ，ｂ，得到ｃ（均为二进制）．
代码：运行cal_generate_data, 可以生成数据．生成的数据结构，使用pickle，将其序列化为二进制，使用的时候将其调出即可使用（类似matlab下的.mat)
one-hot向量表示法．这里需要注意的是，我们的神经网络在输入时，单个时间步的输入其实是[0，0],是一个２＊１的向量，词典中不同的字符个数为2（即不同的字符只有0, 1,因此词典大小为2)

二　初始化模型参数

隐藏单元个数，隐藏单元个数是一个超参数，超参数是在在机器学习中，需要提前定义的参数，而不是通过学习得到的参数．这里，我们将该超参数设置为16．
输入．输入的个数是由词典的维度决定的，这里我们的维度为２，因此输入为２＊１.
输出．同输入，输出的个数也是由词典的维度决定的，这里为２＊１
根据输入输出以及隐含单元，我们就可以确定网络结构如下：

1. 历史状态值St: 16 $\times$ 1
2. 变量权重值U 16 $\times$ 2
3. 历史权重值Ｗ16 $\times$ 16
4. 输出权重值Ｖ2 $\times$ 16
   

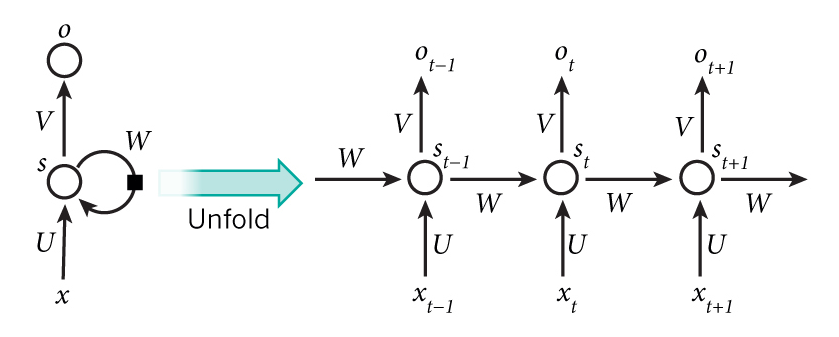
三 定义模型

隐含状态的存储．为了方便多个时间步信息的存储，我们将UVW保存在Model这个类中. 将计算出来的历史状态信息，即每一层的信息，保存在layers类中，在该例中，我们应该有８个时间步，保存８个layer的信息.

四 定义预测函数

predict函数.predict的过程，就是输入一个８＊２的ｘ，得到一个８＊１的标签.在每一个时间步上，进行前向传播．然后将结果分类为０－１．通过如下：argmax(output.predict(layer.mulv))；维度变化：21–>21–>1；其中，output.predict使用exp指数函数把数值映射到正数空间，然后对其归一化．

五　困惑度

六　定义模型训练函数

1 损失函数

首先使用predict函数，得到０｜１的概率. 即０｜１的概率分别为：probs＝0.4|0.6．
假设此时标签为y=1, 那么loss = -np.log(0.6); 我们希望0.6越大越好．

2 梯度

• diff函数．与损失函数一样，得到probs, [0.4, 0.6]．然后y = 1, probs[1] - 1. 因为其第二个位置就是应该等于１．最小化[0.4, - 0.4] 的平方．相当于要最小化上面的值的绝对值，使其最优值等于０．
• 基于时间的后向传播定律．整个的变量只有三个：ＵＶＷ，我们只需要得到偏导数即可dU, dV, dW．输入x,与y ．利用前向传播，计算每一层的中间变量.对于时间步１，计算其对于U,V,W的误差．对于时间步２，计算其对ＵＶＷ的误差，同时加上时间步１的误差．依次类推．

3 训练

生成测试集合：运行：　cal_generate_data．训练．然后测试．

七　有意思的实验

实验１，加法顺序对模型的影响

• 采用逆序加法．这是人做加法的自然顺序，位低的数值会影响到位高的数值．训练的结果如下：

2019-07-16 17:21:53: Loss after num_examples_seen=0 epoch=0: 0.711610
2019-07-16 17:22:22: Loss after num_examples_seen=20000 epoch=1: 0.056623
2019-07-16 17:22:51: Loss after num_examples_seen=40000 epoch=2: 0.034568
2019-07-16 17:23:20: Loss after num_examples_seen=60000 epoch=3: 0.031605
2019-07-16 17:23:49: Loss after num_examples_seen=80000 epoch=4: 0.030482
2019-07-16 17:24:17: Loss after num_examples_seen=100000 epoch=5: 0.029896
2019-07-16 17:25:04: Loss after num_examples_seen=120000 epoch=6: 0.029538
2019-07-16 17:25:51: Loss after num_examples_seen=140000 epoch=7: 0.029297
2019-07-16 17:26:37: Loss after num_examples_seen=160000 epoch=8: 0.029123
2019-07-16 17:27:25: Loss after num_examples_seen=180000 epoch=9: 0.028993

准确率 100%

• 采用从左向右，数组自然顺序
  从直觉上讲，这样是不行的，因为加法的法则就是从右向左，历史信息保存在右边．这样其实拿不到历史信息．
  训练结果如下：

2019-07-16 19:59:14: Loss after num_examples_seen=0 epoch=0: 0.709881
2019-07-16 20:00:30: Loss after num_examples_seen=20000 epoch=1: 0.658799
2019-07-16 20:01:50: Loss after num_examples_seen=40000 epoch=2: 0.622423
2019-07-16 20:03:09: Loss after num_examples_seen=60000 epoch=3: 0.617654
2019-07-16 20:03:39: Loss after num_examples_seen=80000 epoch=4: 0.614902
2019-07-16 20:04:08: Loss after num_examples_seen=100000 epoch=5: 0.612439
2019-07-16 20:04:38: Loss after num_examples_seen=120000 epoch=6: 0.610115
2019-07-16 20:05:08: Loss after num_examples_seen=140000 epoch=7: 0.608214
2019-07-16 20:05:37: Loss after num_examples_seen=160000 epoch=8: 0.606709
2019-07-16 20:06:07: Loss after num_examples_seen=180000 epoch=9: 0.605867

准确率84％
从该实验可以看出，ＲＮＮ的确是使用了历史信息，才使得模型比较准确．通过训练学习到了二进制加法的规则．从侧面反应了如下论断：

1. 凡是结构化，规则化的任务，配合大量数据，使用深度学习方法要优于传统方法．
2. 只要隐含层足够大，神经网络可以模拟任何非线性函数．

代码：
https://github.com/junwangcas/blogs/tree/master/01RNN/01_additional_example

参考

1: 一个使用attention模型，在karas中可视化训练的模型 https://medium.com/datalogue/attention-in-keras-1892773a4f22
2: karas官方自带的求和的例子：https://keras.io/examples/addition_rnn/　
3: https://github.com/pangolulu/rnn-from-scratch

最后

以上就是淡淡小土豆为你收集整理的基于RNN的加法运算器-从零实现循环神经网络一　数据集准备二　初始化模型参数三 定义模型四 定义预测函数五　困惑度六　定义模型训练函数七　有意思的实验参考的全部内容，希望文章能够帮你解决基于RNN的加法运算器-从零实现循环神经网络一　数据集准备二　初始化模型参数三 定义模型四 定义预测函数五　困惑度六　定义模型训练函数七　有意思的实验参考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。