linear regresssion

之前利用感知机演算法，我们可以在二元分类问题上进行机器学习。现在我们将探究输出空间为实数时，如何实现机器学习？
一、linear regression 准备工作
先假设vc bound对回归问题是成立的，因此我们来设计一个简单的演算法。对于演算法，我们需要训练集，hypothesis set，E_in（h）。来看看hypothesis：
我们可以将hypothesis设定为特征的加权和。
给定训练集和hypothesis set ，我们能做些什么呢？最好的hypothesis 有什么几何意义呢？如何pick最好的hypothesis？

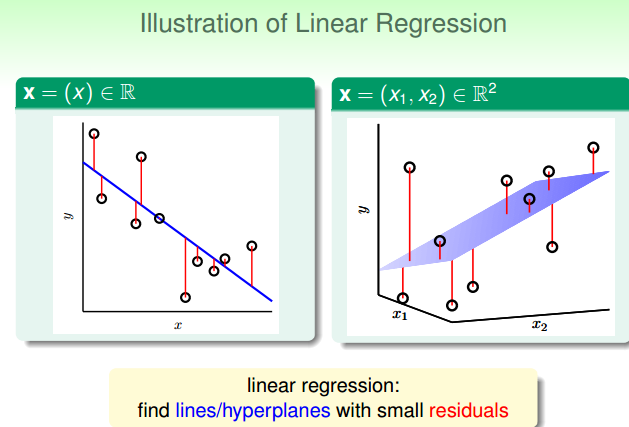
从上图可以看出，最好的hypothesis 和训练集中所有样本的残差和最小，别忘了，我们演算法的目的是使得E_in越小越好。error measure最基础的形式分为0/1error和 squared error，根据上图，我们应该选择squared error来描述E_in，可以写出其表达式。

二、如何最小化E_in（w）
将E_in（w）表达为矩阵形式，这是因为我们不希望表达式中夹杂着求和符和样本索引。各个分量先平方再求和，这不正是向量长度的定义吗？！因此可以使用向量长度平方来表达当前这个表达，此时表达式中，只有w向量是未知的。

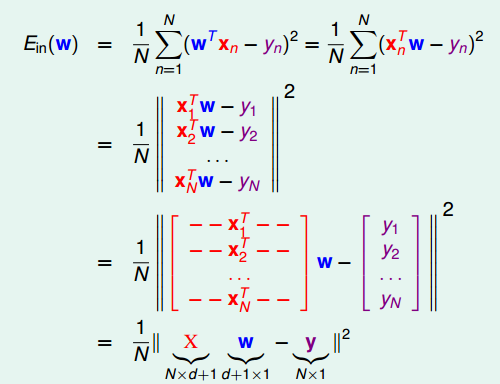
数学上可证明这个E_in(w)函数是个convex，连续，可微的，由于是convex，因此最小的函数值处的梯度为0。先计算向量长度平方得到一个表达式，再来求梯度并使其为0，可得到w的表达。

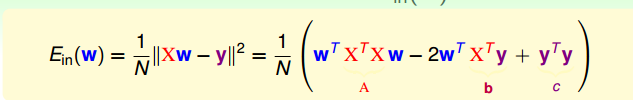
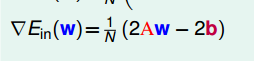
因此，最优的w可通过一个给定的表达式就可求出，不但很快可求出，还能保证当前的w使得E_in（w）是最小的。来回顾一下，做线性回归，我们需要哪些步骤？有了资料代入计算公式就可求得w，进而可得hypothesis 。我们称这种利用公式就可求得最优的hypothesis的方法为analytic solution，此时只要保证hypothesis的d_vc是有限的，我们就可以说机器学习已经发生啦！

这里给出另一种方法证明E_out（w）很小，计算多笔资料的平均值E_out（w）。与之对应的有E_in（w）的平均值。（E_out（w）均值的推导较E_in（w）均值更为复杂，因此我们只推导E_in（w）均值）
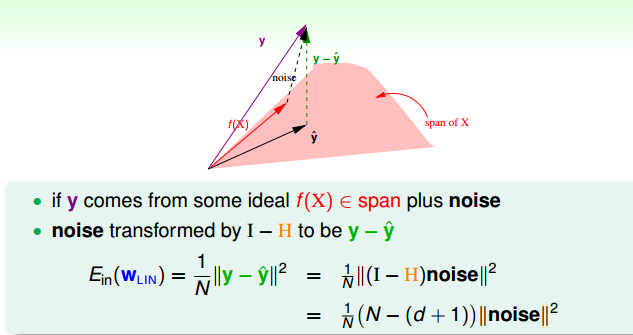E_out（w）均值大于E_in（w）均值，N很大的时候E_out（w）确实很小。而且E_out（w）均值和E_in（w）均值保持在一定的差距范围内，证明泛化能力得到了保证。而且从下图可以看出E_in是0的时候，E_out却不一定是最好的。


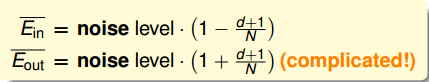
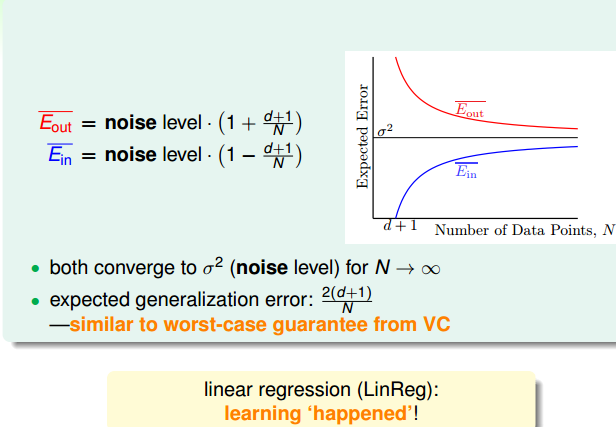
四、能否使用linear regression 来做binary classification
对于binary classification问题，我们先前使用PLA或是pocket 算法，但这个属于NP-HARD问题。而linear regression 属于analytic problem，能够迅速求得解，二元分类的取值被限定在1和-1之间，而regression的取值是全体实数，所以使用回归算法求解二元分类问题理论上可行吗？

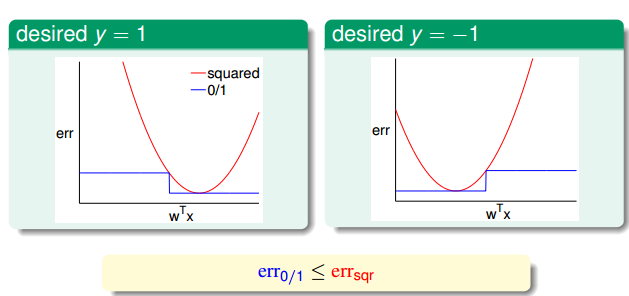
比较两种方法的演算法，最大的差别在于，错误度量函数不一样。那么这两种error function是否存在一定的大小关系呢？对于二元分类，可以验证err_squared总是大于err_0/1。使用而缘分类的vc bound公式，我们对其E_in进行缩放（E_in就是使用err表达的），因此有下式成立，所以当我们使用regression模型时，只要能保证E_in（h）足够小。我们也就能保证E_out（h）足够小，所以回归模型可以用来解决二元分类问题。

最后

以上就是文艺小刺猬为你收集整理的linear regresssion的全部内容，希望文章能够帮你解决linear regresssion所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。