【菜鸡刷题-牛客网NC68】青蛙跳台阶 | 斐波那契数列 | 二叉树 | 递归实现 | 迭代实现 | python题目描述抓重点题分析递归实现 - 不推荐迭代实现斐波那契数列 - ⭐ 推荐 ⭐

103 阅读 0 评论 68 点赞

概述

@author = yhr | 若需要转载，请标明本文来源！

文章目录

题目描述
抓重点
题分析
递归实现 - 不推荐
迭代实现斐波那契数列 - ⭐ 推荐 ⭐

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。
求该青蛙跳上一个n级的台阶总共有多少种跳法？
（先后次序不同算不同的结果）
以 N=5 为例，输出 8 种路径。

抓重点

题目理解为：

从0开始，每次+1或者+2，有几种方式可以得到N？
以 N=5 为例，输出 8 种路径。

那么可以反过来理解为：

从N倒退，每次-1或者-2，有几种方式可以得到0？
以 N=5 为例，输出 8 种路径。

题分析

由于每次只有两种选择：走1，或者走2，那么可以写成一个二叉树：

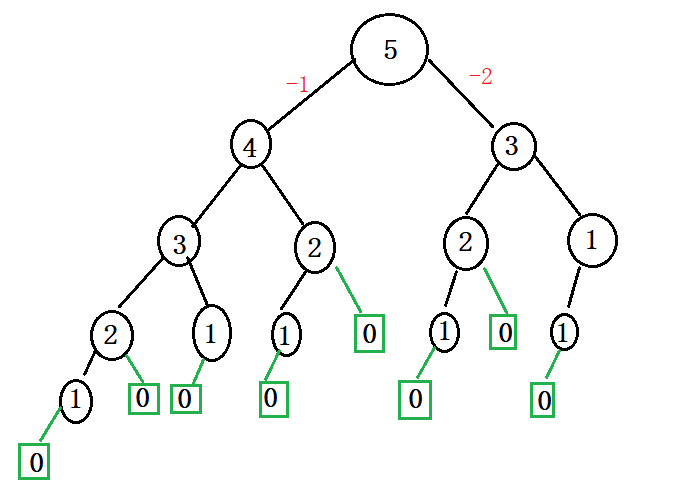
在这里插入图片描述

然后发现：

5 到 4，只有一种走法，即-1。
5 到 3，只有一种走法，即-2。

得出结论：

N 到 N-1 ，只有一种走法，即-1。
N 到 N-2 ，只有一种走法，即-2。

那么用递归的思路来看：

N到0 的路径数 = N-1到0 的路径数 + N-2到0 的路径数。

即左右子树的路径之和。

用 F(N) 表示 N 到 0 的路径数目，那么以上结论可以写成如下公式：

					F(N) = F(N-1) + F(N-2) 
					F(2) = 2    # 2 到 0 有两种方式： a. 2-2   b. 2-1-1
					F(1) = 1    # 1 到 0 有一种方式： a. 1-1

是不是很眼熟，没错，他就是斐波那契数列形式的数列！

递归实现 - 不推荐

 def fibonacci_loop(self, number):
        if number == 1:
            return 1
        elif number == 2:
            return 2
        else:
            return self.fibonacci_loop(number-1) + self.fibonacci_loop(number-2)

迭代实现斐波那契数列 - ⭐ 推荐 ⭐

参照以下博客的第二种方法：
斐波那契数列（四种解法）

front 表示相对来说第二项的内容
later 表示相对来说第一项的内容

front = front + later // 此时 front 变成第三项的内容。
later = front - later // 此时 later 变成第三项 - 第一项内容的内容 = 第二项的内容。
此时 later仍然是相对来说第一项的内容， front 表示相对来说第二项的内容。
later, front 迭代往前推进

def fibbonacci(self, number):
        frontV = 1; laterV= 1
        for _ in range(2, number+1):
            frontV = frontV + laterV;  
            laterV = frontV - laterV; 
        return frontV