CodeTop每日系列三题------------------2021.12.8

59 阅读 0 评论 39 点赞

我是靠谱客的博主眯眯眼花卷，最近开发中收集的这篇文章主要介绍CodeTop每日系列三题------------------2021.12.8，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

LC198. 打家劫舍
//经典的动态规划的题目，dp的状态转移方程想出来了，但是dp没有初始化成功，还是不熟。
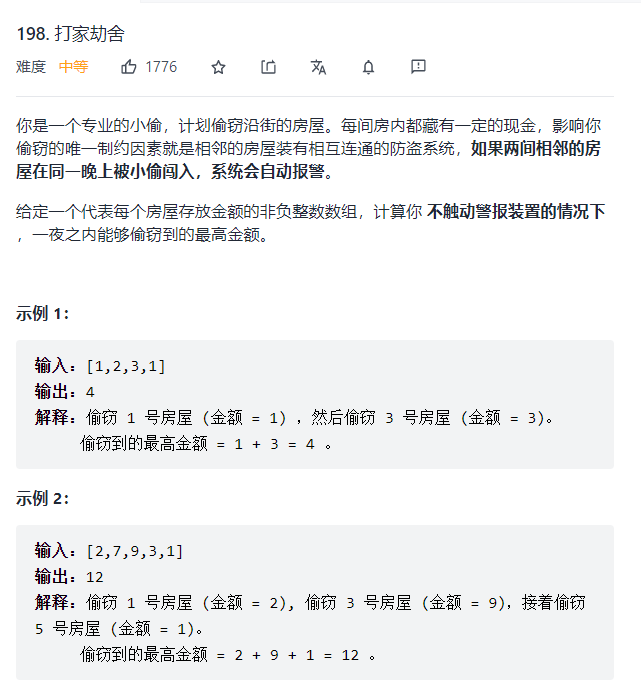
在这里插入图片描述

class Solution {
    public int rob(int[] nums) {
        if(nums == null || nums.length == 0)
        return 0;
        if(nums.length == 1)
        return nums[0];
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);
        for(int i = 2;i < nums.length;i++){
            dp[i] = Math.max(dp[i - 2] + nums[i],dp[i - 1]);
        }
        return dp[nums.length - 1];
    }
}

在这里插入图片描述
LC移动0
//双指针，一个指针指向0的位置一个指针指向非0的位置，同时特性也要注意当右指针指向到非0 元素那么之前的元素都是0，左指针元素前边的都是非0元素。

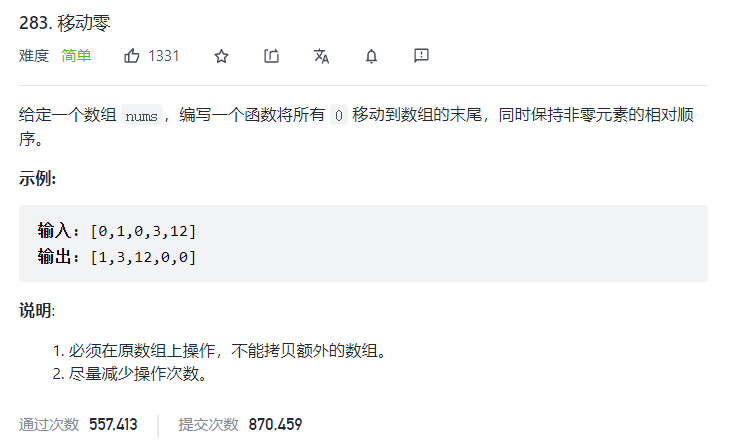
class Solution {
    public void moveZeroes(int[] nums) {
        //双指针left指向0的位置，right指向非0位置
        int n = nums.length,left = 0,right = 0;
        while(right < n){
            //遇到非0的元素
            if(nums[right] != 0){
                //进行交换
                swap(nums,left,right);
                //同时也有个特性就是非0前面的元素都是0那么只需要left++即可
                left++;
            }
            right++;
        }
    }

    public void swap(int[] nums,int left,int right){
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }
}

在这里插入图片描述
LC剑指 Offer 10- II. 青蛙跳台阶问题
//变种斐波那契问题和LC剑指 Offer 10- I. 斐波那契数列异曲同工之妙，就是改变初始值即可。

class Solution {
    public int numWays(int n) {
        int a = 1,b = 1,sum = 0;
        for(int i = 0;i < n;i++){
            sum = (a + b) % 1000000007;
            a = b;
            b = sum;
        }
        return a;
    }
}