d2 链表 easy
35. 复杂链表的复制
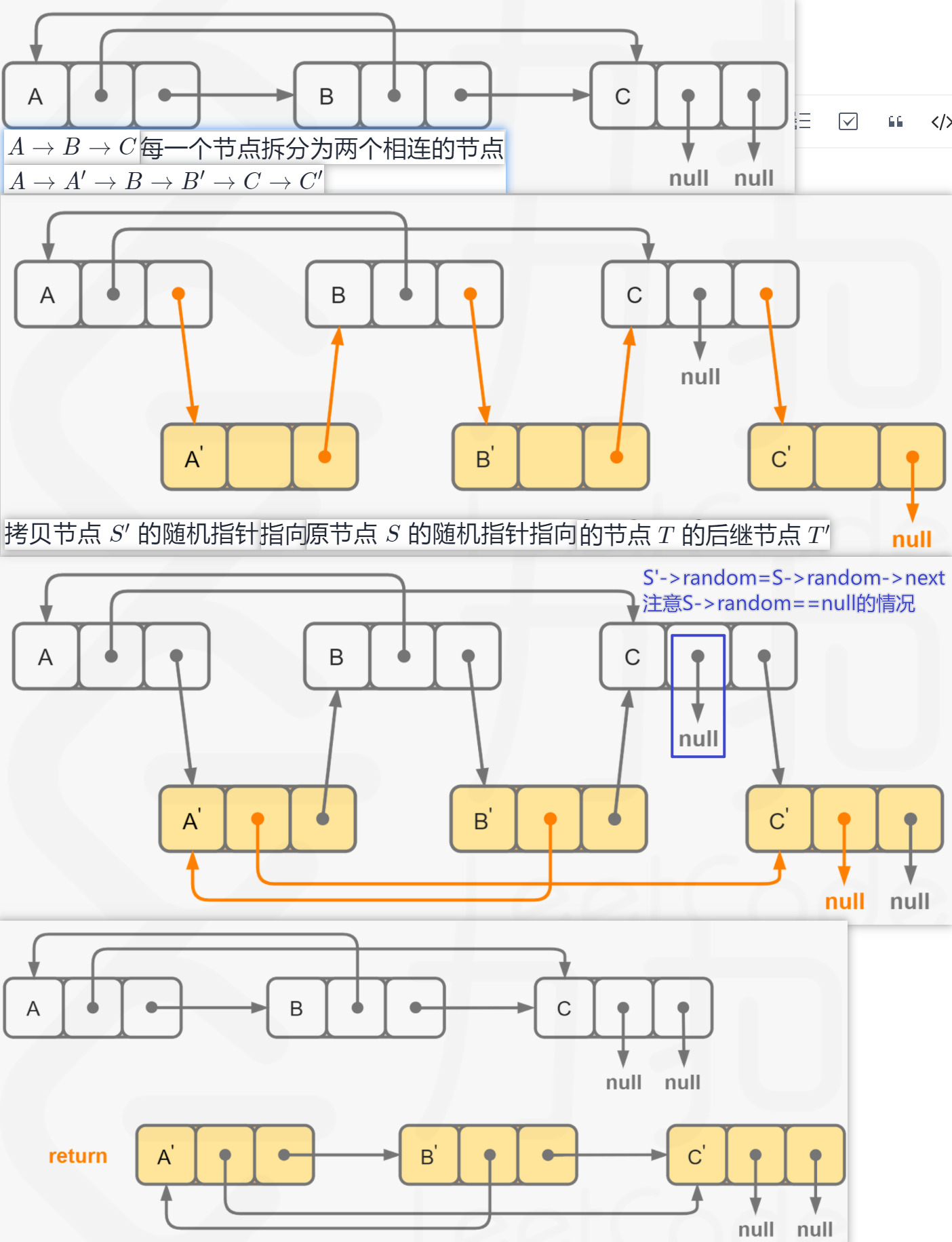
3.拼接+拆分
/* C++
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val; //自定义类的成员变量/(这里是数据成员)一般都加上前缀'_',这样可以避免数据成员与成员函数的参数同名
next = NULL;
random = NULL;
}
};
*/
class Solution {
public:
/** 1.迭代+哈希
* TC:O(N) 链表长
* SC:O(N) 哈希表
*/
Node* copyRandomList(Node* head) {
if(!head) return NULL;
unordered_map<Node*, Node*> map;
for(auto p = head; p; p = p->next) { //复制节点 构建<原链表,新链表>的map映射
map[p] = new Node(p->val);
}
for(auto p = head; p; p = p->next) { //构建新链表的 next random 指向
map[p]->next = map[p->next]; //原节点的next指向节点对应的新节点
map[p]->random = map[p->random];
}
return map[head];
}
/** 2.回溯+哈希
* TC:O(N) 链表长
* SC:O(N) 哈希表
*/
unordered_map<Node*, Node*> map; //递归要在外面定义
Node* copyRandomList(Node* head) {
if(!head) return NULL;
if(!map.count(head)) { //递归时随机指向节点可能创建
auto p = new Node(head->val);
map[head] = p; //复制节点 构建<原链表,新链表>的map映射
p->next = copyRandomList(head->next); //递归创建还未创建的节点
p->random = copyRandomList(head->random);
}
return map[head];
}
/** 3.拼接+拆分
* TC:O(N) 遍历3次链表
* SC:O(1) 省去了Map的开销
*/
Node* copyRandomList(Node* head) {
if(!head) return NULL;
for(auto p = head; p; p = p->next->next) {
auto q = new Node(p->val);
q->next = p->next;
p->next = q;
}
for(auto p = head; p; p = p->next->next) {
auto q = p->next;
q->random = p->random ? p->random->next : NULL;
}
auto newHead = head->next;
for(auto p = head; p; p = p->next) {
auto q = p->next;
p->next = p->next->next;
q->next = q->next ? q->next->next : NULL;
}
return newHead;
}
};
/* Java
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
class Solution {
/** 1.迭代+哈希
* TC:O(N) 链表长
* SC:O(N) 哈希表
*/
public Node copyRandomList(Node head) {
// 思路
// Node dummy = new Node(-1), pre = dummy, p = head;
// while(p != null) {
// Node node = new Node(p.val);
// pre.next = node;
// // pre->random = ?;
// pre = pre.next;
// p = p.next;
// }
if(head == null) return head;
Map<Node, Node> map = new HashMap<>();
for(Node p = head; p != null; p = p.next) { //复制节点 构建<原链表,新链表>的map映射
map.put(p, new Node(p.val));
}
for(Node p = head; p != null; p = p.next) { //构建新链表的 next random 指向
map.get(p).next = map.get(p.next); //原节点的next指向节点对应的新节点
map.get(p).random = map.get(p.random);
}
return map.get(head);
}
/** 2.回溯+哈希
* TC:O(N) 链表长
* SC:O(N) 哈希表
*/
Map<Node, Node> map = new HashMap<>(); //递归要在外面定义
public Node copyRandomList(Node head) {
if (head == null) return null;
// Map<Node, Node> map = new HashMap<>(); //放在这里会发生stackOverflow异常
if (!map.containsKey(head)) { //递归时随机指向节点可能创建
Node p = new Node(head.val);
map.put(head, p); //复制节点 构建<原链表,新链表>的map映射
p.next = copyRandomList(head.next); //指向节点还未创建->递归创建
p.random = copyRandomList(head.random);
}
return map.get(head);
}
/** 3.拼接+拆分
* TC:O(N) 遍历3次链表
* SC:O(1) 省去了Map的开销
*/
public Node copyRandomList(Node head) {
if (head == null) return null;
for(Node p = head; p != null; p = p.next.next) {
Node q = new Node(p.val);
q.next = p.next;
p.next = q;
}
for(Node p = head; p != null; p = p.next.next) {
Node q = p.next;
q.random = (p.random == null) ? null : p.random.next;
}
Node newHead = head.next;
for(Node p = head; p != null; p = p.next) {
Node q = p.next;
p.next = p.next.next;
q.next = (q.next == null) ? null : q.next.next;
}
return newHead;
}
}
d4 查找算法 easy
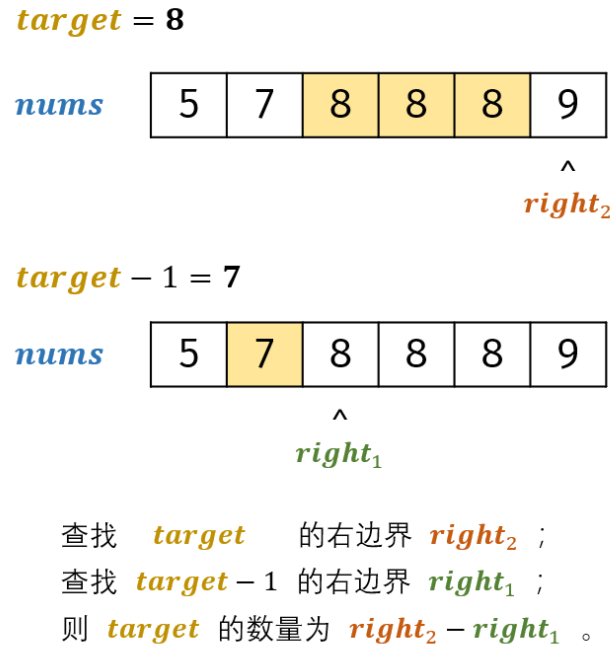
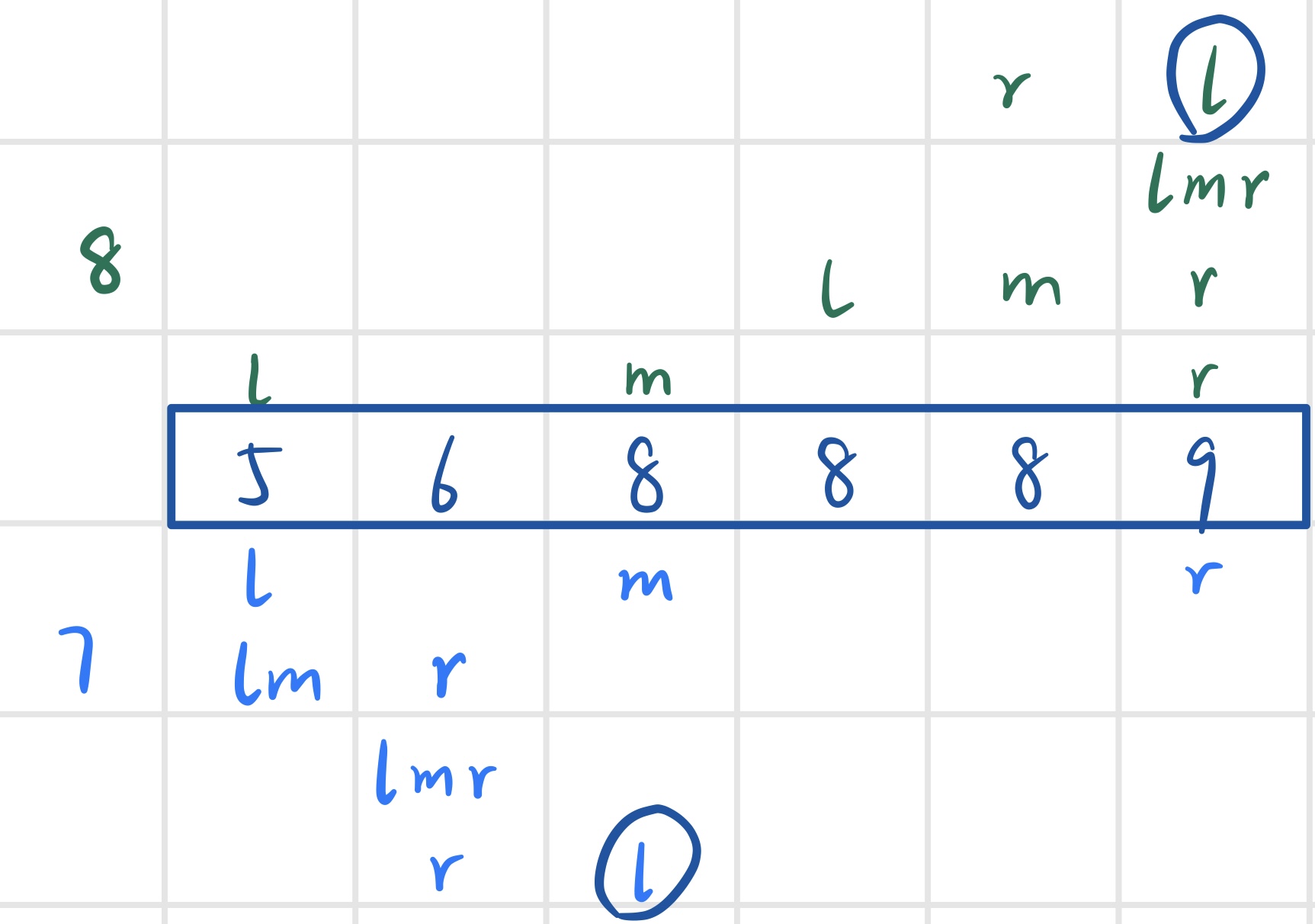
53 - I. 在排序数组中查找数字
难点:数字区间 找左右边界的两轮二分查找代码冗余-封装在一个binarySearch()里
//C++
/** 二分查找
* TC:O(logN)
* SC:O(1)
*/
int binarySearch(vector<int>& nums, int target) {
int l=0,r=nums.size()-1;
if(target<nums[l] || target>nums[r]) return -1; //减少重复循环
while(l<=r) {
int m=l+(r-l)/2;
if(target<nums[m]) r=m-1;
else if(target>nums[m]) l=m+1;
else return m;
}
return -1; //找不到
}
//C++
class Solution {
public int search(int[] nums, int target) {
return binarySearch(nums, target)-binarySearch(nums, target-1);
}
int binarySearch(vector<int>& nums, int target) {
int l=0,r=nums.size()-1;
while(l<=r) {
int m=l+(r-l)/2;
if(target>=nums[m]) l=m+1; //>= 右移 (<=则返回的l是左边界)
else r=m-1;
}
return l; //r<l 返回右边界
}
}
d5 查找算法 medium
4. 二维数组中的查找

//C++
class Solution {
public:
/**
* TC:O(M+N) M、N-矩阵行列数 最多循环M+N次
* SC:O(1)
*/
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
if(matrix.empty() || matrix[0].empty()) return false;
int l = matrix.size(), c = matrix[0].size(); //行l_i 列c_j !若数组空则matrix[0].size()空指针异常
//从右上角遍历 行下移 列左移
for(int i = 0, j = c - 1; i < l && j >= 0; ) { //max总步数l+c-2
if(target > matrix[i][j]) i++;
else if(target < matrix[i][j]) j--;
else return true;
}
return false;
}
};
//Java
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
int i = matrix.length - 1, j = 0; //数组为空(i=-1)不进入循环 则无需判空
//从左下角遍历 行i上移 列j右移
while(i >= 0 && j < matrix[0].length) {
if(target < matrix[i][j]) i--;
else if(target > matrix[i][j]) j++;
else return true;
}
return false;
}
}
11. 旋转数组的最小数字

//C++
class Solution {
public:
//O(N)暴力 遍历找到第一个比左边小的数
/**二分 未旋转数组所有元素>旋转数组最大元素
* TC:O(logN)
* SC:O(1)
*/
int minArray(vector<int>& numbers) {
int l=0, r=numbers.size()-1;
while(l<r) {
int m=l+(r-l)/2;
if(numbers[m]>numbers[r]) l=m+1;
else if(numbers[m]<numbers[r]) r=m;
else r--; //重复元素
}
return numbers[l]; //l=r时返回
}
};
50. 第一个只出现一次的字符
//C++
class Solution {
public:
/** 哈希表 <字符,是false否true重复>
* TC:O(N)
* SC:O(1) <-map字母表O(26)
*/
char firstUniqChar(string s) {
unordered_map<char, bool> m;
for(char c: s) {
m[c]=!m.count(c);
}
for(char c: s) {
if(m[c]) return c;
}
return ' ';
}
};
//Java
class Solution {
public char firstUniqChar(String s) { //最简便
Map<Character, Boolean> map = new HashMap<>();
for(char c: s.toCharArray()) {
map.put(c,!map.containsKey(c));
}
for(char c: s.toCharArray()) {
if(map.get(c)) return c;
}
return ' ';
}
//or
public char firstUniqChar(String s) {
Map<Character, Integer> map = new HashMap<>();
for(char c: s.toCharArray()) {
if(map.containsKey(c)) map.put(c,-1);
else map.put(c,1);
// map.merge(c,1,Integer::sum);
}
// for(char c: map.keySet()) { //检查映射
// System.out.print(map.get(c));
// }
for(char c: s.toCharArray()) {
if(map.get(c)==1) return c;
}
return ' ';
}
}
Java Map.merge()
d6/7 搜索与回溯算法 easy
树
树的每个节点有一个值和一个包含所有子节点的列表
从图的观点看,树 - 拥有 N 个节点和 N-1 条边的有向无环图
二叉树
每个节点最多有两个子树 - 左子树(<根) 右子树(>根)
| 方法 | 解决问题 | 数据结构 |
|---|---|---|
| 深度优先搜索 递归/迭代 | 前 中 后序遍历 | 栈 |
| 广度优先搜索 | 层序遍历 | 队列 |
| 遍历 | 特点 |
|---|---|
| 前 | 先入右子才能先弹出左子 |
| 中 | 输出递增的有序序列 中缀表达式(要检查操作优先级) 代码难多记 |
| 后 | 删除节点按后序遍历 后缀表达式/逆波兰式(数字入栈-遇到操作符弹出栈顶2个元素-计算结果返回入栈) |
遍历树时一定要检查访问地址是否为空并进行相应处理!
递归
TC = 递归次数 * 每次递归的TC
把递归抽象出一颗二叉树->递归树节点个数=递归次数
一棵深度(按根节点深度为1)为k的满二叉树节点个数= 2^k - 1
SC = 递归深度 * 每次递归的SC
定义
// C++
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
// Java
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
深度优先搜索_递归 TC:O(2^N) SC:O(N)?
// C++
vector<int> preorderTraversal(TreeNode* root) {
vector<int> v;
recur(root, v);
return v;
}
void recur(TreeNode* root, vector<int>& v) { //不加&会返回空结果 不加&-传值:修改形参不影响实参 加&-传址:修改形参也修改实参
if(!root) return;
v.push_back(root->val); //前序遍历 preorderTraversal
recur(root->left, v);
// v.push_back(root->val); //中序遍历 inorderTraversal
recur(root->right, v);
// v.push_back(root->val); //后序遍历
}
// Java
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
recur(root, list);
return list;
}
public void recur(TreeNode root, List<Integer> list) {
if(root == null) return;
list.add(root.val) //前序遍历
recur(root.left, list);
// list.add(root.val) //中序遍历
recur(root.right, list);
// list.add(root.val) //后序遍历
}
深度优先搜索_迭代 栈 TC:O(N) SC:O(N)?
- 前序遍历
// C++
vector<int> preorderTraversal(TreeNode* root) {
vector<int> v;
if(!root) return v;
stack<TreeNode*> s;
s.push(root);
while(!s.empty()) { //出根入右左
auto p = s.top();
s.pop();
v.push_back(p->val);
if(p->right) s.push(p->right); //右子先入栈 后出栈
if(p->left) s.push(p->left);
}
return v;
}
// Java
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root == null) return list;
Deque<TreeNode> stack = new LinkedList<>();
// Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while(!stack.isEmpty()) {
TreeNode node = stack.pop();
list.add(node.val);
if(node.right != null) stack.push(node.right);
if(node.left != null) stack.push(node.left);
}
return list;
}
- 中序遍历
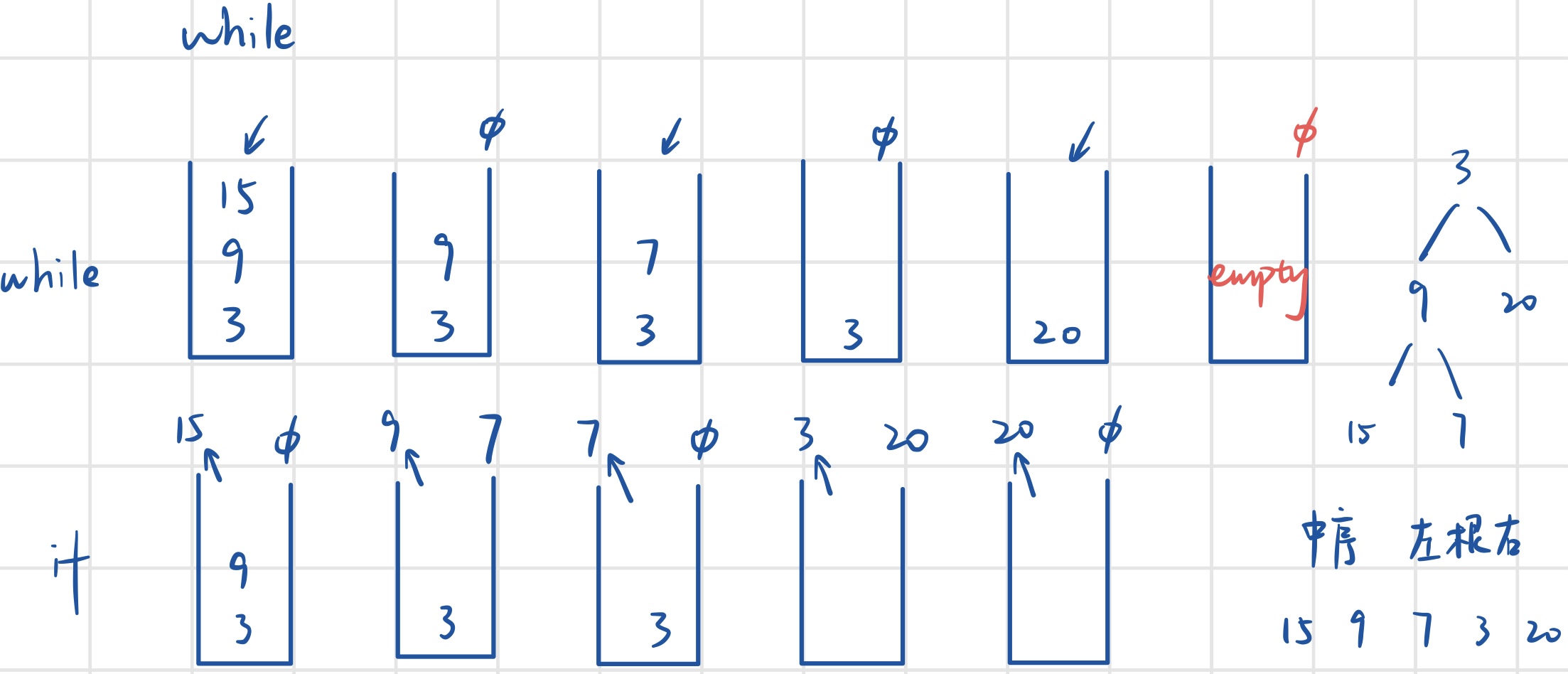
// C++
vector<int> inorderTraversal(TreeNode* root) {
vector<int> v;
if(!root) return v;
stack<TreeNode*> s;
while(root || !s.empty()) {
while(root) {
s.push(root);
root = root->left;
}
if(!s.empty()) {
root = s.top();
s.pop();
v.push_back(root->val);
root = root->right;
}
}
return v;
}
// Java
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer>list = new ArrayList<>();
if(root == null) return list;
Deque<TreeNode> stack = new LinkedList<>();
while(root != null || !stack.isEmpty()) {
while(root != null) {
stack.push(root);
root = root.left;
}
if(!stack.isEmpty()) {
root = stack.pop();
list.add(root.val);
root = root.right;
}
}
return l;
}
- 后序遍历
广度优先搜索(层序遍历) 队列
// C++
// 总共打印一行
vector<int> levelOrder(TreeNode* root) {
vector<int> v;
if(!root) return v;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()) { //出根入左右
auto p = q.front();
v.push_back(p->val);
q.pop();
if(p->left) q.push(p->left);
if(p->right) q.push(p->right);
}
return v;
}
// 每层打印一行
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
if(!root) return vv; //return {};
queue<TreeNode*> q;
q.push(root);
while(!q.empty()) {
//存放同一层结点
vector<int> v;
int n = q.size();
while(n--) {
auto p = q.front();
v.push_back(p->val);
q.pop();
if(p->left) q.push(p->left);
if(p->right) q.push(p->right);
}
vv.push_back(v);
}
return vv;
}
//之字形打印
// Java
public int[] levelOrder(TreeNode root) {
if(root == null) return new int[0];
List<Integer> v = new ArrayList<>();
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while(!q.isEmpty()) {
TreeNode p = q.poll(); //poll()返回队首并删除
v.add(p.val);
if(p.left != null) q.offer(p.left);
if(p.right != null) q.offer(p.right);
}
// return v.toArray(); //error: Object[] cannot be converted to int[] reason: 不带参数的toArray()返回的是Object[],使用时需要逐个元素强制类型转换
// Integer[] a = v.toArray(new Integer[v.size()]); //...
int[] a = new int[v.size()];
for(int i=0; i<a.length; i++) a[i] = v.get(i);
return a;
}
//每层打印一行
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ll=new ArrayList<>();
if(root==null) return ll;
Queue<TreeNode> q=new LinkedList<>();
q.offer(root);
while(!q.isEmpty()) {
//存放同一层结点
int n=q.size();
List<Integer> l=new ArrayList<>();
while(n-->0) {
TreeNode node=q.poll();
l.add(node.val);
if(node.left!=null) q.offer(node.left);
if(node.right!=null) q.offer(node.right);
}
ll.add(l);
//若此后l.clear()也会将ll中加入的l清空->ll.add(new ArrayList<>(l))这样就不会了
}
return ll;
}
//之字形打印
26. 树的子结构
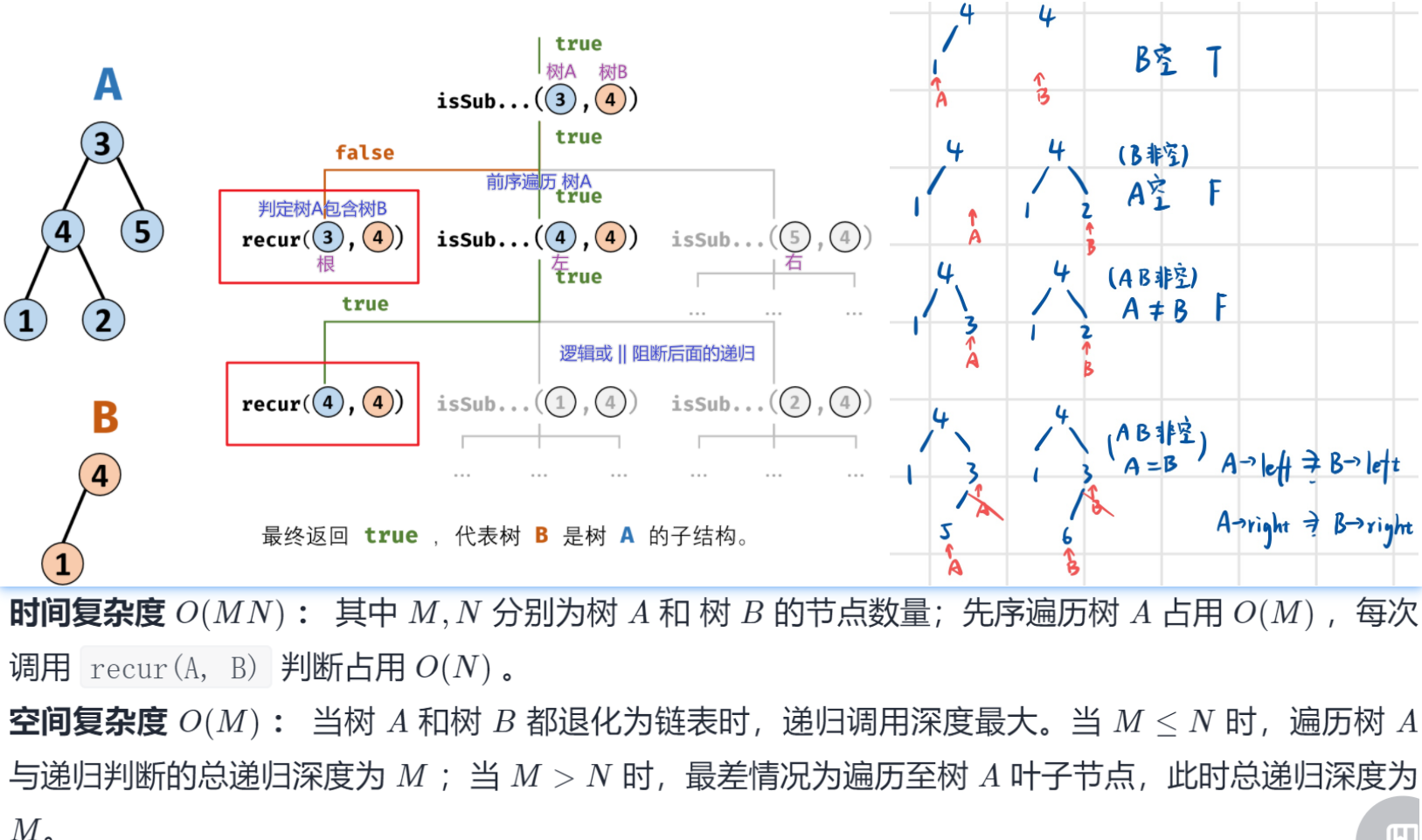 solution
solution
// C++
class Solution {
public:
//TC:O(MN) SC:O(M) M,N(设M>N)--A,B节点数
bool isSubStructure(TreeNode* A, TreeNode* B) {
// if(A==NULL || B==NULL) return false;
// return isSub(A,B) || isSubStructure(A->left,B) || isSubStructure(A->right,B);
//前序遍历 在A中找B根 (B是否A的子结构 || B是否A左子的子结构 || B是否A右子的子结构)
return (A!=NULL && B!=NULL) && (recur(A,B) || isSubStructure(A->left,B) || isSubStructure(A->right,B));
}
//包含判断
bool recur(TreeNode* A, TreeNode* B) {
if(B==NULL) return true; //B空->匹配完
if(A==NULL || A->val!=B->val) return false; //B非空 A空/AB不等->不匹配
return recur(A->left,B->left) && recur(A->right,B->right); //AB非空 AB等->继续判断左右子树(直到B空->匹配完) A左右子树都包含B左右子树才算A树包含B树
}
};
// Java
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
return (A != null && B != null) && (recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B));
}
public boolean recur(TreeNode A, TreeNode B) {
if(B == null) return true;
if(A == null || A.val != B.val) return false;
return recur(A.left, B.left) && recur(A.right, B.right);
}
}
28. 对称的二叉树
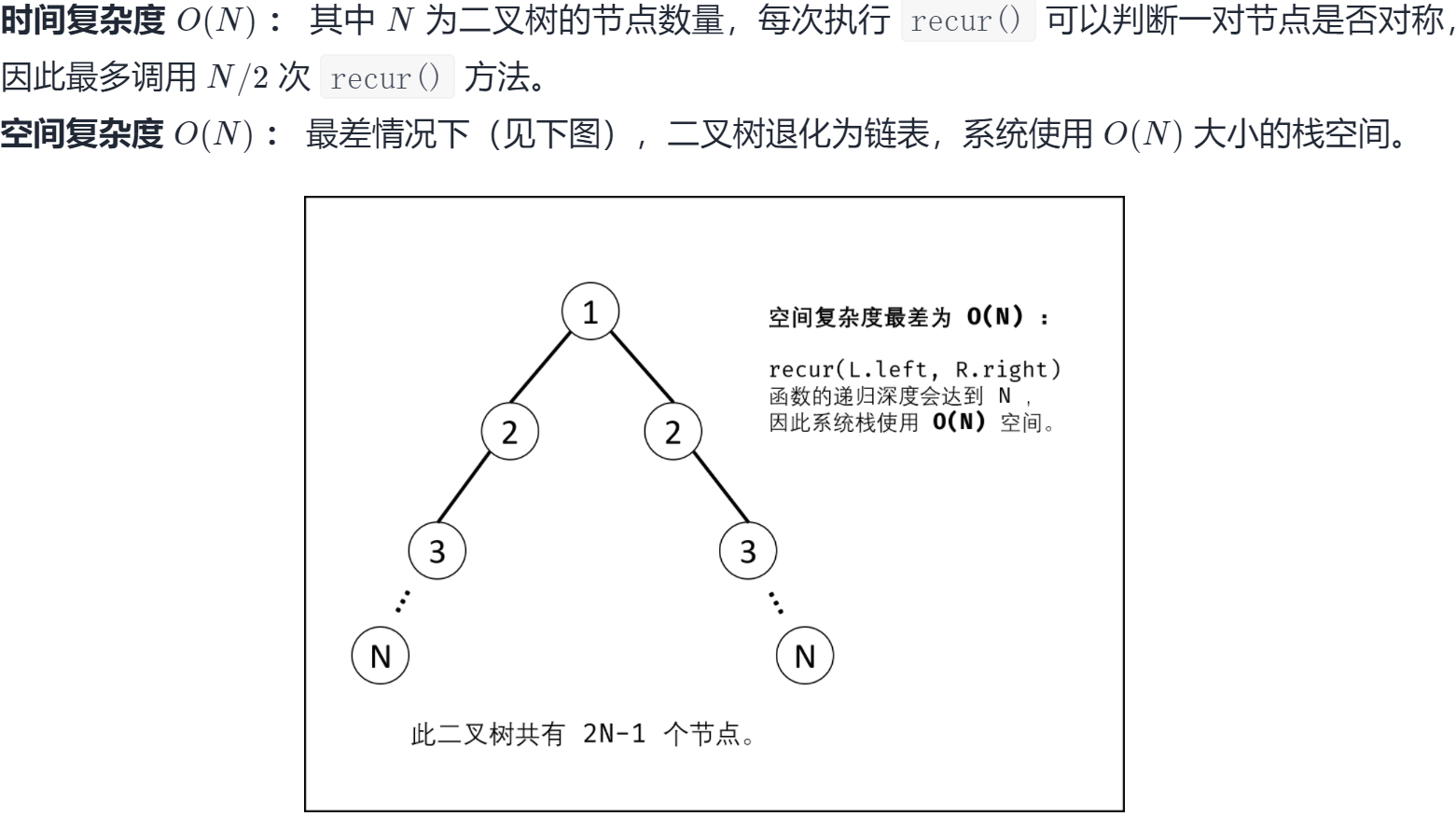
// C++
class Solution {
public:
// 1.二叉树与其镜像相等->对称
bool isSymmetric(TreeNode* root) {
return isSameTree(root, mirrorTree(root)); //可以进入方法再判空
}
/** 问题:直接用root翻转成对称树与原树比较会始终返回true
* 原因:改变了原二叉树结构,比较时始终传入相同的两棵树
* 解决:翻转时创建新树,而不是原地修改旧树
*/
TreeNode* mirrorTree(TreeNode* root) {
if(root==NULL) return NULL;
// auto t=root->left;
// root->left=mirrorTree(root->right);
// root->right=mirrorTree(t);
// return root;
// 创建新树!
auto newRoot = new TreeNode(root->val);
auto t=root->left;
newRoot->left=mirrorTree(root->right);
newRoot->right=mirrorTree(t);
return newRoot;
}
bool isSameTree(TreeNode* A, TreeNode* B) {
if(A==NULL && B==NULL) return true;
if(A==NULL || B==NULL || A->val != B->val) return false;
return isSameTree(A->left,B->left) && isSameTree(A->right,B->right);
}
// 2.判断左右子树是否对称
bool isSymmetric(TreeNode* root) { //访问root的left/right/val前要先判空
return root==NULL ? true : recur(root->left,root->right);
}
bool recur(TreeNode* L, TreeNode* R) {
// 对称的节点相等
if(L==NULL && R==NULL) return true;
if(L==NULL || R==NULL || L->val != R->val) return false;
return recur(L->left,R->right) && recur(L->right,R->left);
}
};
d8 动态规划 Dynamic Programming (DP) easy
有重叠子问题
每个状态由上个状态推导(区分于贪心-局部最优选)
步骤:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式(状态转移方程) ->决定3
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
debug: 打印dp数组日志
和推导一样->递归公式、初始化、遍历顺序有bug
不一样->代码实现细节有bug
Fibonacci
/*
* @lc app=leetcode.cn id=509 lang=cpp
*
* [509] 斐波那契数
*/
#include <bits/stdc++.h>
using namespace std;
// @lc code=start
class Solution {
public:
/**
* @brief 递归
* TC = 递归次数(递归树节点个数) * 每次递归的TC = O(2^N)
* SC = 递归深度 * 每次递归的SC = O(N)
* 题目有时间限制会TimeOut->答案需要取模1e9+7(1000000007),如计算初始结果为:1000000008,请返回1
*/
int fib(int n) {
return n < 2 ? n : (fib(n - 1) + fib(n - 2)) % 1000000007; //每次递归的TC=O(1)
}
// TC:O(N) SC:O(N) 动态规划-dp数组
int fib(int n) {
if (n < 2) return n;
// vector<int> dp(n+1,0); //只初始化2个,就不全初始化为0
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
}
return dp[n];
}
// TC:O(N) SC:O(1) 细节优化(状态压缩-缩小DPtable的大小)
int fib(int n) {
if (n < 2) return n;
int a = 0, b = 1, c;
for (int i = 2; i <= n; i++) {
c = (a + b) % 1000000007;
a = b;
b = c;
}
return c;
}
};
// @lc code=end
int main() {
int n;
cin >> n;
Solution s;
cout << s.fib(n) << endl;
return 0;
}
import java.util.Scanner;
//Java:斐波那契数
public class P509_FibonacciNumber {
public static void main(String[] args) {
Solution solution = new P509_FibonacciNumber().new Solution();
// TO TEST
Scanner in = new Scanner(System.in);
int n = in.nextInt();
System.out.println(solution.fib(n));
}
class Solution {
/**
* 递归
* TC = 递归次数(递归树节点个数) * 每次递归的TC = O(2^N)
* SC = 递归深度 * 每次递归的SC = O(N)
* 题目有时间限制会TimeOut->答案需要取模1e9+7(1000000007),如计算初始结果为:1000000008,请返回1
* @param n
* @return
*/
public int fib(int n) {
return n < 2 ? n : (fib(n - 1) + fib(n - 2)) % 1000000007; //每次递归的TC=O(1)
}
//TC:O(N) SC:O(N) 动态规划-dp数组
public int fib(int n) {
if (n < 2) return n;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
}
return dp[n];
}
// TC:O(N) SC:O(1) 动态规划-dp数组优化
public int fib(int n) {
if (n < 2) return n;
int a = 0, b = 1, c = 0; //Java c=0要先初始化后面才能赋值
for (int i = 2; i <= n; i++) {
c = (a + b) % 1000000007;
a = b;
b = c;
}
return c;
}
}
}
10- II. 青蛙跳台阶问题
台阶数,跳法数:0,1 / 1,1 / 2,2 / 3,3 / 4,5 / 5,8 -> Fibonacci
注:若题目给定n是正整数 就不应该初始化dp[0],则i从3开始递推
63. 股票的最大利润
// C++
class Solution {
public:
//贪心
int maxProfit(vector<int>& prices) {
int minPrice=INT_MAX, maxPro=0;
for(int i=0; i<prices.size(); i++) {
minPrice=min(minPrice, prices[i]); //是前些天还是当天价格更低
maxPro=max(maxPro, prices[i]-minPrice); //是前些天还是当天卖出的最大利润更大
}
return maxPro;
}
};
// Java
class Solution {
//贪心
public int maxProfit(int[] prices) {
int minPrice=Integer.MAX_VALUE, maxPro=0;
for(int i=0;i<prices.length;i++) {
minPrice=Math.min(minPrice, prices[i]);
maxPro=Math.max(maxPro, prices[i]-minPrice);
}
return maxPro;
}
}
d9 DP medium
42. 连续子数组的最大和

// C++
class Solution {
public:
// TC:O(N) SC:O(1)
int maxSubArray(vector<int>& nums) {
int sum=nums[0];
for(int i=1; i<nums.size(); i++) {
nums[i]+=max(nums[i-1], 0);
sum=max(sum, nums[i]);
}
return sum;
}
};
d10 DP medium
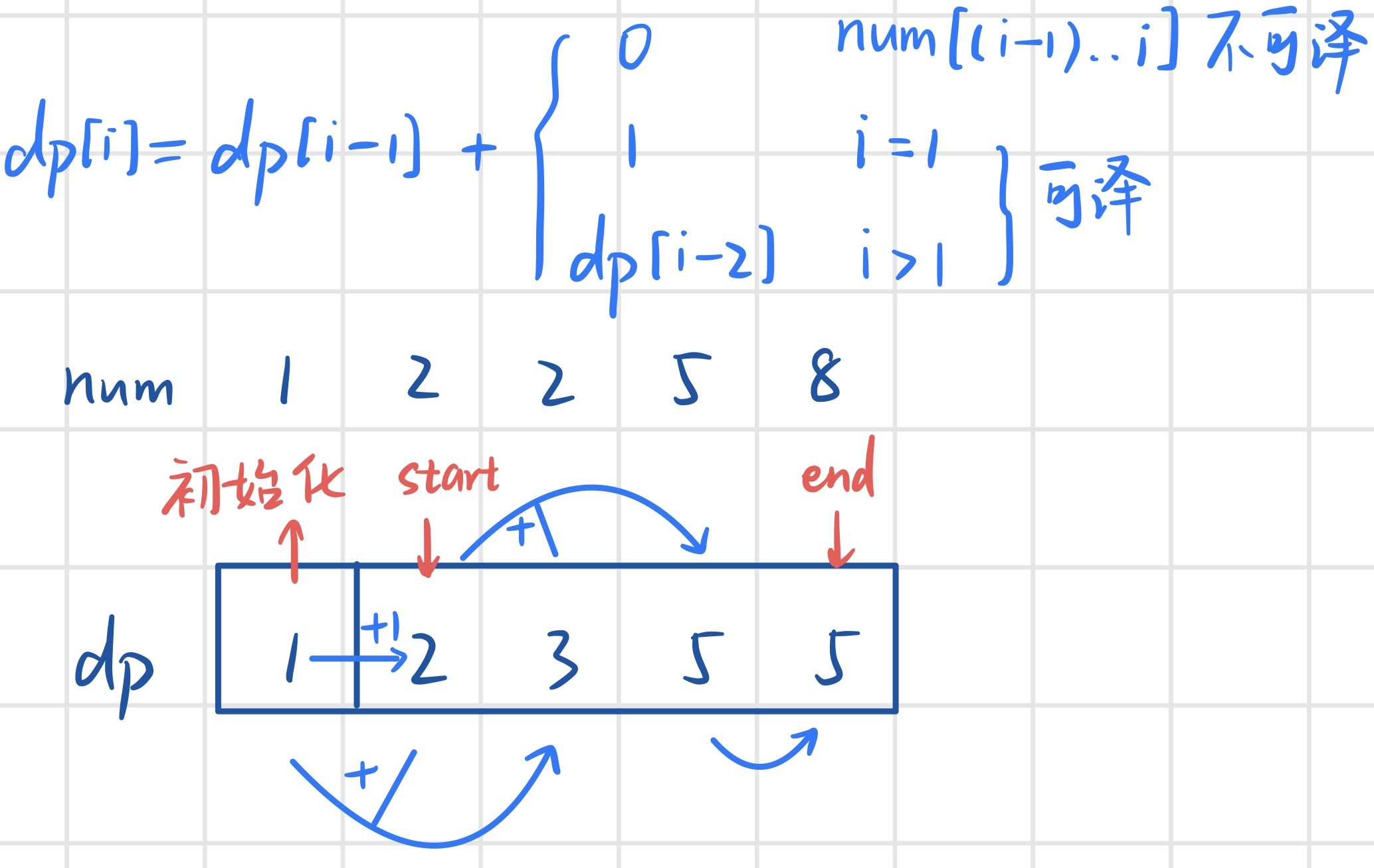
46. 把数字翻译成字符串
结果只要求总数,不要求具体的计算过程-> dp:自底向上->小问题-递推-结果
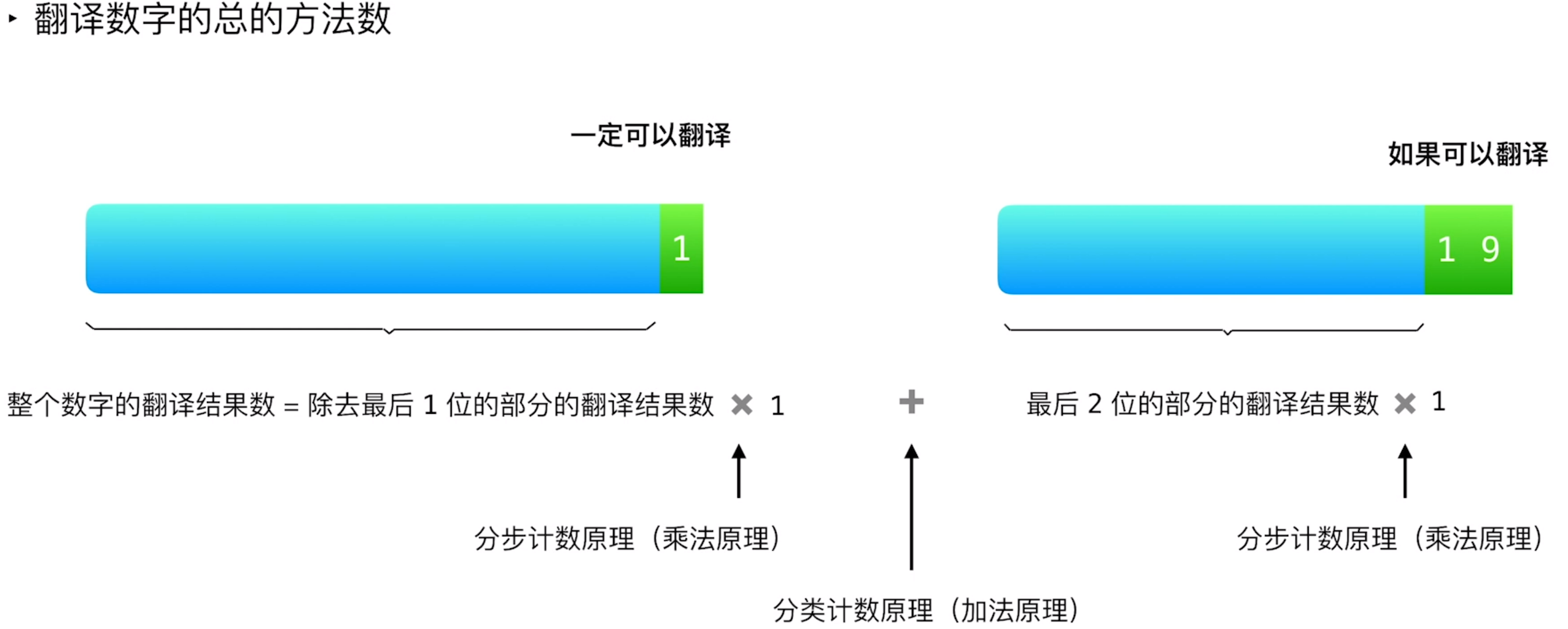

// Java
class Solution {
/** dp[i]:前i个数的翻法 dp[0]=1 dp[i]=dp[i-1]+(>9&&<26->dp[i-2] / i=1->1)
* TC:O(N)
* SC:O(N)
*/
public int translateNum(int num) {
// String s = num + ""; //Java不建议这样写.测试慢
String s = String.valueOf(num);
int n = s.length();
if(n < 2) return n;
int[] dp = new int[n];
dp[0] = 1;
// char[] c = s.toCharArray();
for(int i = 1; i < n; i++) {
// s[(i-1)..i]<26 没考虑>9 0开头也不可译! 注意考虑i=1的情况->dp[i-2]越界
int x = Integer.valueOf(s.substring(i - 1, i + 1));
// int x = 10 * (c[i-1] - '0') + (c[i] - '0');
dp[i] = dp[i-1];
if(x > 9 && x < 26) dp[i] += (i == 1) ? 1 : dp[i-2];
}
return dp[n-1];
}
// dp空间优化 SC:O(1)
public int translateNum(int num) {
String s = String.valueOf(num);
int n = s.length();
if(n < 2) return n;
int a = 0, b = 1, c = 0; //Java c=0要先初始化后面才能赋值
for(int i = 1; i < n; i++) {
int x = Integer.valueOf(s.substring(i - 1, i + 1));
c = b;
if(x > 9 && x < 26) c += (i == 1) ? 1 : a;
a = b;
b = c;
}
return c;
}
}
其它写法


48. 最长不含重复字符的子字符串
d11 双指针 easy
18. 删除链表的节点
说明:题目保证链表中节点的值互不相同,若使用 C 或 C++ 语言,无需 free 或 delete 被删除的节点
// Java
class Solution {
/**头结点特殊情况:单独处理->双指针 虚拟头->单指针
* TC:O(N)
* SC:O(1)
*/
public ListNode deleteNode(ListNode head, int val) {
if(head==null) return null;
ListNode dummy=new ListNode(-1); // 虚拟头
dummy.next=head;
for(ListNode p=dummy; p.next!=null; p=p.next) {
if(p.next.val==val) {
p.next=p.next.next;
break; // <-链表节点值唯一 可直接break
}
}
return dummy.next;
}
}
若链表节点有重复值
22. 链表中倒数第k个节点
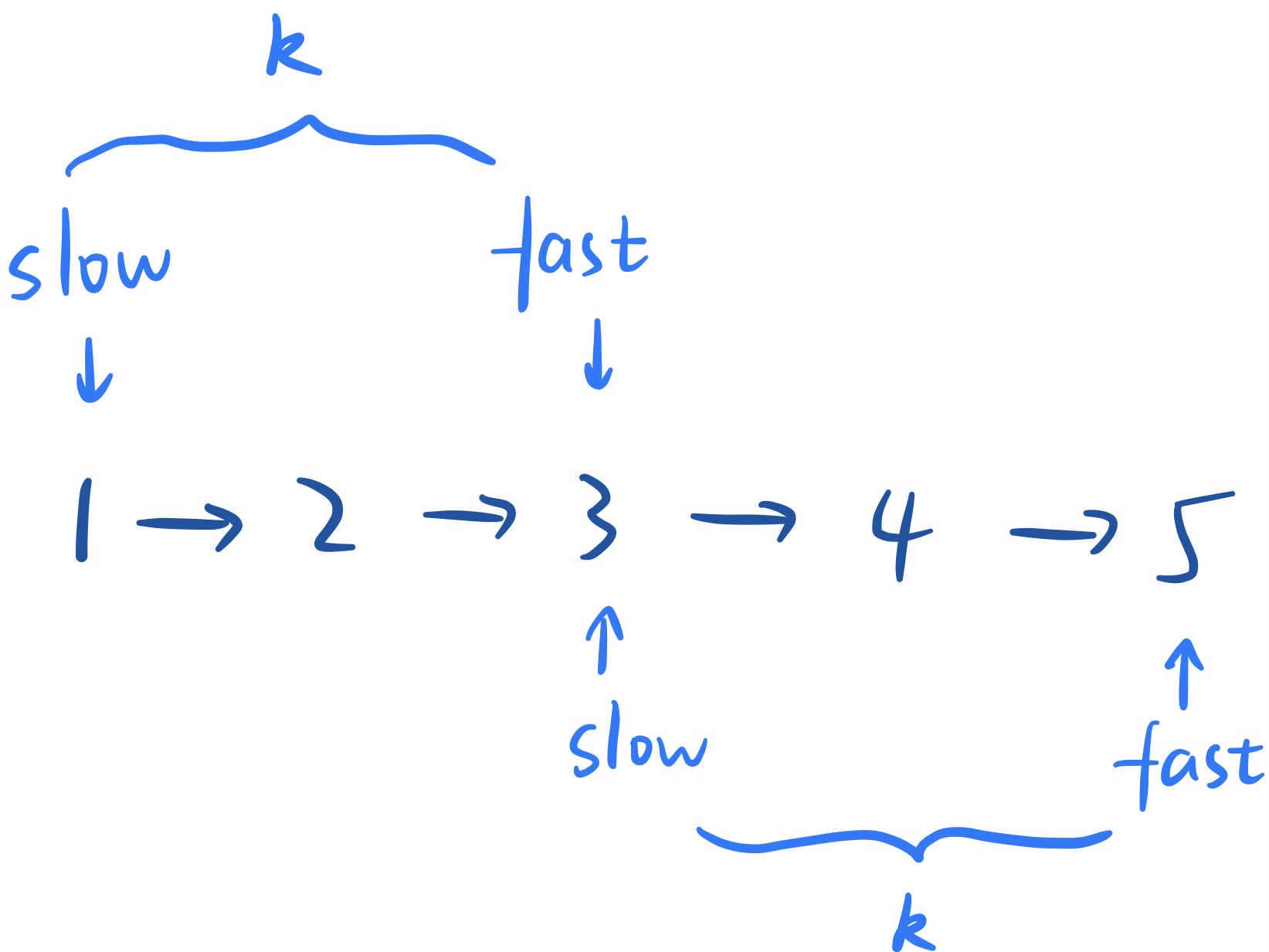
// Java
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
if(head==null) return null;
ListNode slow=head, fast=head;
while(k>1) {
fast=fast.next;
k--;
}
while(fast.next!=null) {
slow=slow.next;
fast=fast.next;
}
return slow;
}
}
删除链表的倒数第N个节点
d21 位运算 easy
56 - I. 数组中数字出现的次数
Java 中无符号右移为 >>>
无符号右移(>>>)跟右移(>>)不同
对于正数,>>>不会变成负数(相当于/2取整)
对于负数,>>>会将负数变成正数
在C++中实现无符号右移,可以先将拟进行无符号右移的数转换成无符号类型,然后执行普通右移
unsigned int a;
unsigned int b=a>>whatever;
// Java
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int ans=0;
n^=0;
while(n!=0) {
ans+=n&1;
n>>>=1;
}
return ans;
}
}
65. 不用加减乘除做加法
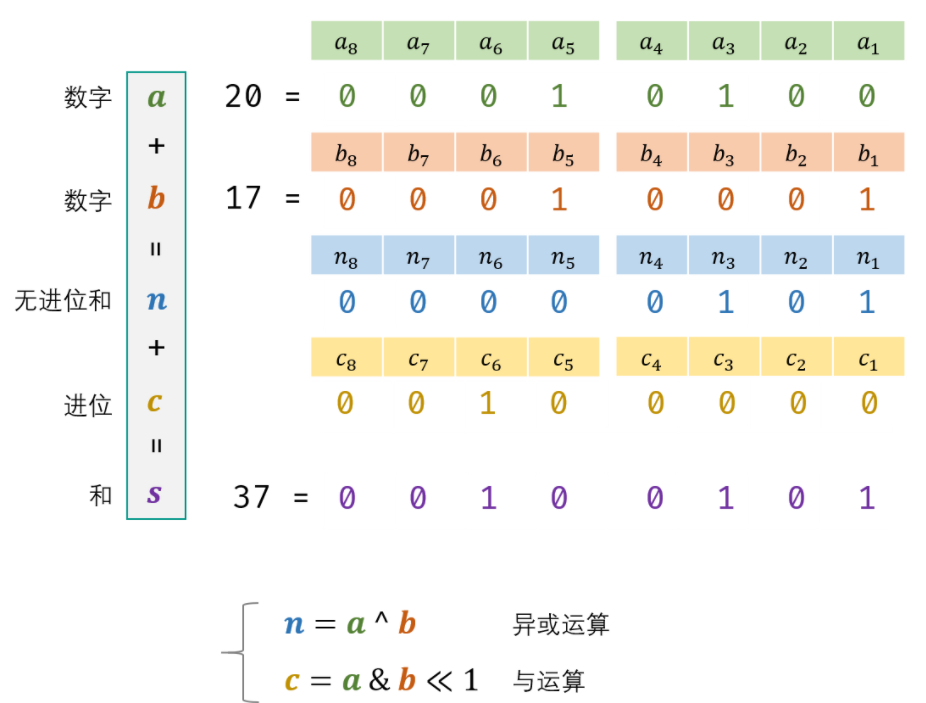
// Java
class Solution {
// 无进位和n=a^b 进位c=a&b<<1 和s=n+c(不能出现+->重复前面a+b的方法直到c=0)
public int add(int a, int b) {
while(b!=0) {
int c = (a&b) << 1; // <<优先级高于&
a ^= b;
b = c;
}
return a;
}
}
d22 位运算 medium
最后
以上就是冷艳学姐最近收集整理的关于剑指offer的全部内容,更多相关剑指offer内容请搜索靠谱客的其他文章。








发表评论 取消回复