青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
（答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1）

示例 1：

输入：n = 2
输出：2
示例 2：

输入：n = 7
输出：21
示例 3：

输入：n = 0
输出：1

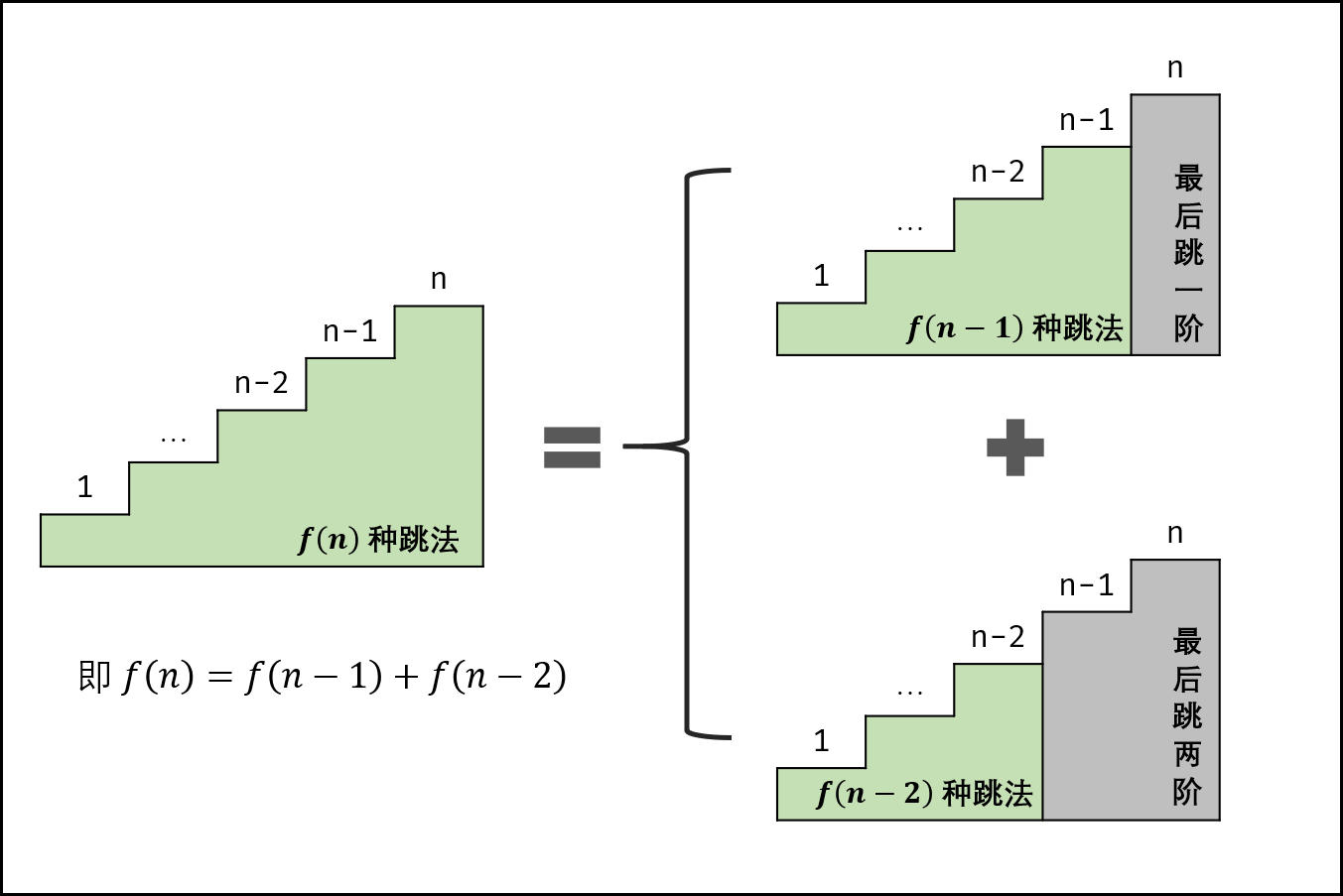
设跳上 n 级台阶有 f(n)f(n) 种跳法。在所有跳法中，青蛙的最后一步只有两种情况： 跳上 1 级或 2 级台阶。
当为 1 级台阶： 剩 n−1 个台阶，此情况共有 f(n-1)f(n−1) 种跳法；
当为 2 级台阶： 剩 n−2 个台阶，此情况共有 f(n-2)f(n−2) 种跳法。
f(n)f(n) 为以上两种情况之和，即 f(n)=f(n-1)+f(n-2)f(n)=f(n−1)+f(n−2) ，以上递推性质为斐波那契数列。本题可转化为 求斐波
青蛙跳台阶问题： f(0)=1 , f(1)=1 , f(2)=2 ；
斐波那契数列问题： f(0)=0 , f(1)=1 , f(2)=1 。

动态规划解析：

状态定义： 设 dp 为一维数组，其中 dp[i] 的值代表 斐波那契数列第 $i$ 个数字 。
转移方程： dp[i + 1] = dp[i] + dp[i - 1] ，即对应数列定义 f(n + 1) = f(n) + f(n - 1)；
初始状态： dp[0] = 1, dp[1] = 1 ，即初始化前两个数字；
返回值： dp[n] ，即斐波那契数列的第 n 个数字。

代码如下：

public class FrogJumpingSteps {
    public static void main(String[] args) {
        int num = numWays(7);
        System.out.println(num);
    }

    /**
     * @param n: 输入的台阶数
     * @return: 返回方法数
     */
    public static int  numWays(int n){
        if(n == 0){
            return 1;
        }

        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for(int i = 2; i < n+1; i++){  //上面不进行判断n == 1的原因是，如果n = 1,不能够执行循环里面内容，而且dp[1]已经进行了赋值
            dp[i] = (dp[i-1]+dp[i-2]) % 1000000007;
        }
        return dp[n];
    }
}

最后

以上就是漂亮饼干为你收集整理的青蛙跳台阶问题的全部内容，希望文章能够帮你解决青蛙跳台阶问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。