枚举:枚举的算法核心是列出所有可能的答案种类,并且逐个尝试,直到找到答案为止,但在实际操作中,我们往往不会直接将所有的数据直接进行判断,而是通过设计,把一些显而易见不是答案的数据排除掉,这是枚举在使用时的核心。
例题:
那么我们在设计这道题的算法的时候,由于高峰都是在同一天,那么我们可以先找到所有的体力高峰的日期,这样就大大缩小判断的次数,从而使得枚举更加有效,代码如下:
#include <iostream>
#include <cstdio>
using namespace std;
#define MAX 21252
int main()
{
int d,p,e,i,caseNo=0;
while(scanf("%d%d%d%d",&p,&e,&i,&d)&&p!=-1)
{
++caseNo;
int k;
for(k=d+1;(k-p)%23;k++);//当循环结束的时候,记录下这个值,这个日期是体力高峰的日期
for(;(k-e)%28;k+=23);//同理继续尝试
for(;(k-i)%33;k+=23*28);
printf("Case%d:The next triple peak occurs in%d",caseNo,k-d);
}
return 0;
}


#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
//本题枚举的思想是,假设一枚是假币,然后测试数据,看是否符合预期
char Left[3][7];
char Right[3][7];
char Result[3][7];
bool IsFake(char c,bool light);//bool函数只会返回0和1,表示某件事的真与假。
//light这个参数表示这个硬币是轻质的,如果我们要假设他是硬质的,那么就应该要在后续做某些处理
//这里后续再说(bool的值传进去的是true或者是flase)如果传进去的是true ,那么就假设默认硬币是轻质的
int main()
{
int t,i;
scanf("%d",&t);
while(t--)//CASE读入的读法
{
for(i=0;i<3;i++)
{
cin>>Left[i]>>Right[i]>>Result[i];//逐步读入数据
}
for(char c='A';c<='L';c++)
{
if(IsFake(c,true))//轻的
{
printf("The coin %c is Fake and it is lightern",c);
break;
}
else if(IsFake(c,false))
{
printf("The coin %c is Fake and it is heaviern",c);
break;
}
}
}
return 0;
}
bool IsFake(char c,bool light)
{
for(int i=0;i<3;i++)
{
char *pleft,*pright;//以指针的方式来存储需要判断的左右两端的字符串
if(light)
{
pleft=Left[i];
pright=Right[i];
}
else//如果是重的,会发现其实只是对调了变量的位置,为了避免重新定义变量名,那么就可以直接将其对调,其后续结果是一致的
{
pleft=Right[i];
pright=Left[i];
}
switch(Result[i][0])//这里用来判定天平右侧的情况,来帮助我们测试数据的正确与否
{
case 'u':
if(strchr(pright,c)==NULL)
{
return false;
}
break;
case 'e':
if(strchr(pright,c)||strchr(pleft,c))
{
return false;
}
break;
case 'd':
if(strchr(pleft,c)==NULL)
{
return false;
}
break;
//up的情况,此处仍然是以轻质为前提进行编写的,那么就是假币存在右边
}
}
return true;
}
熄灯问题:
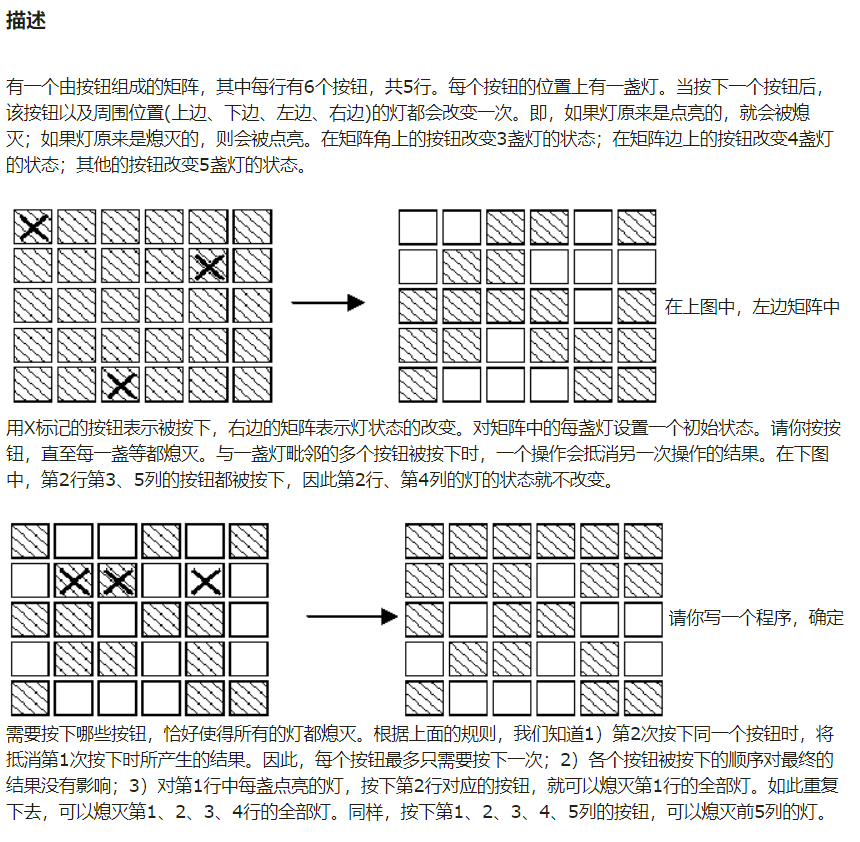
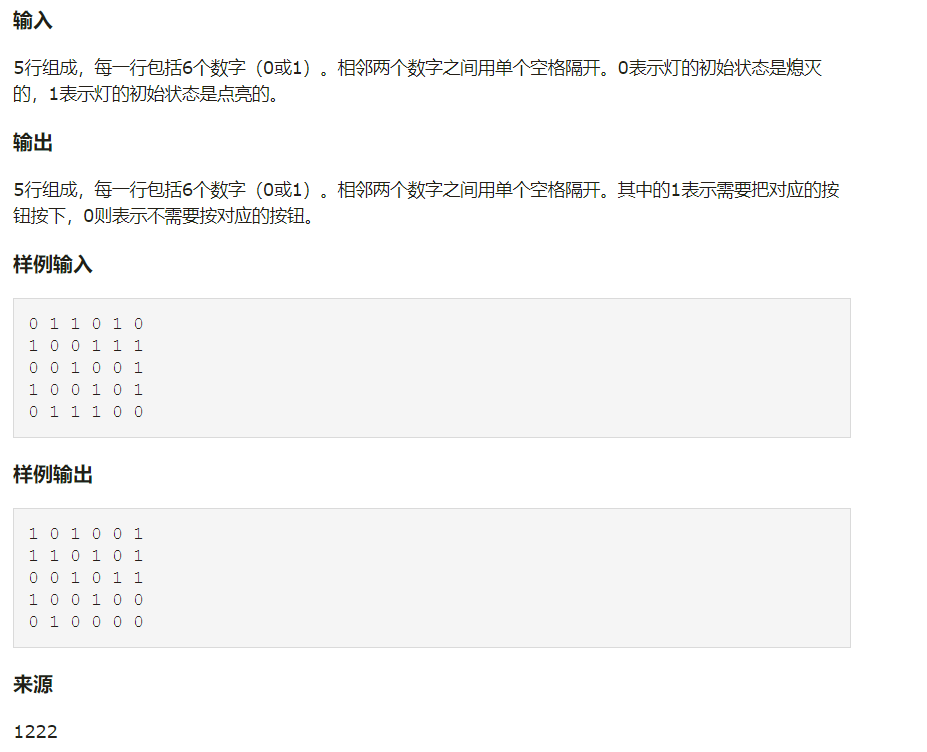
//要求是要给定矩阵中每盏灯的初始状态,求一种按钮方案,使得所有的灯都熄灭
//熄灯问题,如果是在中间位置,那么最多将会影响五盏灯
//在矩阵角上的的按钮被按下,将会改变三盏灯的状态
//在边上的按钮被按下,将会改变四盏灯的状态
//思考:一个开关,按几次,是有意义的?(第二次按下同一个开关的时候,将会抵消掉第一次按下开关的效果)
//对按钮的次序没有限制,找到那一种方案即可
/与一盏灯毗邻的多个按钮被按下的时候,一个操作会抵消另一次操作的结果/
//基本思路是:如果能够找到某个局部,使得这个局部被确定制定,剩下的状态是确定的,或者是不多的n种,只需要枚举剩下的情况
//来确定是否满足条件即可,那么我们只需要枚举这个局部的状态即可
//那么将这个思想转化为题目上来,就是说,我们在确定了第一行的状态之后,如果要使得第一行的灯全部熄灭,
//那么只能对第二行的灯进行操作,使得第一行的灯全部关闭,而这又恰恰确定了第二行的操作方案
//而这又引起了第三行的确定…直到最后一行,熄灯操作结束。
问题三:口口口+口口口=口口口,将数字1-9分别填入9个口中,每个数字只能使用一次使得等式成立,例如173+286=459就是一种成立的式子,但是我们需要注意286+173=459,这是同一种组合
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <ctype.h>
//根据枚举思想,我们只需要枚举每一位上所有的可能就可以了,但是判断带来的代码量和计算量可能导致超时
//所以需要优化这种暴力的枚举思路
//使用标记法(创建一个book数组来解决互不相等的问题)
int main()
{
int a[10]={0},i,count=0,book[10],sum;
for(a[1]=1;a[1]<=9;a[1]++)
for(a[2]=1;a[2]<=9;a[2]++)
for(a[3]=1;a[3]<=9;a[3]++)
for(a[4]=1;a[4]<=9;a[4]++)
for(a[5]=1;a[5]<=9;a[5]++)
for(a[6]=1;a[6]<=9;a[6]++)
for(a[7]=1;a[7]<=9;a[7]++)
for(a[8]=1;a[8]<=9;a[8]++)
for(a[9]=1;a[9]<=9;a[9]++)
{
for(i=1;i<=9;i++)
{
book[i]=0;
}
for(i=1;i<=9;i++)
{
book[a[i]]=1;//只有a[i]不同数了才会使得book里面的元素变化所以可以标记
}
sum=0;
for(i=1;i<=9;i++)
{
sum+=book[i];
}
if(sum==9&&a[1]*100+a[2]*10+a[3]+a[4]*100+a[5]*10+a[6]==a[7]*100+a[8]*10+a[9])
{
count++;
printf("%d%d%d+%d%d%d=%d%d%dn",a[1],a[2],a[3],a[4],a[5],a[6],a[7],a[8],a[9]);
}
}
printf("count=%d",count/2);
return 0;
}
问题四:炸弹人问题.
我们将炸弹人的地图模型化,墙体用#表示,怪物用G表示,空地用.表示,炸弹的爆炸方向是上下左右四个方向A,最终计算出,如何放置炸弹可以消灭掉最多的怪物。
基本移动的模拟
while(a[x][y]!='#')
{
if(a[x][y]=='G')
{
sum++;//消灭掉一个贵物
}
x++;//向下走直到撞墙
}
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <ctype.h>
#define n 13
#define m 13
//如何来模拟出炸弹爆炸的方向呢?
//只需要搞清楚一个方向,其他的方向都是一样的,比如说向下就是y不变,而x++直到遇到墙为止
//那么那么归纳一下,向左:x不变y--,向右:x不变,y++,向上:y不变,x--,向下:y不变,x++
//可以表示为:
/*while(a[x][y]!='#')
{
if(a[x][y]=='G')
{
sum++;//消灭掉一个贵物
}
x++;//向下走直到撞墙
}
*/
int main()
{
char a [n][m] = {
{'#', '#', '#', '#', '#', '#', '#', '#', '#', '#'},
{'#', 'G', 'G', '.', 'G', 'G', 'G', '#', '.', '#'},
{'#', '#', '#', 'G', '#', '.', 'G', 'G', 'G', '#'},
{'#', '#', '.', '.', '#', 'G', '#', '#', '#', '#'},
{'#', '.', '#', 'G', '#', 'G', 'G', 'G', '.', '#'},
{'#', '.', '#', 'G', '.', '.', '#', '#', 'G', '#'},
{'#', '#', '.', 'G', 'G', 'G', 'G', '.', 'G', '#'},
{'#', 'G', '.', '#', '.', '#', '.', '.', '#', '#'},
{'#', '#', '#', '.', '#', '#', 'G', 'G', '.', '#'},
{'#', '#', '#', '#', '#', '#', '#', '#', '#', '#'}
};
int max=0,count=0,x,y,q,p,i,j;
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
{
if(a[i][j]=='.')
{
count=0;
x=i,y=j;
while(a[x][y]!='#')//向上爆炸
{
if(a[x][y]=='G')
{
count++;
}
x--;
}
x=i,y=j;
while(a[x][y]!='#')//向下爆炸
{
if(a[x][y]=='G')
{
count++;
}
x++;
}
x=i,y=j;
while(a[x][y]!='#')//向左爆炸
{
if(a[x][y]=='G')
{
count++;
}
y--;
}
x=i,y=j;
while(a[x][y]!='#')//向右爆炸
{
if(a[x][y]=='G')
{
count++;
}
y++;
}
if(max<count)
{
max=count;
p=i;
q=j;
}
}
}
}
printf("将炸弹放在第%d行第%d列的时候将会消灭掉%d个怪物,是最多的。n",p,q,max);
return 0;
}
问题五:火柴棍等式
已知有n根火柴棍,希望拼出形如A+B=C的式子,ABC均是用火柴棍拼出来的整数,若该数非0,那么最高位就不能是0。求问有n根的情况下,能够拼出几个式子。(n<=24)
注意:1.加号与等号各自需要两根火柴棍。
2.如果A不等于B,那么A+B=C和B+A=C可以被视作两个不同的式子
3.所有的火柴棍都必须被使用上。
本题的思路是对ABC三个数的值进行枚举,由于n<=24,并且等号和加号占去4根,那么还剩下20根,而在这能组成的数字里,1的使用最少火柴棍数量最少(两根),20根火柴棍最多只能组成10个1,那么每一个数不能够超过1111.那么我们在枚举中每一个数的过程中,如果每一个数所用的火柴棍的总数加起来等于m-4,那么我们就找到了一组解,但是我们需要注意的是,可以不用枚举出B,我们可以通过A+B的方式来计算出C,最后计算火柴棍的总数,这里可以有效减少计算的次数
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <ctype.h>
int fun(int x)//函数用来获取火柴棍的数量
{
int num=0;
int f[10]={6,2,5,5,4,5,6,3,7,6};
while(x/10!=0)//两位数的情况
{
num+=f[x%10];
x=x/10;//丢掉末尾数字
}
num+=f[x];
return num;
}
int main()
{
int a,b,c,m,sum=0;
scanf("%d",&m);
for(a=0;a<=1111;a++)
{
for(b=0;b<=1111;b++)
{
c=a+b;
if(fun(a)+fun(b)+fun(c)==m-4)
{
sum++;
printf("%d+%d=%dn",a,b,c);
}
}
}
printf("一共可以拼出%d个火柴棍等式",sum);
return 0;
}
最后
以上就是微笑路灯最近收集整理的关于算法(枚举)的全部内容,更多相关算法(枚举)内容请搜索靠谱客的其他文章。








发表评论 取消回复