[论文阅读] A novel binary shape context for 3D local surface descriptionA novel binary shape context for 3D local surface description

A novel binary shape context for 3D local surface description

Binary Shape Context (BSC) descriptor

二进制上下文描述子

2 BSC for 3D local surface description

2.1 Binary shape context descriptor In

2.1.1. Adaptive-scale keypoint detection

遍历所有的点云，在每个点邻域r的球体内，计算协方差，并PCA分解之。当三个特征值两两间的比值比较大时，认为是特征点。

一句话：找那些分布崎岖的点。

2.1.2. Local reference frame construction

LRF的构建具有重要意义。

• 旋转不变性
• 二义性通过遍历计算来进行消除。

协方差矩阵的计算是通过特征点，取其邻域r内的点来计算

$p$：特征点

$r^{(scale)}$：以特征点为球心的搜索半径。由上一步确定。

$N=q_0,q_1,...,q_m$：点集合，最前面的$q_0$就是特征点$p$,后面则是半径r内的所有点。m是周围的点的数量。

1. 对于点集的除特征点外所有的点，计算两个权重，分别是${\omega }_j^{(density)}$,${\omega }_j^{distance)}$

对于${\omega }_j^{(density)}$

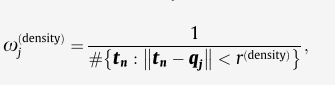
该权重用于补偿变化的点密度，因此点密度低的区域中的点比密度高的区域中的点贡献更大。

其中，
$$r^{(density)}=0.5r^{(scale)}$$
整个分母表示为：在半径$r^{(density)}$的范围内的点的数量。

因此，对于一个密度比较大的点来说，它的分母会很大，这就导致它的密度系数变小。而密度小的地方，分母也小，对应的这个点的密度权重就会变大。

目的：为了能够更好的从全局来描述

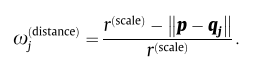
p是特征点，q离特征点越远，$||--||$里的内容越大，分子越小，权重越小。

所以该权重和距离成反比。越远，权重越小。

2. 整个协方差矩阵$M$的计算，充分考虑到了上面两个权重的参与：
   

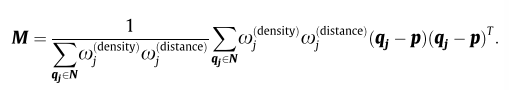
然后说到关于特征向量的二义性。才去的方法和大多数的人的类似，都是挨个对比，选取配对最优的解。

2.1.3. Local surface coordinate transformation

这里比较简单，就是把计算出来的局部坐标转换到(0,0,1)(0,1,0)(0,0,1)坐标系下。为了后续的往XoY各个平面上的投影做准备。

2.1.4. Projection-feature calculation

将转化到标准坐标系下的点云进行投影。xy xz yz 三个平面。

原始的点集：N

归一化到特征点的点集：N‘

分别往三个平面上投影：

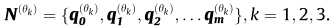
获得新的三个点集。

投影的栅格为S×S格的二维平面。

接下来，通过累积相应面元中每个点的特征，获得每个面元的投影点密度特征和投影点距离特征

注意，如图4所示，直接累积邻近点的相应特征会导致噪声敏感性、边界效应和LRF扰动。

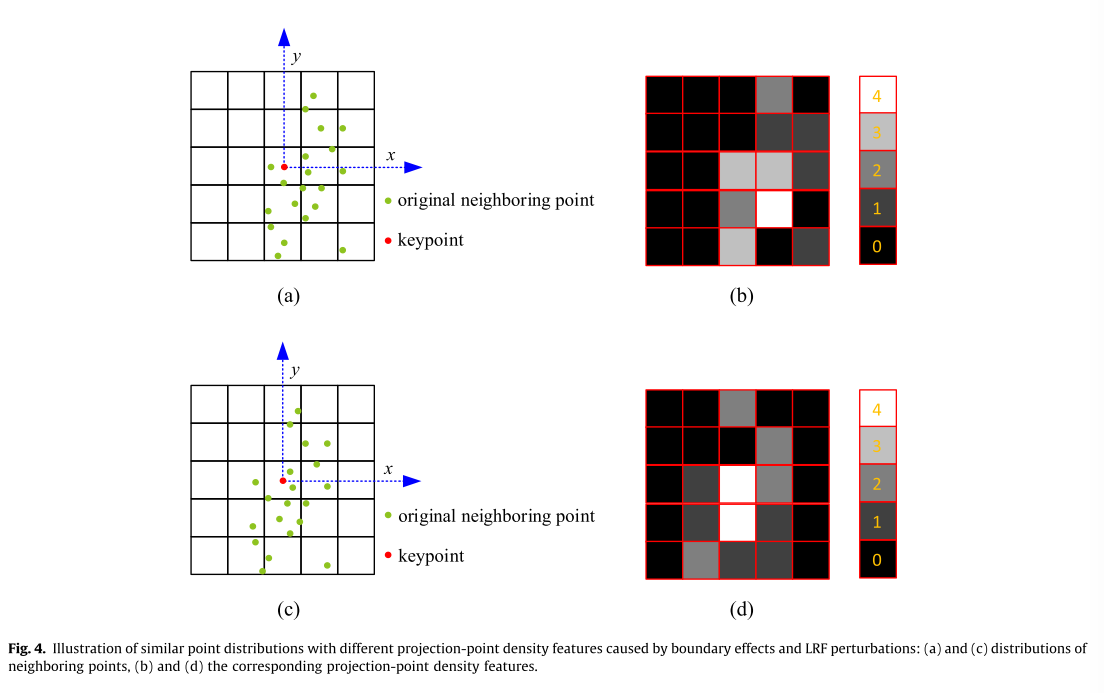
左边的是点的投影分布。右边的是对应的投影点密度特征。直接累加每个栅格内落入了多少个点。

以上是密度矩阵。还有一个距离矩阵，就是该点到平面的距离

可以看到分布相似，但是实际计算出来的 投影密度特征相差很大。

所以在这里引入了。高斯核密度估计。来计算每个点的加权投影密度和距离

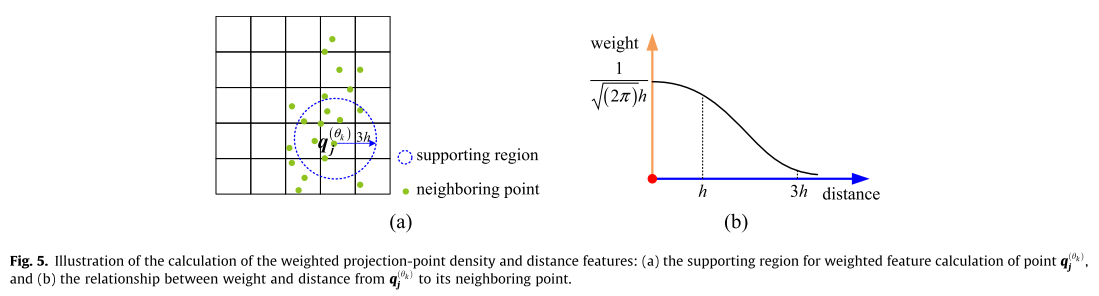
这个公式的直观理解就是该点和周围的每一个点的一个距离系数。当距离为0时，就是累加$\frac{1}{2\pi h}$，然后随距离递减。

其加权计算公式如下：

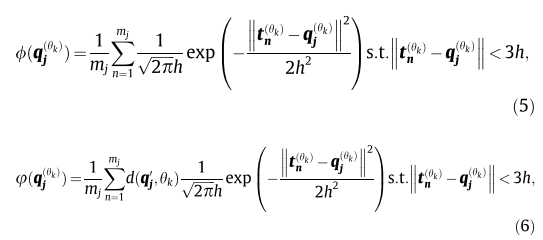
(5)：该点的加权投影密度值

(6)：该点的加权投影距离值

$t_n^{({\theta }_k)}$要求的点的3h范围附近的所有点。

…省略几个公式。

到目前为止，以上公式都是计算的每个点的距离权重和密度权重。那么如何投影到平面以获得这种黑白的栅格图呢？如下所示：

这里需要注意的是，经过上面的操作，所有的点只有两个属性，一个是距离权重，一个是密度权重。后面的往栅格上的投影，都是计算每个栅格上的这两个权重值。

然后就可以计算每一个栅格的加权投影点 **距离特征和密度特征。**计算公式如下：

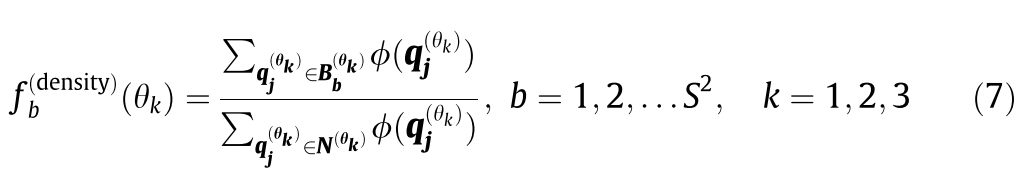
q是点Bb是当前这个bin的集合

这个地方相当于是分子分母归一化。

分母是计算当前平面内所有的范围在3h以内的点集的权重和。

分子是只计算当前栅格内的点的权重和。

然后依次计算$S^2$个栅格。

距离权重的计算相同！

需要说明的是，这种方法不仅解决了上面提及的边界问题，特征向量漂移问题。还能够解决相似的分布，但是点云的密度不同，其计算出来的投影矩阵是类似的。

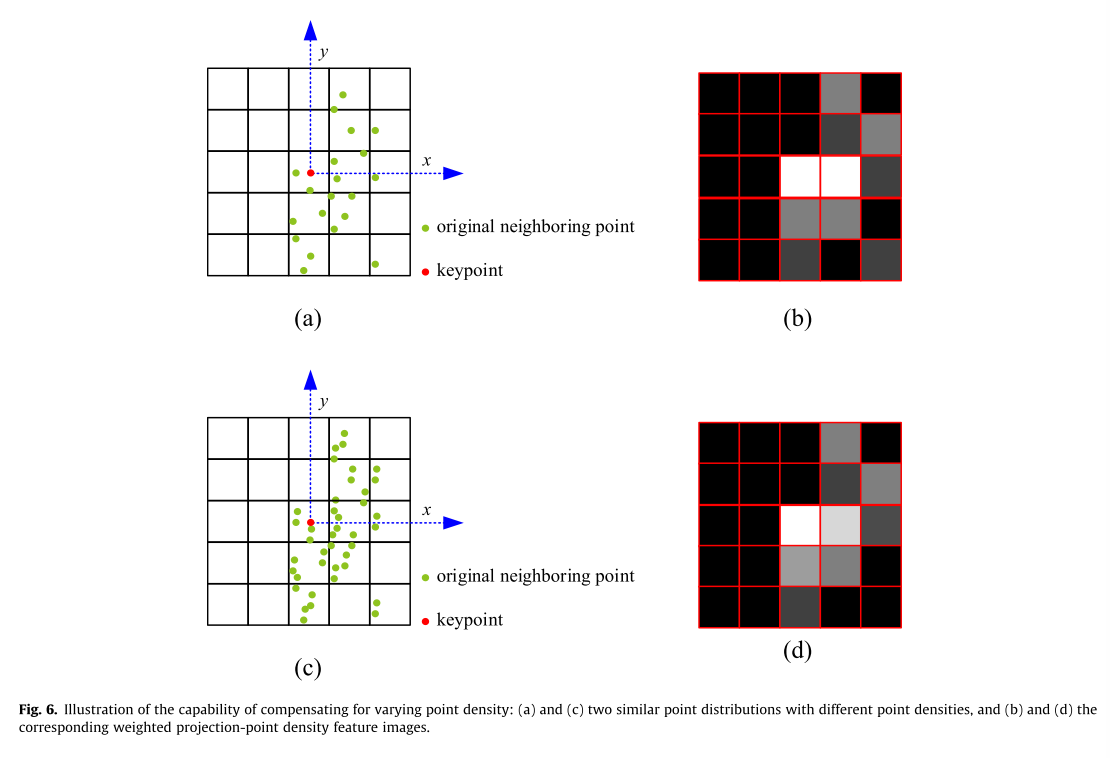
然后，本文为了可视化每一个栅格，生成了一个 特征图！

这个公式并不参与后面的计算，只是为了单纯的显示使用

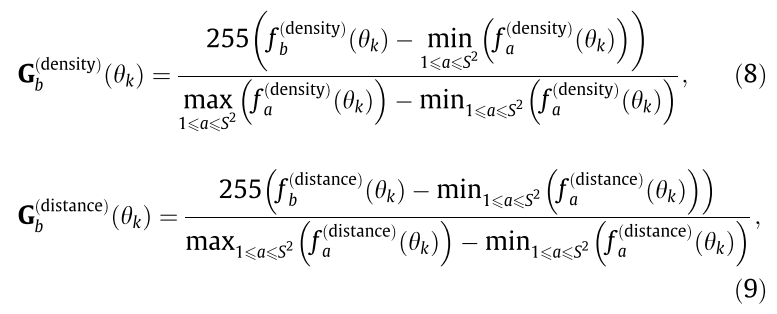
两个大G代表最后的计算灰度值。

$255\ast (0,1)\in (0,255)$

其中分母是max-min 分子是f-fmin。操作类似归一化。

越亮的地方点越多。代表灰度值越高。正好映射0代表黑色。

2.1.5. Projection features difference test

特征二值化

目的：特征二值化可以显著提高特征存储和匹配的效率，满足大规模点云数据快速配准和目标提取的需求。本文利用特征差异性测试实现上述投影特征的二值化，特征差异测试随机选择两个格子并计算它们特征的差异性，如果特征之间存在显著差异，那么测试结果为1，否则为0。对于每个投影面上的N个格子，存在C_2_N（N个格子，两两配对）种差异性测试，对所有格子的两两详尽组合进行差异测试非常耗时，并导致特征维数高、内存效率低。实验中发现，当差异性测试的数量较小时，增加其数量可以显著提高描述子的表达能力；进一步增加其数量不会向描述子添加任何重要的信息。因此，从C_2_N种差异性测试中随机选择一定数量的子集可以在不削弱描述子表达能力的前提下，降低时间和内存消耗。

以xoy 投影面上的投影距离特征为例，详细介绍其二值化的方法:

1. 从$C_N^2$种组合中，随机选择$g$对bins。组成一个集合$C$ 如下所示：

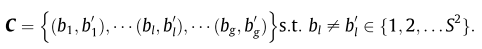
这个地方的意思是，在$S^2$个bins里面，随即挑选一部分子集，进行差异性测试。

然后比如有两个需要对比的特征，一个带丿一个不带丿。两个特征对应的bin，进行值的差值计算。

选取g个。

也就是说，任意两个特征在进行对比的时候，都是只选一部分bin来进行对比，优点有2个：

1.减少计算量和内存消耗

2.一定数量的bins就已经足够表达当前特征了。

2. 对集合中的任意两个格子$(b_i,b_i^{{}^{\prime }})$根据一下公式进行差异性测试。把投影特征转化为一个二进制字符串。
   
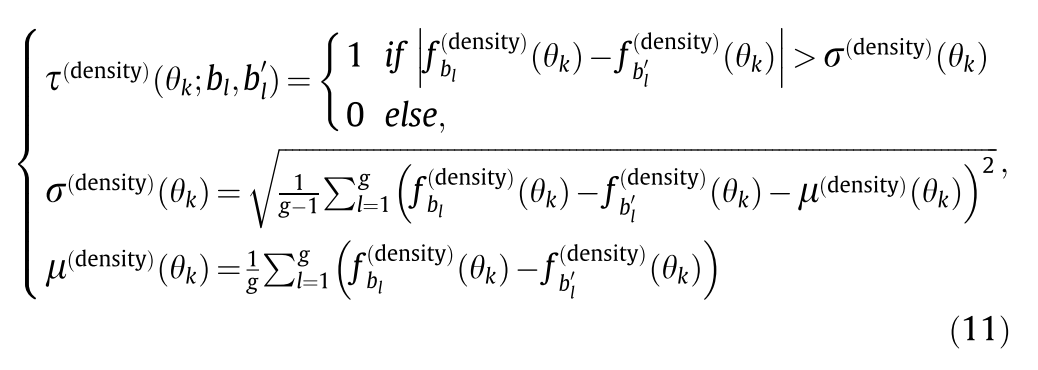
   这个公式(11)需要从下往上看。

这里的意思是，对于$S^2$个栅格，不用全都计算差异性，而是随机选择一些进行计算，然后组成描述子

这就是自己和自己匹配。随机挑选对，算出来一个阈值。然后每个pair相似与否根据这个阈值来确定。

相同的描述子，因为匹配的配对的index是固定的，所以最后计算出来的二进制字符串也是一样的。所以是可以自圆其说的。

2.2 BSC generation parameters

后续是关于各个参数是怎么获得的。这里不再展开赘述。

最后

以上就是俏皮水池为你收集整理的[论文阅读] A novel binary shape context for 3D local surface descriptionA novel binary shape context for 3D local surface description的全部内容，希望文章能够帮你解决[论文阅读] A novel binary shape context for 3D local surface descriptionA novel binary shape context for 3D local surface description所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。