乘法逆元通俗易懂的理解方法

最近，发现数论真的很重要，基本上一套题必出一个数论的题。故接下来，要好好的看一看数论了。

乘法逆元我觉得其本质：就是数论里的倒数。

由上图你会发现：其取模的运算不满足除法的分配律，那么如何求除法的模运算呢？

在我们普通的数学中：
要求 a / b 可以转化为 a x b^-1 其中 b x b^-1 = 1 ，其中 b^-1 称为b的倒数。

那么同理,在数论我们可不可以用上面的那种方法来求b的类似于倒数的数，来将其转换为乘法呢?

答案: 是肯定的，不过在数论里称为乘法的逆元。

有的小伙伴可能初学，不太懂上面的专业术语，故这里解释一下。
上面定义的解释: 上面的那个三条线的符号是同余, 意思就是说 a乘于x取模 和 1 取模是同余的都是1，即余数是相同的。
例子:
2 x 3 ≡ 1 （mod 5 ) 即 2 x 3 对 5 取模和 1 对 5 取模是同余的 都是1 。 其中 3就是 2的乘法逆元。
实战：

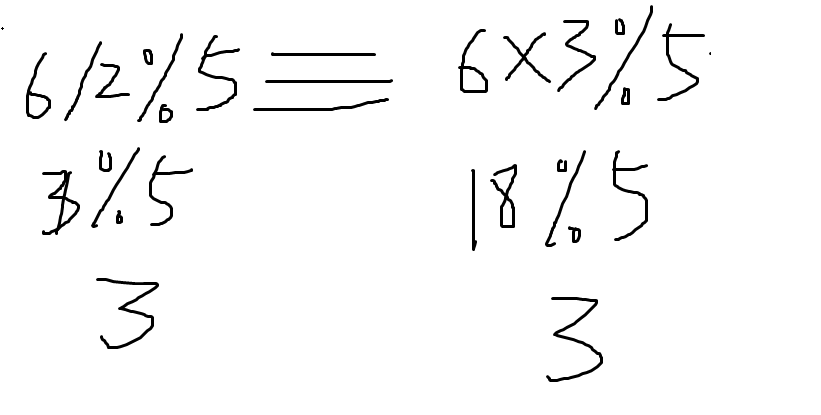
你会发现: 我们运用乘法逆元，将其除法变成了一个乘法。这是十分的方便的，尤其是涉及到高精度或者其它的一些情况。

那么，问题来了。如何求一个数的乘法逆元呢？

求乘法逆元的方法有很多，这里先介绍通过运用费马小定理来求逆元。

a^p-1 ≡ 1 （mod p ) 等价于 a x a^p-2 ≡ 1 （mod p ) 故a的乘法逆元就是 a^p-2
注意：乘法逆元不一定是存在的。
a 存在乘法逆元的充要条件是 a 与模数 p 互质。当模数 p 为质数时，a^p−2 即为 a 的乘法逆元。

练习题：876. 快速幂求逆元

https://www.acwing.com/problem/content/878/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<cstdio>
#include<iostream>
using namespace std;
typedef long long int LL;
LL quick_pow(LL a,LL b, LL p)
{
    LL res=1;
    while(b)
    {
        if(b&1)  res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
LL gcd(LL a, LL b)
{
    if(b==0) return a;
    else return gcd(b,a%b);
}
int main(void)
{
    LL t,a,p; cin>>t;
    while(t--)
    {
        cin>>a>>p;
        if(gcd(a,p)==1) cout<<quick_pow(a,p-2,p)<<endl;
        else cout<<"impossible"<<endl;
    }
}

最后

以上就是正直海燕最近收集整理的关于乘法逆元通俗易懂的理解方法的全部内容，更多相关乘法逆元通俗易懂内容请搜索靠谱客的其他文章。