逆元求组合数

43 阅读 0 评论 29 点赞

我是靠谱客的博主友好八宝粥，最近开发中收集的这篇文章主要介绍逆元求组合数，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目

给一个歌单固定长度为K
有两种歌：X首长度为A，Y首长度为B的歌，A!=B
问有几种组合搭配
如：
输入 K = 5，A = 2 X = 3 B = 3 Y = 3
输出 9
由于结果比较大，因此输出结果取1000000007的余数。

思路

腾讯春招实习笔试题……用自己的方法瞎做最后发现除数那里的取余不知道怎么取。

问了yz大佬，给我一篇博客，大概是“逆元求组合数”“费马小定理”。

快速幂
百度百科上的解释

快速幂就是不同于平时一个数一个数相乘求幂的方法，举个例子，求a ^ b(a的b次方)：

a ^ 11 = a ^ ( 2 ^ 0 + 2 ^ 1 + 2 ^ 3) = a ^ (2 ^ 0) + a ^ (2 ^ 1) + a ^ (2 ^ 3)

也就是把右上角的次方：11拆成二进制表达方式： 2 ^ 0 + 2 ^ 1 + 2 ^ 3 == 1011
快速幂取模算法

笔试的时候我是粗暴使用了上面博客直接取模第3种的方法。

这里的快速幂需要知道以下公式：


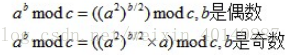
// 依照上面公式，不考虑取模的写法如下：
// a^b
int power_mod(int a, int b) {
    int ans = 1;
    while (b) {
        if (b%2) {
            ans *= a;
        }
        b /= 2;
        a *= a;
    }
    return ans;
}

// 或者用位运算
int power_mod(int a, int b) {
    int ans = 1;
    while (b) {
        if (b & 1) {
            ans *= a;
        }
        b >>= 1;
        a *= a;
    }
    return ans;
}

// 取模版本:
int power_mod(int a, int b, int c) {
    int ans = 1;
    a %= c;
    while (b) {
        if (b & 1) {
            ans *= a;
            ans %= c;
        }
        b >>= 1;
        a *= a;
        a %= c;
    }
    return ans;
}

逆元

逆元：对于a和p（a和p互素），若a*b%p≡1，则称b为a%p的逆元。

费马小定理

假如a是一个整数，p是一个质数，那么 a^p-a 是p的倍数：

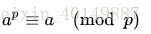
如果a不是p的倍数：

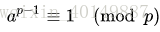
=> a^(p-2) * a % p = 1
=> a * a^(p-2) % p = 1

因此， a^(p-2)也是
求组合数取模

组合数的求法：

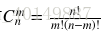
除法的取模和乘法不同，逆元和费马小定理可以帮助求组合数的取模。

求(a/b) %p，若已知b%p的逆元是c=> b*c%p = 1，

(a/b) %p = ((a*c%p)/(b*c%p))%p = (a*c%p)%p = (a%p)(c%p)%p

求解方法：
1. 先算出n!%p、m!%p、(n-m)!%p，用fac[i]表示 i!%p 的值
2. 因为组合数取模是(n!)/(m!(n-m)!)%p，因此需要计算出m!%p、(n-m)!%p的逆元，根据费马小定理，m!%p、(n-m)!%p的逆元分别是(m!)^(p-2)、((n-m)!)^(p-2)
3. 快速幂取模求出(m!)^(p-2)%p、((n-m)!)^(p-2)%p，分别记为M、NM
4. 最后求一下(n!)%p * M * NM % p

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include <cstring>

using namespace std;



long long power_mod(long long a, long long b, long long c) {
    long long ans = 1;
    a %= c;
    while (b) {
        if (b & 1) {
            ans = ans * a % c;
        }
        b >>= 1;
        a = a * a % c;
    }
    return ans;
}



int main() {
    long long fac[1000] = {1}, n, m, p = 10007, k;
    for (int j = 1; j < 1000; j++) {
        fac[j] = fac[j-1] * j % p;
    }
    cin >> k;
    for (int i = 0; i < k; i++) {
        cin >> n >> m;
        cout << fac[n] * power_mod(fac[m], p-2, p) % p * power_mod(fac[n-m], p-2, p) % p << endl;
    }
}

提交到niop可以通过。

以上整理自：

http://www.cnblogs.com/wuyudong/p/3637479.html
https://www.cnblogs.com/liziran/p/6804803.html
https://baike.baidu.com/item/%E5%BF%AB%E9%80%9F%E5%B9%82
https://en.wikipedia.org/wiki/Fermat%27s_little_theorem