逆元相关

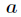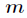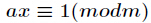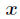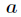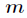首先是逆元的概念： 对于正整数和，如果有，那么把这个同余方程中的最小正整数解叫做模的逆元。

首先是这个同余符号≡
含义
两个整数a，b，若它们除以整数m所得的余数相等，则称a，b对于模m同余
记作a≡b(mod m)
读作a同余于b模m，或读作a与b关于模m同余。
比如26≡14(mod 12)。

逆元的一种用法是

可以使用逆元将除法转换为乘法： 即，除以一个数取模等于乘以这个数的逆元取模。

除法求模不能类似乘法，对于（A/B）mod C，直接（A mod C）/（B mod C）是错误的,找到B的逆元b(b=B^-1);求出(A*b)modC即可；

由费马小定理：B 关于 P 的逆元为  B^(p-2);

找了个练习题 lightoj1067

题目大意就是让你求组合数，只是组合数会很大所以要用到逆元

然后我用快速幂和拓展欧几里得分别写了写。

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#include <set>
#include <stack>
#define fuck() (cout << "--------------------------------" << endl)
#define mod 1000003
using namespace std;
const int maxn = 1000000 + 5;
const int inf = 0x3f3f3f3f;
long long jiecheng[maxn];
long long niyuan[maxn];

long long  exgcd(long long a, long long b,long long &x, long long &y)
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    long long  d = exgcd(b,a%b,y,x);
    y -= a/b*x;
    return d;
}
long long modreverse(long long a, long long MOD)
{
    long long x;
    long long y;
    int d = exgcd(a,MOD,x,y);
    if(d == 1)
        return (x%MOD+MOD)%MOD;
    return -1;
}
//long long  qumo(long long a, long long b)  快速幂函数，分治法
//{
//    if(b == 0) return 1;
//    long long  x = qumo(a,b/2);
//    long long ans = x*x%mod;
//    if(b%2 == 1) ans = ans*a%mod;
//    return ans;
//}
void init()
{
    jiecheng[0] = 1;
    niyuan[0] = 1;
    for(int i=1; i<maxn; i++)
    {
        jiecheng[i] = jiecheng[i-1]*i%mod;
        niyuan[i] = modreverse(jiecheng[i],mod);
        //niyuan[i] = qumo(jiecheng[i],mod-2); 快速幂方法
    }
}
int main()
{
    int T;
    cin >> T;
    int kase = 1;
    init();
    while(T--)
    {
        long long a,b;
        cin >> a >> b;
        long long ans = ((jiecheng[a]*niyuan[b]%mod)*niyuan[a-b])%mod;
        printf("Case %d: %lldn",kase++,ans);
    }
}

最后

以上就是单身电话为你收集整理的逆元相关的全部内容，希望文章能够帮你解决逆元相关所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。