LIME：算法讲解

目录

一、简介

 1. 主要用途

2. 样例分析

二、基础理论

1. 对解释器算法的要求

2. 算法原理

3. 算法实现

4. 算法流程

三、 优缺点分析

优点

缺点

一、简介

        LIME算法是Marco Tulio Ribeiro2016年发表的论文《“Why Should I Trust You?” Explaining the Predictions of Any Classifier》中介绍的局部可解释性模型算法。该算法可以用在文本类与图像类的模型中，以分析模型提取到的特征是否符合直观理解。

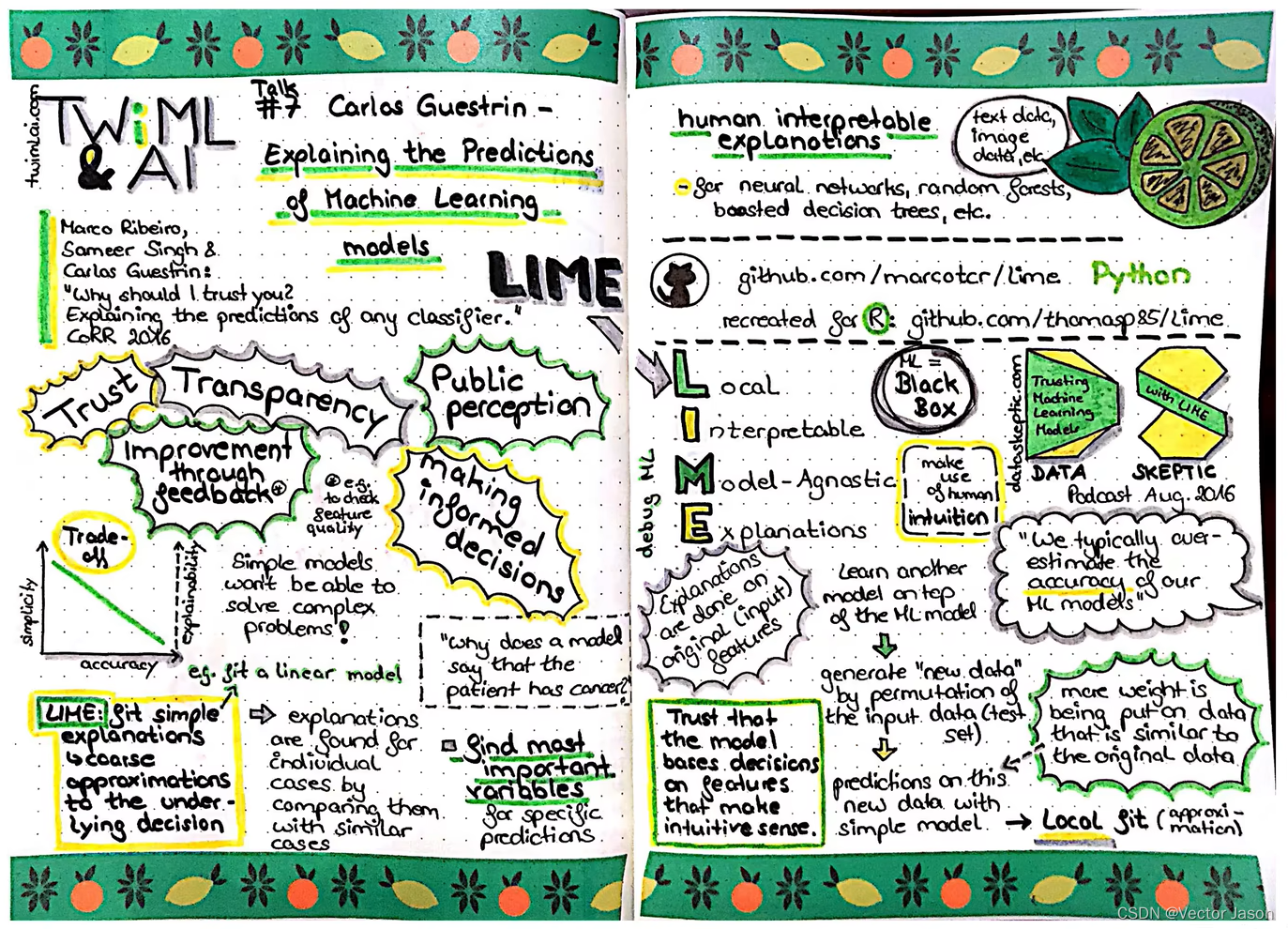
 1. 主要用途

        在实际建模过程中，我们不仅需要使客户能够信服，同时也需要使自己信服。如果仅仅以数字，描述一个系统的性能，则显得略有偏颇，比如神经网络普遍可以达到高性能的效果，但可解释性低，因此如果能够从模型本身的底层逻辑出发，以它的视角观察事物，分析事物，解释事物，便可以明确模型的性能为什么好，为什么不好。这种时候，就可以利用本文要介绍的LIME算法，全称Local Interpretable Model-agnostic Explanations，可以理解为模型的解释器。

2. 样例分析

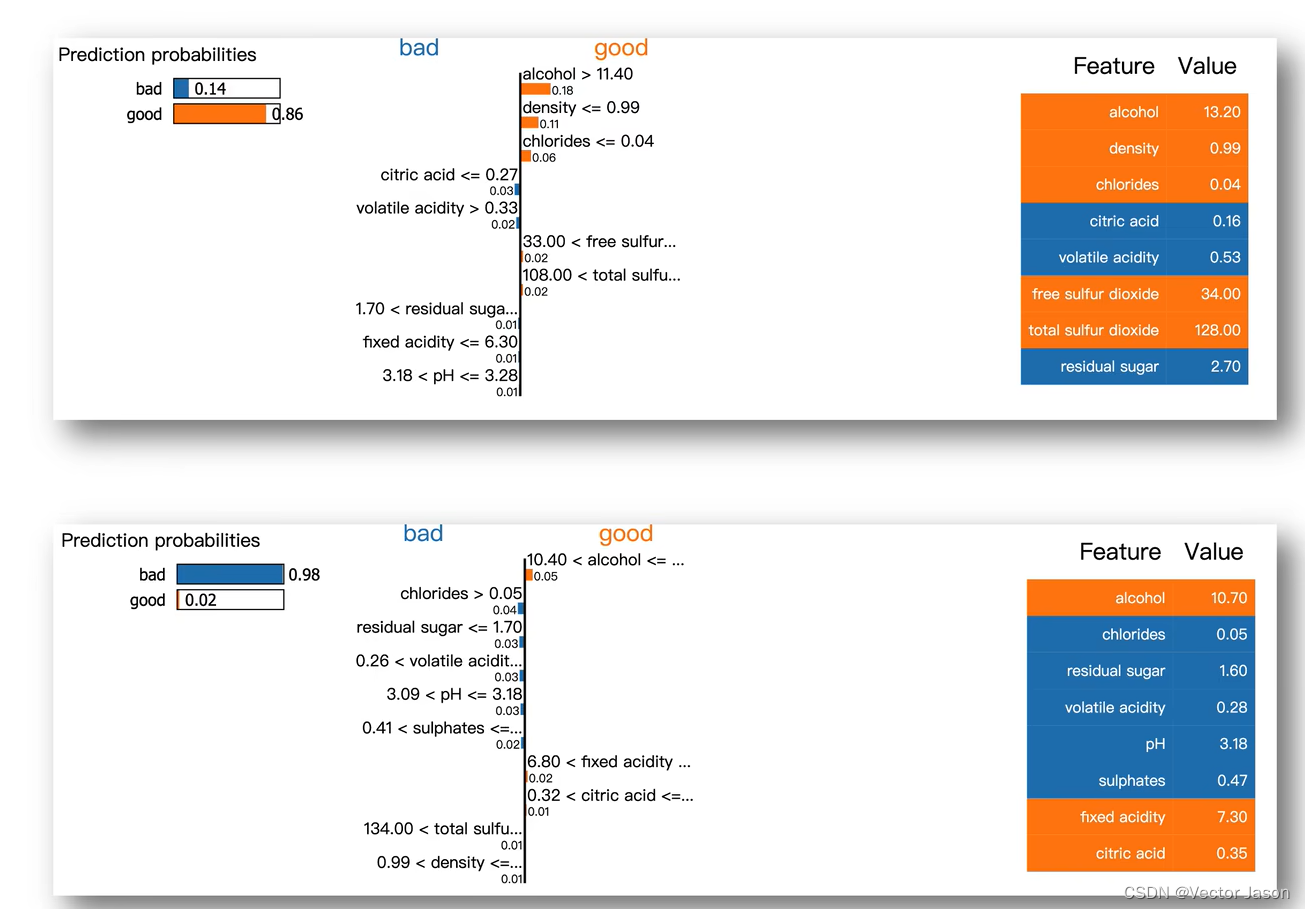
         一瓶葡萄酒的品质将对售卖价格产生直接影响，通过分析其化学成分，即可明确某一瓶葡萄酒的品质。通过LIME，从葡萄酒的可解释特征中分析得出，当alchol>11.4时将对其品质产生正向影响，真正做到搞清楚模型为什么认为好还是不好。

       根据一封邮件的文本内容，判断发信者是与“基督教“有关还是与”无神论教“有关，分类器本身达到了90%的准确率。但是利用LIME解释器，发现”无神论教“的重要特征，是”Posting“(邮件标头的一部分)，这个词与无神论本身并没有太多的联系。这意味着尽管模型准确率很高，但所学习到的特征是错误的。

二、基础理论

1. 对解释器算法的要求

可解释性
        解释器的模型与特征都必须是可解释的，像决策树、线性模型因其严格的数学推导都是很适合拿来解释的模型；而可解释的模型必须搭配可解释的特征，才是真正的可解释性，让不了解机器学习的人也能通过解释器理解模型。

局部保真度
        在实际情况中，解释器不需要在全局上达到复杂模型的效果，但至少在局部上效果要很接近，而此处的局部代表我们想观察的那个样本的周围。

泛化性强
        这里所指的是与复杂模型无关，换句话说无论多复杂的模型，像是SVM或神经网络，该解释器都可以工作，都能进行可解释性分析。

2. 算法原理

        对于一个分类器（复杂模型），想用一个可解释的模型（简单模型如线性规划），搭配可解释的特征在全局上进行分析是极其困难的，相反，如果我们能在某一局部的决策边缘上验证其可解释性，即可说明该分类器的优越性能。

        具体来说，我们从加粗的红色十字样本（待解释样本）周围采样，所谓采样就是对原始样本的特征做一些扰动，将采样出的样本用分类模型分类并得到结果（红十字和蓝色点），同时根据采样样本与加粗红十字的距离赋予权重（权重以标志的大小表示）。虚线表示通过这些采样样本学到的局部可解释模型，在这个例子中就是一个简单的线性分类器。在此基础上，我们就可以依据这个局部的可解释模型对这个分类结果进行解释了。

3. 算法实现

（1）目标函数

        解释模型定义为模型g∈G，我们进一步使用作为实例z与x之间的接近度，以定义x周围的局部性。定义一个目标函数ξ，这里的L函数作为一个度量，描述如何通过在局部定义中，g如何逼近f（复杂模型），在当Ω(g)(解释模型复杂度)足够低可以被人类理解时，我们最小化L函数得到目标函数的最优解。LIME产生的解释如下：

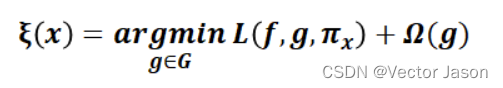
 (2)引入自适应相似度后的目标函数

        考虑到离待解释样本距离不同的扰动样本附加权重理应不同，引入自适应相似度，即optim-LIME的目标函数如下：

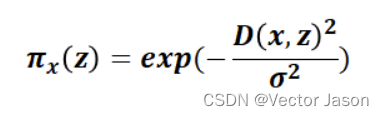
 （3）最终函数

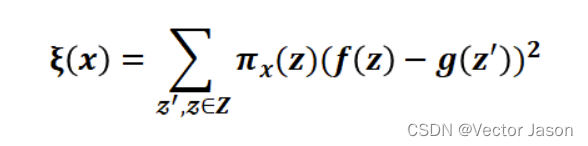
        其中f(z)是扰动样本在d维空间（原始特征）上的预测值，g(z’)则是在d’维空间（可解释特征）上的预测值，然后以相似度作为权重，因此上述的目标函数便可以通过线性回归的方式进行优化。

4. 算法流程

宏观来看：

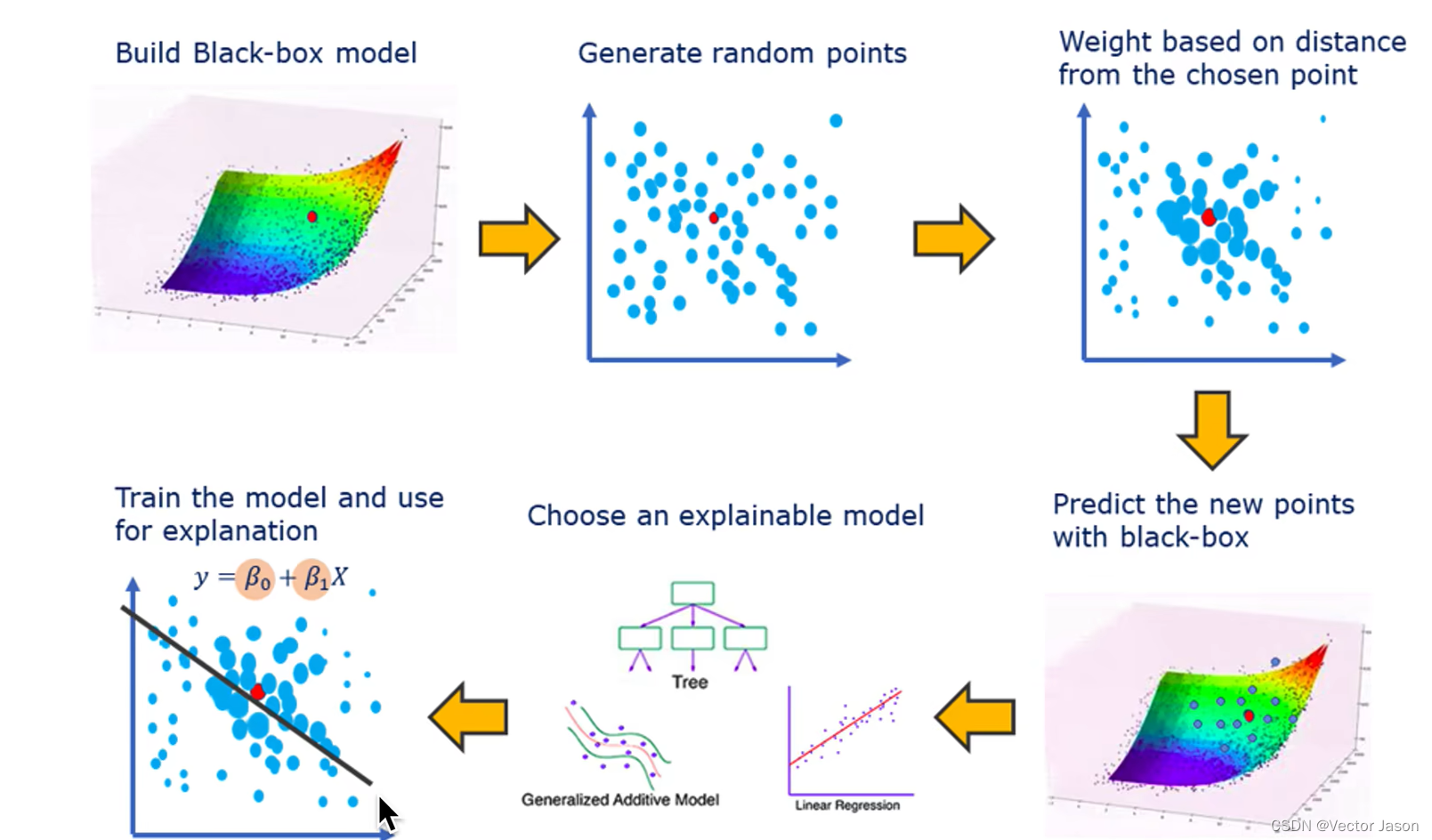
        首先，在待解释的模型中取一个待解释样本，之后随机生成扰动样本，并以与待解释样本的距离作为标准附加权重，再将得到的结果作为输入投入待解释模型中，同时选择在局部考察的待训练可解释模型（如决策树、逻辑回归等等），最终即可训练出在可解释特征维度上的可解释性模型。 

微观来看：

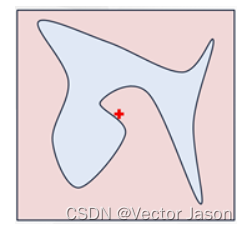
         选取待解释样本X，并转换为可解释特征维度上的样本X’。

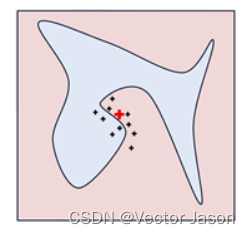
        通过随机扰动，得到其余在可解释特征维度上的样本Z’。

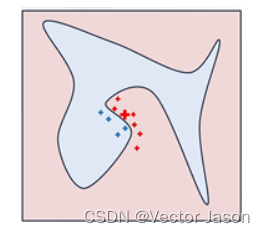
         将Z’恢复至原始维度，计算f（z）与相似度。

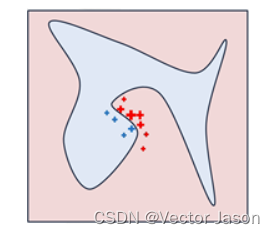
         利用自适应相似度对各个样本点进行加权。

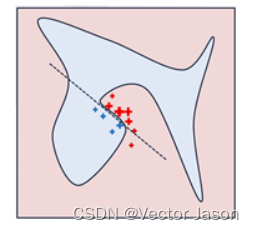
         以X’作为特征，f（z）作为标准训练局部可解释模型（如图虚线）。

三、 优缺点分析

优点

        1. 具有很强的通用性，性能优越

        LIME能够兼容任何一种机器学习算法，具有广泛的适用性。LIME除了能够对图像的分类结果进行解释外，还可以应用到自然语言处理的相关任务中，如主题分类、词性标注等。

        2. 针对性强，可塑性好

        LIME可以选取代表性样本进行训练，降低了工作量和难度，也能够依照客户灵活的需求进行特殊场景的分析，如调节某一特征的权重，分析其变化对最终结果的影响程度。

缺点

         1. 局部性不可代表全局性

        LIME从局部出发训练可解释性模型，当全局决策范围具有极其复杂的非线性时，局部线性区域范围小，仅能对极少的样本进行可解释分析。

        2. 时间成本高

        对每一个待测样本进行可解释分析时，需重新训练对应的可解释模型，训练时间长。

最后

以上就是可靠斑马为你收集整理的LIME：算法讲解的全部内容，希望文章能够帮你解决LIME：算法讲解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。