题目
根据式(5.18)和(5.19),试构造一个能解决异或问题的单层RBF神经网络。
- 式(5.18): ϕ ( x ) = ∑ i = 1 q w i ρ ( x , c i ) phi(x)=sum_{i=1}^qw_irho(x,c_i) ϕ(x)=∑i=1qwiρ(x,ci)
- 式(5.19): ρ ( x , c i ) = e − β i ∣ ∣ x − c i ∣ ∣ 2 rho(x,c_i)=e^{-beta_i||x-c_i||^2} ρ(x,ci)=e−βi∣∣x−ci∣∣2(高斯径向基函数)
第k个样本的错误率为
E
k
=
1
2
(
ϕ
(
x
)
−
y
k
)
2
E_k=frac12 (phi(x)-y^k)^2
Ek=21(ϕ(x)−yk)2。
异或问题共有4个样本(0, 0, 0)、(0,1,1)、(1,0,1)、(1、1,0)
RBF网络有三类参数,假设RBF网络隐层有t个神经元:
- w i w_i wi:第i个隐层神经元对应的权重。t个神经元的输出用w线性结合得到RBF网络的输出。
- c i c_i ci:第i个隐层神经元所对应的中心。 c i c_i ci是与输出的单个样本一样长的向量,可以通过随机采样和聚类的等方法,这里只有4个数据,使用随机采样。
- β i beta_i βi:
这里用到的RBF函数是高斯径向基函数,也可以有其他的径向基函数。RBF的训练的思想就是,若输入的数据和神经元的中心点越相似即越靠近 ( ∣ ∣ x − c i ∣ ∣ 2 ) (||x-c_i||^2) (∣∣x−ci∣∣2),则高斯径向基函数的值就越大( e − β i ∣ ∣ x − c i ∣ ∣ 2 e^{-beta_i||x-c_i||^2} e−βi∣∣x−ci∣∣2),所有隐层神经元的输出通过带权重的投票( ∑ i = 1 q w i ρ ( x , c i ) sum_{i=1}^qw_irho(x,c_i) ∑i=1qwiρ(x,ci))来决定最后输出结果。
梯度:
- ∂ E k ∂ w i = ( ϕ ( x ) − y k ) ρ ( x , c i ) frac{partial E_k}{partial w_i}=(phi(x)-y^k)rho(x,c_i) ∂wi∂Ek=(ϕ(x)−yk)ρ(x,ci)
- ∂ E k ∂ β i = − w i ( ϕ ( x ) − y k ) ρ ( x , c i ) ∣ ∣ x − c i ∣ ∣ 2 frac{partial E_k}{partial beta_i}=-w_i(phi(x)-y^k)rho(x,c_i)||x-c_i||^2 ∂βi∂Ek=−wi(ϕ(x)−yk)ρ(x,ci)∣∣x−ci∣∣2
通过梯度下降法来更新参数。
RBF的内容推荐看"林轩田机器学习技法"的相关章节。
代码
import numpy as np
import matplotlib.pyplot as plt
def getDataSet():
"""
得到异或的训练集
:return:
"""
dataSet = [
[0, 0, 0],
[0, 1, 1],
[1, 1, 0],
[1, 0, 1]
]
return np.array(dataSet)
def RBFNN(dataSet, eta, thresh):
"""
训练RBF网络
:param dataSet: 数据集
:param eta: 学习率
:param thresh: 错误率容忍度
:return: w, 隐层神经元对应的权重
c, 隐层神经元对应的中心
beta, 高斯径向基函数里的参数
errHistory 训练的历史错误率
"""
errHistory = [] # 记录每轮迭代的均方误差
y = dataSet[:, -1]
x = dataSet[:, :-1]
m, n = x.shape
# 隐层神经元数
t = 10
# 初始化c
c = np.random.rand(t, n)
# 初始化beta
beta = np.random.randn(1, t)
# 初始化w
w = np.random.rand(1, t)
err = errOfMeanSqur(dataSet, w, c, beta)
while err > thresh:
for i in range(m):
trainX = np.tile(x[i], (t, 1))
dist = ((trainX - c) ** 2).sum(axis=1).reshape(1, -1) # 1 x 8
rho = np.exp(-beta * dist) # 1 x 8
phi = np.dot(w, rho.T)
# 计算梯度
dBeta = -w * (phi - y[i]) * rho * dist
dw = (phi - y[i]) * rho
# 更新参数
beta -= eta * dBeta
w -= eta * dw
# 计算新的错误率
err = errOfMeanSqur(dataSet, w, c, beta)
errHistory.append(err)
print(f"iteration {len(errHistory)}, err = {err}")
return w, c, beta, errHistory
def classify(data, w, c, beta):
"""
给定参数分类
:param data:
:param w:
:param c:
:param beta:
:return:
"""
dataArr = np.tile(data, (c.shape[0], 1))
dist = ((dataArr - c) ** 2).sum(axis=1)
rho = np.exp(-beta * dist).reshape(-1, 1)
return np.dot(w, rho)
def errOfMeanSqur(dataSet, w, c, beta):
"""
计算平方误差
:param dataSet:
:param w:
:param c:
:param beta:
:return:
"""
x = dataSet[:, :-1]
y = dataSet[:, -1]
num = x.shape[0]
err = 0.0
for i in range(num):
yPre = classify(dataSet[i][:-1], w, c, beta)
err += ((y[i] - yPre) ** 2) / 2.0
return (err / float(num))[0][0]
def main():
# test RBFNN(dataSet, eta, thresh)
dataSet = getDataSet()
w, c, beta, errHistory1 = RBFNN(dataSet, 0.1, 0.001)
plt.plot(np.arange(len(errHistory1)), errHistory1)
plt.show()
# 测试抑或
for data in dataSet:
pre = classify(data[:-1], w, c, beta)
print(f"data = {data[:-1]}, label = {data[-1]}, pre = {pre}")
if __name__ == '__main__':
main()
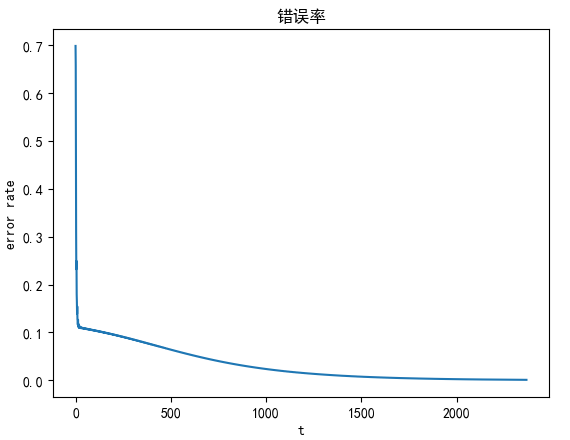
结果
迭代错误率
预测

最后
以上就是呆萌项链最近收集整理的关于西瓜书课后题5.7(单层RBF神经网络解决抑或问题)题目代码的全部内容,更多相关西瓜书课后题5内容请搜索靠谱客的其他文章。








发表评论 取消回复