$2^k$析因设计（factorial design）在QE中几乎是必考的内容，但经过上课作业考试以后感觉还是停留在入门的程度，不得已只能自学一下教材。$2^k$析因设计包括的内容是$2^k$析因设计的基本原理、Confounding和fractional $2^k$析因设计，分上下两篇博文介绍它们的概念和统计模型。

先澄清基本概念，$2^k$析因设计中的两个关键词，析因设计在UA MATH571B 试验设计V 析因设计简介中已经介绍过了，它与之前的RCBD最大的不同在于析因设计分析的treatment factor不止一个；$2^k$的含义是假设有$k$个treatment factor，那么每个factor我们只取两个factor level来做试验，一个level被称为high level，另一个被称为low level。

通常我们不会用$2^k$析因设计去做一个完整的试验，而是把它作为一个研究的预试验。它的好处是能够以较少的试验资源分析因子的重要性，帮助我们排除掉一些不重要的因子与效应，从而提高试验效率并构建更准确的统计模型。

$2^k$析因设计

先来学习一下$2^k$析因设计中的treatment effect的记号。假设我们想要研究四个treatment factor，那么只有一个factor为high level的effect我们记为：a,b,c,d；两个factor为high level的效应我们记为：ab, ac, ad, dc,db,cd；三个factor为high level的效应记为：abc, abd, acd, bcd；四个factor为high level的效应记为：abcd；比如a表示只有因素A为high level，BCD均为low level的effect；abd表示因素ABD均为high level，C为low level的effect，另外用(1)表示所有因素均为low level的effect。但通常我们不按照这个顺序排列，我们按standard order来排列这些effect：
$$(1),a,b,ab,c,ac,bc,abc,d,ad,bd,abd,cd,acd,bcd,abcd$$

按字母顺序排列，但新出现一个effect之后，要把它和以前的effect的组合也要写上去。

这张表给出了分析$2^k$析因设计试验结果的一般性步骤。首先计算treatment effect，然后用初始模型（full model，包含所有的effects和interactions）做一下统计分析，根据统计分析的结果，我们可以将不重要的factor或者interaction删去，从而优化统计模型，最后对优化后的模型进行分析，为后续试验提供指导。

因子效应的计算

在上面介绍的因子效应的表示方法使得每一个因子效应都可以表示成一个contract，以上面介绍的$2^4$设计为例，因子效应的一般表示为
$$(a\pm 1)(b\pm 1)(c\pm 1)(d\pm 1)$$

比如要计算因子$A$的效应就可以用
$$Contrac{t}_A=(a-1)(b+1)(c+1)(d+1)$$

比如因子$AC$的交叉效应可以表示为
$$Contrac{t}_{AC}=(a-1)(b+1)(c-1)(d+1)$$

展开后各项就是treatment effect，这种操作能够将因子效应用treatment effect表示出来（treatment effect是比较具体的，factor level combinations的effect）。根据Contract的性质可以把因子的平方和也计算出来，
$$S{S}_{AC}=\frac{1}{n{2}^4}Contrac{t}_{AC}^2$$

其中$n$是独立重复试验次数。这种计算表示方法可以推广至任意多个factor。

ANOVA table

下面是$2^k$析因设计的ANOVA table，有$n$次独立重复试验，$k$个factor的两个level共有$2^k$中组合方式，因此总的试验单位有$n{2}^k$。每种contract占一个自由度，因此所有的contract一种占$2^k$个自由度（就是上面contract的展开式的个数），所以残差的自由度为$2^k(n-1)$。当只有一次重复试验时，残差没有自由度，这时不能做ANOVA F检验；当有两个及两个以上自由度时，这时分析方法就是常规的ANOVA。

Single-replicate $2^k$析因设计

毕竟$2^k$析因设计只是一个预实验步骤，所以试验资源能省则省，很多时候就只能做一个重复试验，上面分析到只有一次重复试验时，ANOVA是没办法用的，那我们又应该用什么工具来分析试验结果呢？Daniel (1959)提出，我们可以用normal probability plot方法。根据上面已经介绍的方法，我们可以计算出因子效应的估计以及平方和。下图是一个示例，第三行的percent contribution指的是因子的平方和相对总平方和的比值，其实从这个图中我们已经可以看出点名堂了，显然因子B的contribution是非常小的，连带着包含B的交互效应也是比较小的。

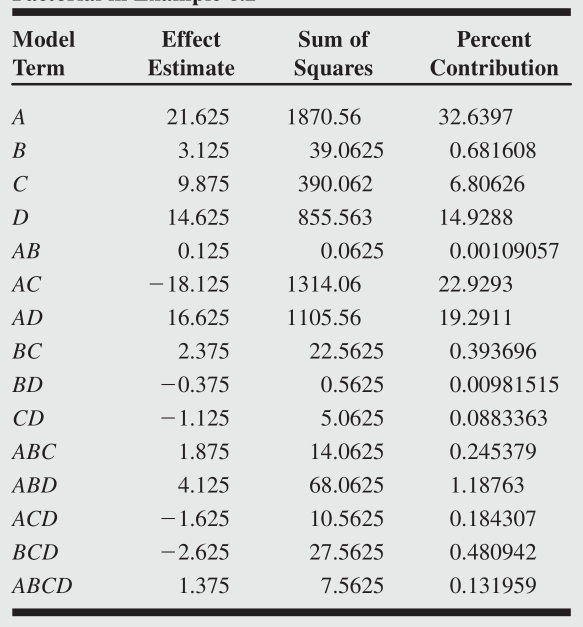
下面我们假设因子的效应（第一列）是正态（或者至少是位置-尺度参数族）的，记其分布函数为$F$，将其从上到下记为$e_1.\cdots ,e_{15}$，将其按从小到大的顺序排序，记顺序统计量为$e_{(1)},\cdots ,e_{(15)}$，它们对应理论概率估计值为（参考UA MATH571A 一元线性回归IV 模型诊断介绍的正态概率估计值）
$${\hat{p}}_i=F\left(\frac{e_i-\mu }{\sigma }\right)=\frac{i+0.375}{15+0.25},i=1,\cdots ,15$$

作出$(e_{(i)},{\hat{p}}_i)$的图像，这个就叫正态概率图（normal probability plot），这个例子的正态概率图如下图所示

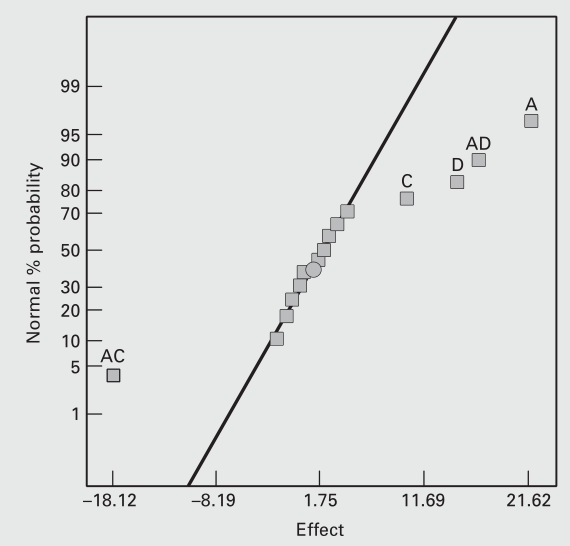
比较集中的那些因子效应说明都是不显著的，我们可以把他们排除掉。位置比较偏的这几个效应是显著的，我们要保留下来，因此因子A，C，D，AC，AD被保留，我们优化后的模型就是只包含这几个效应的模型。利用原来的数据集对这个新的模型进行分析。因为因子B的影响非常小，所以它是high level还是low level没有显著区别，我们就可以把在因子B high level和low level下分别进行的两次试验看成是两次独立重复试验，这样$n$就等于2了，我们真正分析的试验变成了$2^3$试验。这时称多出来的这个replicate叫做hidden replicate。

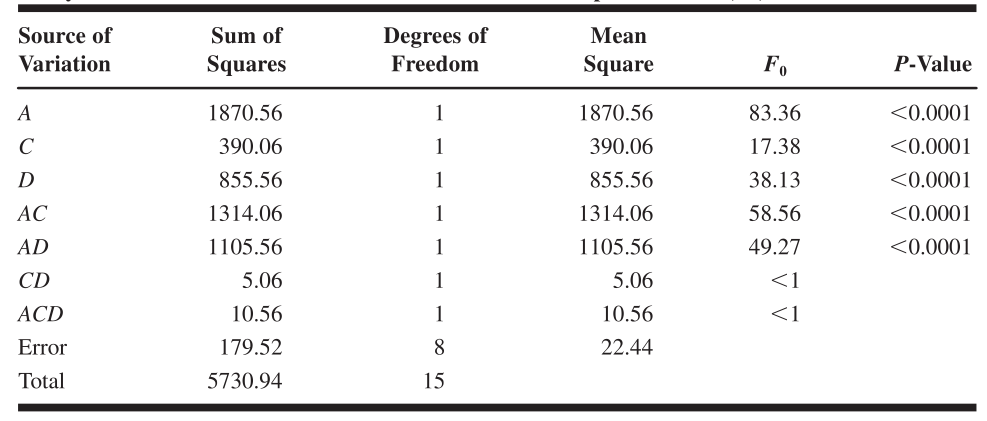
最后

以上就是会撒娇台灯为你收集整理的UA MATH571B 试验设计 2k析因设计理论上 2 k 2^k 2k析因设计Single-replicate 2 的全部内容，希望文章能够帮你解决UA MATH571B 试验设计 2k析因设计理论上 2 k 2^k 2k析因设计Single-replicate 2 所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。