概述
贝叶斯定理
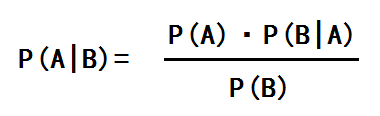
- P(A|B) 是在 B 发生的情况下 A 发生的概率；
- P(A) 是 A 发生的概率；
- P(B|A) 是在 A 发生的情况下 B 发生的概率；
- P(B) 是 B 发生的概率。
举个栗子说明，假设今天早上小明要出门，但是发现外面天空是多云状态，那么今天会不会下雨呢，或者说多云的情况下今天下雨的概率是多少呢？
- 事件A：今天下雨
- 事件B：早上有云
- 事件 A|B：早上有云，今天下雨
- 事件 B|A：今天下雨，早上有云
- P(A)：今天下雨的概率
- P(B)：早上有云的概率
- P(A|B)：早上有云的话，今天下雨的概率
- P(B|A)：今天下雨的话，早上有云的概率
小明现在要计算的是今天早上有云，今天下雨的概率是多少，即P(雨|云) = P(雨)·P(云|雨) / P(云)
假设：80% 的雨天早上是有云的，30% 的早上都是有云的，这几个月很干旱，平均每个月（30 天）下雨的天数是 6 天
那么P(雨|云) = 20% * 80% / 30% = 5.333%
因此，几乎可以认为今天不下雨。
贝叶斯定理一个著名的应用是假阳性和假阴性的检测。
再举个栗子：有一天小明收到一束花，过了一会突然感觉全身发痒，于是小天去做了个简单的过敏检测：
- 真的过敏的人，检测会给“有”的概率是 90%
- 没有过敏的人，检测给“有”的概率是5%，这被称为假阳性
现在已知的条件是小明所在的市区中有 1% 的人有这种过敏，而小明去检测得到的结果是“有”，那么小天真正过敏的概率是多少呢？
P(过敏|有) = P(过敏) · P(有|过敏) / P(有)
观察公式发现，P(有)不知道，即我们不知道检测得到结果是“有”的一般可能性是多少。考虑一下如何计算P(有)。
根据已知条件可以得到：
- 1% 的人是真的过敏的，得到“有”的概率是 90%
- 99% 的人是没有过敏的，得到“有”的概率是 5%
所以P(有) = P(过敏)·P(有|过敏) + P(不过敏)·P(有|不过敏) = 1% × 90% + 99% × 5% = 5.85%
最终，小明计算得到了他真正过敏的概率：
P(过敏|有) = 1% × 80% / 5.85% = 13.68%
这也是贝叶斯定理的特别版公式：
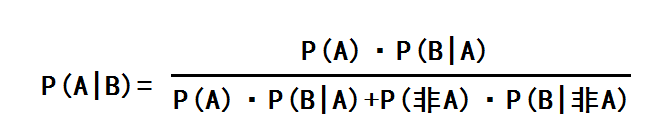
朴素贝叶斯定理也通常应用于人工智能领域，最常见的是朴素贝叶斯分类算法，也就是接下来要实现的基于概率的过滤器，本质上是通过计算概率来判断。
基于概率统计的过滤器
在充分了解贝叶斯定理后，再来看看，如何使用贝叶斯定理实现垃圾短信的过滤呢，即基于概率统计的过滤方式。
面对一条短信，我们通常可以通过这个短信的内容进行判断是否为垃圾短信。对于计算机来说无法直接通过内容来判断，但是我们可以将短信内容中的一些特征项提取出来，供计算机判断。
通过分词算法将短信内容分割成由n个单词的组合，那么现在的问题就变成了包含这些单词的短信是垃圾短信的概率是多少。
P(是垃圾短信 | 单词1、单词2 ... 单词 n 同时出现) = ?%
首先我们看一下理想状态该如何解这个概率，通过统计带有单词1、单词2、单词3同时出现的短信数量y和短信样本总数x，即可得到概率y/x。这个计算方法的问题在于，即便短信样本数量再大，也不会有太多是同时包含一系列单词的，极端情况可能根本没有。
现在我们使用朴素贝叶斯定理，来将这个概率转换成其他三个概率来求解：
P(是垃圾短信)的值很容易计算，样本中垃圾短信数与样本总数之比即可得到。
P(单词1、单词2 ... 单词 n 同时出现|是垃圾短信)的值不太好求，需要进行转换，首先我们来看一个公式：
独立事件发生的概率计算公式：P(A*B) = P(A)*P(B)
两个事件互为独立事件指的是这两个事件的发生没有相关性。
所以，P(单词1、单词2 ... 单词 n 同时出现|是垃圾短信)可以转换为如下公式：
最后，发现P(单词1、单词2 ... 单词 n 同时出现)的值也不太好求，前面说了由于样本数量有限，可能最终得到的值为 0。那么该如何解决呢？
其实我们没必要求这个分母，可以同时求包含这些单词的这条短信是垃圾短信和不是垃圾短信的概率，假设是垃圾短信的概率是p1，不是垃圾短信的概率是p2，这样一来，可以通过计算p1与p2的倍数关系来最终确定是否为垃圾短信，例如若p1是p2的十倍，那么可以认为短信一定是垃圾短信了。
拓展
在实际应用场景中，需要大量的实验，不断调整策略，并且需要权衡最终的准确率以及是否能把所有垃圾短信都找到。
最后
以上就是小巧纸鹤为你收集整理的朴素贝叶斯分类算法：垃圾短信的过滤原理的全部内容，希望文章能够帮你解决朴素贝叶斯分类算法：垃圾短信的过滤原理所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复