Python上的高等数学实验

1. 环境的建立

下载Python3, Download Python | Python.orghttps://www.python.org/downloads/

然后,安装需要的软件包, pandas, sympy,scipy,numpy, matplotlib, matplotlib.pyplot

pip install pandas

逐个安装, 把其中的包名称改一下即可

2. 为了方便显示, 再安装一个网页的界面 jupyter notebook

pip install jupyter

或者也可以安装 spider这个集成开发程序, 但是占用空间比较大, 界面和MATLAB类似

3. 进入界面.

在Win10系统下,键入Win+R, 打开命令行, 键入 

jupyter notebook

则系统会自动打开一个网页浏览器, 

 选择合适的文件夹, 点击右侧的"New", 下拉菜单中选择Python 3.

在新窗口的文本区输入命令, 点击"Run"执行命令, 结果将直接显示在输入命令的下面

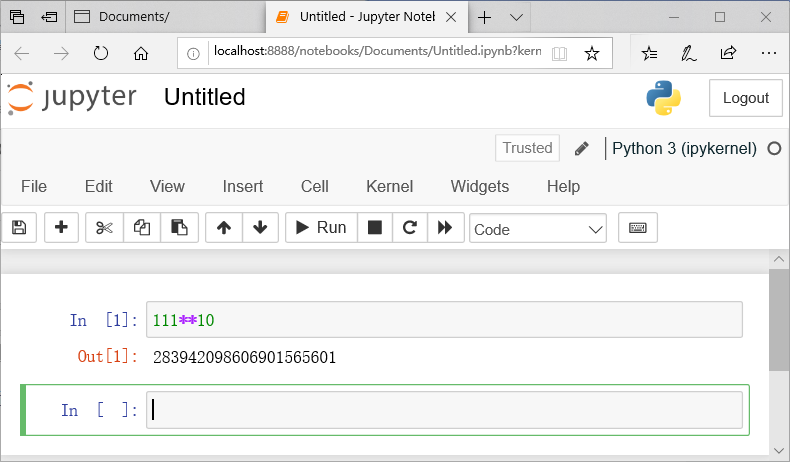
 其中的In[1]:之后就是输入的命令, **表示幂,这和其它语言比如C不一样. Out[1]则是指In[1]的输出结果, 这些输入和输出在后续的计算值都可以直接引用. 比如

Out[1]//12

这里的//表示整除,舍弃了余数.

至此, 需要的Python环境已经创建好了. 

注: 这个界面和Mathmatica何其相似啊!

第一部分 微积分学

1. 一元函数作图.

普通函数作图

import matplotlib.pyplot as plt
import math
x=[i/100 for i in range(1000)]
y=[math.sin(x) for x in x]
plt.plot(x,y)

分段函数

import matplotlib.pyplot as plt
import math
def f(x):
    if x>0: return math.sin(x)
    else: return math.cos(x)
xx=[i/100 for i in range(-100,100,1)]
yy=[f(x) for x in xx]
fig,ax=plt.subplots()
ax.plot(xx,yy)

2. 计算一元函数极限

from sympy import *
from sympy.abc import x,y
limit((1-cos(x))/x**2,x,0)

单侧极限

Limit命令默认计算右极限。 如果要求左极限，使用dir='-'参数。

from sympy.abc import x
limit(abs(x)/x,x,0,dir='-')
limit(abs(x)/x,x,0,dir='+')

当然要计算右极限时则把减号改成加号即可。

3. 计算导数

上述的符号计算包 sympy和sympy.abc只需要加载一次即可，后续命令中涉及新的变量时再添加， 前面已经加载的包，以及声明的符号变量则不再加载和声明。

diff(sin(x)/x,x)

计算高阶导数

diff(exp(x)*sin(x),x,3)

隐函数求导

y=Function('y')(x)
de=x*y
solve(diff(de),diff(y,x))

其中的de定义了隐函数等式左边不为零的部分，让后对x求导后，把y'通过解方程求解得到隐函数导数

4. 不定积分

integrate(sin(x**2)*x,x)

5. 定积分

integrate(exp(-x**2),(x,0,oo))

注：在Python中把无穷大用oo表示，而不是infty这个缩略词

6. 二次极限。 在Python和其它的计算软件中都没有计算重极限的命令，这里只能计算二次极限或者三次等累次极限，使用的就是嵌套的limit命令。

注意：当重极限和累次极限都存在的情况下它们才是相等的。

del y
from sympy.abc import y
limit(limit(sin(x*y)/x,x,0),y,1)

这里因为前面已经定义了y是x的隐函数，所以先删除以前的定义，然后重新定义其为符号变量，然后再嵌套两次使用limit求二次极限。

7. 偏导数

偏导数的计算和导数完全一致， 高阶偏导数的计算方法和高阶导数的类似

diff(sin(x*y),x,y)
diff(sin(x*y),x,2)
diff(sin(x*y),y,2)

8. 重积分

在计算软件中只能极限累次积分，需要手工把重积分先化成类似积分后才能用Python计算，命令依然是integrate.

integrate(x+y,(y,x**3,x**2),(x,0,1))

r,theta=symbols("r,theta")
integrate(2*r**3,(z,0,r**2),(r,0,2*cos(theta)),(theta,0,pi/2))

9. 曲线积分与曲面积分

和其他计算软件类似， Python也不能直接计算曲线积分和曲面积分， 需要手工把它们转换为定积分或者累次积分后，再使用integrate命令计算。

10. 无穷级数

因为计算机不可能进行无限次计算，所以不可能给出无限项。但是Python提供了函数展开的命令。

cos(x).series(x,n=10)

Python的Sympy包中内建函数中调用series方法可以得到函数的级数展开式，默认到x^6，当然也可以自己指定到x^n，其中的n是正整数。

计算数项级数的和

n=symbols("n",integer=True)
s=Sum((-1)**n/n**2,(n,1,oo))
s.doit()

这里先声明n是正整数，然后定义一个无穷和，最后计算。

求和函数

n=symbols("n",integer=True)
s=Sum(x**n/n,(n,1,oo))
s.doit()

这里的结果中不仅给出和函数，而且还附带给出收敛域。

对于Fourier级数可以直接计算系数，其中涉及到整数问题。先设定n是正整数，然后再计算。

n=symbols("n",integer=True,positive=True)
an=integrate(-x*cos(n*x),(x,-pi,0))/pi+integrate(x*cos(n*x),(x,0,pi))/pi
an

bn=integrate(-x*sin(n*x),(x,-pi,0))/pi+integrate(x*sin(n*x),(x,0,pi))/pi
bn

其中的结果会自动化简，不会出现cos(npi)这样奇葩的结果。

11. 常微分方程

y=Function("y")
ode=y(x).diff(x)-(1+y(x)**2)/(x*y(x)*(1+x))
#Eq(ode,0)
dsolve(ode)

 再看二阶微分方程，注意写方程时把右边清零，把左边部分定义为一个变量，再解方程

y=Function("y")
eqn=y(x).diff(x,2)-6*y(x).diff(x)+9*y(x)-exp(x)*cos(x)-x*sin(x)
Eq(eqn,0)
dsolve(eqn)

12. 二元函数作图

from mpl_toolkits.mplot3d.axes3d import Axes3D
import numpy as np
fig,ax=plt.subplots(1,1,subplot_kw={'projection':'3d'})
x=y=np.linspace(-3,3,74)
X,Y=np.meshgrid(x,y)
R=np.sqrt(X**2+Y**2)
Z=np.sin(4*R)/R
ax.plot_surface(X,Y,Z)

前两行先加载包，第三行的参数3d必不可少，因为后面的plot_surface命令依赖这个参数选择。x=y=np.linspace(-3,3,74)则是在两个坐标轴上选择点，X,Y=np.meshgrid(x,y)将两个坐标轴上选择的点变成网格数据，R=np.sqrt(X**2+Y**2)，Z=np.sin(4*R)/R则是计算因变量的值，最后一句就是作图命令。

最后

以上就是虚心咖啡豆为你收集整理的Python上的高等数学实验的全部内容，希望文章能够帮你解决Python上的高等数学实验所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。