python数学实验与建模第三章、第四章部分题解答

46 阅读 0 评论 31 点赞

我是靠谱客的博主动听香水，最近开发中收集的这篇文章主要介绍python数学实验与建模第三章、第四章部分题解答，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

3.6求解下列线性方程组

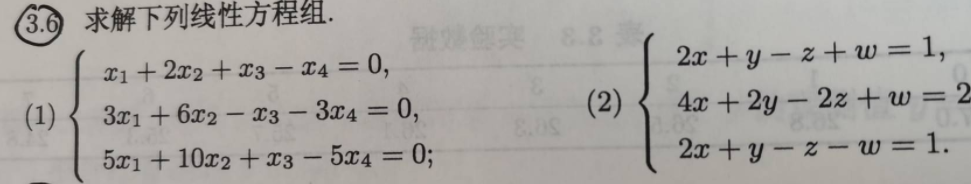
在这里插入图片描述

import sympy as sp
A = sp.Matrix([[1,2,1,-1], [3,6,-1,-3], [5,10,1,-5]])
result = A.nullspace()
print("A的通解为: ", result)

import sympy as sp
A = sp.Matrix([[2,1,-1,1],[4,2,-2,1],[2,1,-1,-1]])
b = sp.Matrix([1,2,1])
b.transpose()  #转置矩阵
C = A.row_join(b) #构造增广矩阵
print("增广矩阵的行最简形为：n", C.rref())

3.7先判断下列线性方程组解的情况，然后求对应的唯一解、最小二乘解或最小范数解

在这里插入图片描述

import numpy as np
import numpy.linalg as la
from numpy.linalg import pinv
A = np.array([[4,2,-1],[3,-1,2],[11,3,0]])
b = np.array([[2,10,8]])
b = b.reshape(3,1)  #转置
print("矩阵A的秩为:", la.matrix_rank(A))
print("最小范数解为：n", pinv(A).dot(b)) #求最小范数解

import numpy as np
from numpy.linalg import pinv
import numpy.linalg as la
A = np.array([[2,3,1],[1,-2,4],[3,8,-2],[4,-1,9]])
b = np.array([4,-5,13,-6])
b = b.reshape(4,1) #b的转置
result = pinv(A).dot(b)
print("矩阵A的秩为:", la.matrix_rank(A))
print("线性方程组的解为：", result)

4.4表4.20列出了某一地区在夏季的一个月中由100个气象站报告的雷暴雨的次数，试用卡方拟合检验法检验雷暴雨的次数X是否服从均值为1的泊松分布

在这里插入图片描述

import numpy as np
import pandas as pd
from scipy import stats
from scipy.stats.stats import Power_divergenceResult
d = {'x': range(0,6), 'y':[22, 37, 20, 13, 6, 2]}
df = pd.DataFrame(d)
Poiss=stats.poisson(mu=1)
df['prop']=Poiss.pmf(df['x'])
df['t_days']=100*df['prop']
print(df)
df1=pd.DataFrame(df)
n=None
for i in range(len(df1)):
    if df1.iloc[i,3] < 5:
        n =i
        df1.iloc[i+1,:] = df1.iloc[i+1,:] + df1.iloc[i,:]
    else:
        break
if n is not None:
    df1 = df1.iloc[n+1:,:]
result = stats.chisquare(df1['y'], df1['t_days'], ddof=1)
print(result)
print("pvalue < 0.05 所以不满足均值为1的泊松分布")

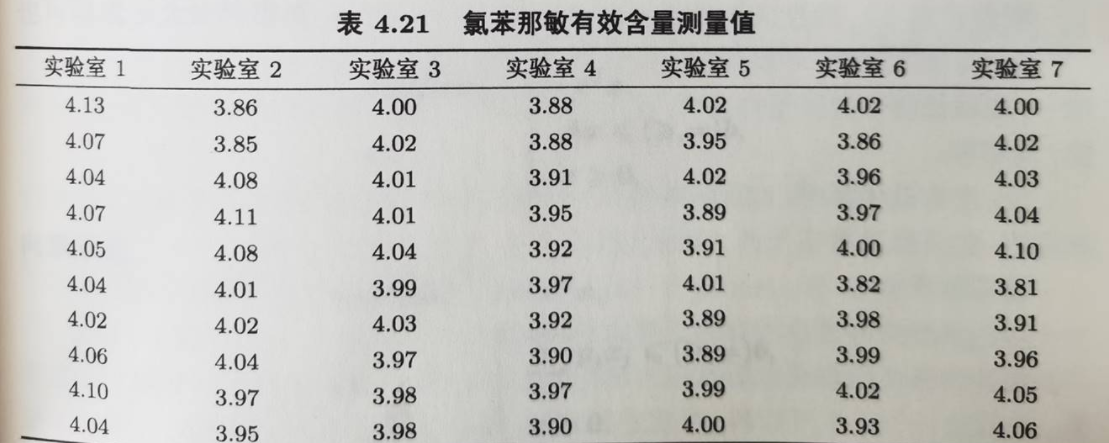
4.6在7个不同实验室中测量某种氯苯那敏药片的氯苯那敏有效含量，得到结果如表所列，试做单因素方差分析

在这里插入图片描述

import numpy as np
import statsmodels.api as sm
import csv
import pandas as pd
y = np.array([1.13,1.07,4.04,4.07,4.05,4.04,4.02,4.06,4.10,4.04,
              3.86,3.85,4.08,4.11,4.08,4.01,4.02,4.04,3.97,3.95,
              4.00,4.02,4.01,4.01,4.04,3.99,4.03,3.97,3.98,3.98,
              3.88,3.88,3.91,3.95,3.92,3.97,3.92,3.90,3.97,3.90,
              4.02,3.95,4.02,3.89,3.91,4.01,3.89,3.89,3.99,4.00,
              4.02,3.86,3.96,3.97,4.00,3.82,3.98,3.99,4.02,3.93,
              4.00,4.02,4.03,4.04,4.10,3.81,3.91,3.96,4.05,4.06
              ])
x=np.hstack([np.full(10,1), np.full(10,2), np.full(10,3),
             np.full(10,4), np.full(10,5), np.full(10,6), np.full(10,7)])
d = {'x':x, 'y':y} #构造字典
model = sm.formula.ols("y~C(x)", d).fit() #构建模型
anovat = sm.stats.anova_lm(model)
print(anovat)

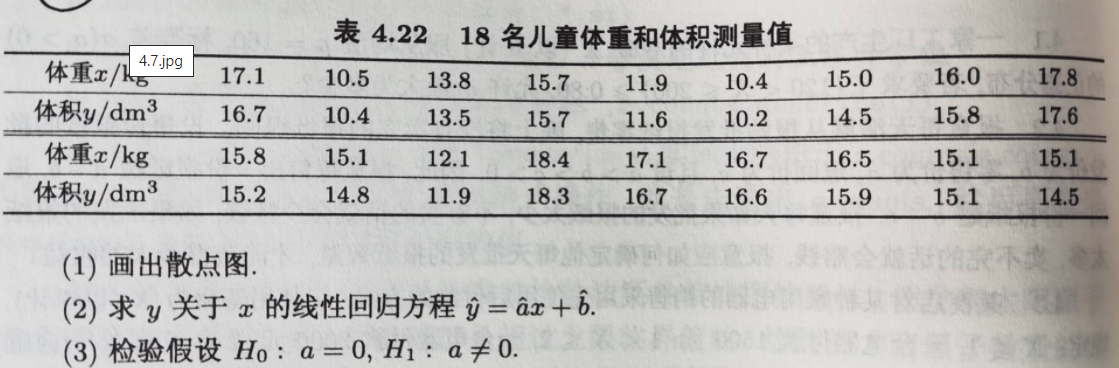
4.7表4.22列出了18名5-8岁儿童的体重和体积测量值，试画出散点图、线性回归方程、假设检验
在这里插入图片描述

import matplotlib.pylab as plt
import numpy as np
from statsmodels.formula.api import ols
x = [17.1,10.5,13.8,15.7,11.9,10.4,15.0,16.0,17.8,
     15.8,15.1,12.1,18.4,17.1,16.7,16.5,15.1,15.1]
y = [16.7,10.4,13.5,15.7,11.6,10.2,14.5,15.8,17.6,
     15.2,14.8,11.9,18.9,16.7,16.6,15.9,15.1,14.5]
plt.plot(x, y, '+k', label = "原始数据点")
p = np.polyfit(x, y, deg=1)  #拟合一次多项式
print("拟合的多项式为:{}*x + {}".format(p[0], p[1]))
plt.rc('font', size = 16);
plt.rc('font', family = 'SimHei')
plt.plot(x, np.polyval(p,x), 'g-', label = "拟合的直线")
plt.legend() #显示多个标签
plt.show()
#显著性检测 方法一,利用ols
data = {'x':x, 'y':y}
model = ols('y~x', data).fit()
print(model.summary())
#显著性检测 方法二，手推公式
mean_x = np.mean(x)
mean_y = np.mean(y)
num1 = num2 = num3 = 0
for i in range(0, 18):
    num1 = num1 + x[i]*y[i]
    num2 = num2 + y[i]**2
    num3 = num3 + y[i]
result1 = p[0]*(num1 - 18*mean_x*mean_y)
result2 = num2 - p[1]*num3 - p[0]*num1
F = result1 / (result2 / 16)
print("假设检验结果为：",F)
if(F > 5.32):
    print("落在拒绝域，所以X与Y的线性方程是显著的")