第3章 Python在高等数学和线性代数中的应用
- SymPy工具介绍
- SciPy工具库简介
- 用SymPy做符号函数画图
- 高等数学问题的符号解
- 高等数学问题的数值解
- 线性代数问题的符号解和数值解
1.SymPy工具库介绍
1)sympy工具库简介
SymPy是Python版的开源计算机代数系统实现,通俗地讲,SymPy是用于符号运算的工具库,现在这个工具库包括几十个模块:
>>> help('sympy')
Help on package sympy:
NAME
sympy
DESCRIPTION
SymPy is a Python library for symbolic mathematics. It aims to become a
full-featured computer algebra system (CAS) while keeping the code as simple
as possible in order to be comprehensible and easily extensible. SymPy is
written entirely in Python. It depends on mpmath, and other external librari
es
may be optionally for things like plotting support.
See the webpage for more information and documentation:
https://sympy.org
PACKAGE CONTENTS
abc # 符号变量模块
algebras (package) # 代数
assumptions (package)
benchmarks (package)
calculus (package)
categories (package)
codegen (package)
combinatorics (package)
concrete (package)
conftest
core (package) # 基本的加、乘、指数运算等
crypto (package)
deprecated (package)
diffgeom (package)
discrete (package) # 离散数学
external (package)
functions (package)
galgebra # 几何代数
geometry (package) # 几何实体
holonomic (package)
integrals (package) # 符号积分
interactive (package) # 交互会话
liealgebras (package)
logic (package) # 布尔代数和定理证明
matrices (package) # 线性代数和矩阵
multipledispatch (package)
ntheory (package) # 数论函数
parsing (package)
physics (package) # 物理学
plotting (package) # 用Pyglet进行二维和三维的画图
polys (package) # 多项式代数和因式分解
printing (package) # 漂亮的打印和代码生成
release
sandbox (package)
series (package) # 级数
sets (package)
simplify (package) # 化简符号表达式
solvers (package) # 方程求解
stats (package) # 统计学
strategies (package)
tensor (package)
testing (package)
this
unify (package)
utilities (package)
vector (package)详细资料:
SymPy Modules Reference Python科学计算利器——SymPy库
几个模块的功能:
- 微积分模块(sympy.intergrals):微积分模块支持大量的基础与高级微积分运算功能。
- 离散数学模块(sympy.discrete)
- 方程求解模块(sympy.solvers)
- 矩阵模块(sympy.matrices)
- 物理学模块(sympy.physics)
- 统计学模块(sympy.stats)
2)符号运算基础知识
符号创建、类型转换及subs()方法代入值示例:
from sympy import *
x, y, z = symbols('x y z')
m0, m1, m2, m3 = symbols('m0:4') # 创建多个符号变量
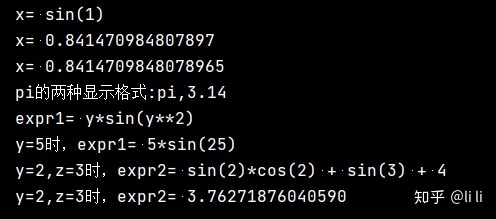
x = sin(1)
print("x=", x);
print("x=", x.evalf())
print("x=", x.n(16)) # 显示小数点后16位数字
print("pi的两种显示格式:{},{}".format(pi, pi.evalf(3))) # 这里不能使用n()函数
expr1 = y * sin(y ** 2) # 创建第一个符号表达式
expr2 = y ** 2 + sin(y) * cos(y) + sin(z) # 创建第二个符号表达式
print("expr1=", expr1)
print("y=5时,expr1=", expr1.subs(y, 5)) # 代入一个符号变量的值
print("y=2,z=3时,expr2=", expr2.subs({y: 2, z: 3})) # 代入y=2,z=3
print("y=2,z=3时,expr2=", expr2.subs({y: 2, z: 3}).n()) # 以浮点数显示计算结果运行结果:
符号函数together()及apart()使用示例:
from sympy import *
x1, x2, x3, x4 = symbols('m1:5')
x = symbols('x')
print(x1 / x2 + x3 / x4)
print(together(x1 / x2 + x3 / x4))
print((2 * x ** 2 + 3 * x + 4) / (x + 1))
print(simplify((2 * x ** 2 + 3 * x + 4) / (x + 1))) # 化简没有效果
print(apart((2 * x ** 2 + 3 * x + 4) / (x + 1)))运行结果:
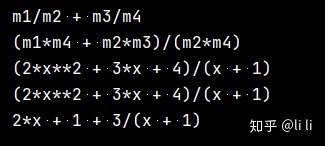
2.SciPy工具库简介
SciPy是对NumPy的功能扩展,它提供了许多高级数学函数,例如,微积分、微分方程、优化方法、数值分析、高级统计函数、方程求解等。SciPy是在NumPy数组框架基础上实现的,它对NumPy数组和基本的数组运算进行扩展,满足科学家和工程师解决问题时需要的大部分数学计算功能。
详细资料:SciPy v1.6.0 Reference Guide

SciPy可以使用MATLAB的“.mat”文件格式读取和写入数据,函数为loadmat和savemat。
3.用SymPy做符号函数画图
1)二维曲线画图
plot的基本使用格式:
plot(表达式, 变量取值范围, 属性 = 属性值)多重绘制的使用格式为:
plot(表达式1, 表达式2, 变量取值范围, 属性 = 属性值)或者:
plot((表达式1, 变量取值范围1), (表达式2, 变量取值范围2))例:在同一图形界面上画出
from sympy.plotting import plot
from sympy.abc import x, pi # 引进符号变量x及常量pi
from sympy.functions import sin, cos
plot((2 * sin(x), (x, -6, 6)), (cos(x + pi / 4), (x, -5, 5)))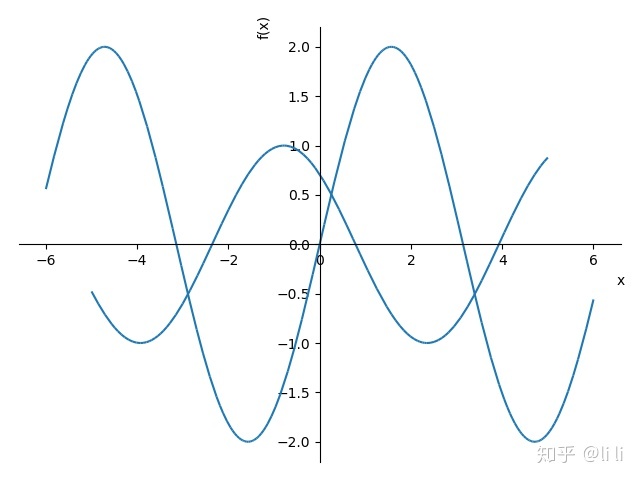
2)三维曲面画图
例:画出三维曲面
from pylab import rc # pylab为matplotlib的接口
from sympy.plotting import plot3d
from sympy.abc import x, y # 引进符号变量x,y
from sympy.functions import sin, sqrt
rc('font', size=16);
rc('text', usetex=True)
plot3d(sin(sqrt(x ** 2 + y ** 2)), (x, -10, 10), (y, -10, 10), xlabel='$x$', ylabel='$y$')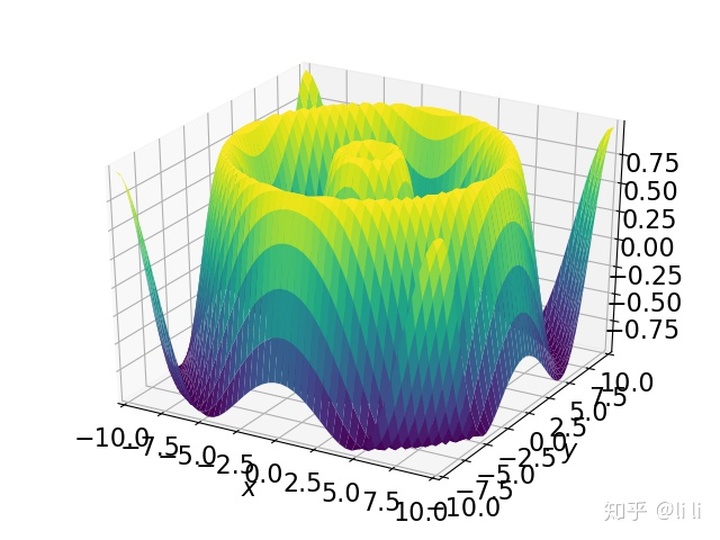
3)隐函数画图
例:绘制隐函数
from pylab import rc
from sympy import plot_implicit as pt, Eq
from sympy.abc import x, y # 引进符号变量x,y
rc('font', size=16)
rc('text', usetex=False)
pt(Eq((x - 1) ** 2 + (y - 2) ** 3, 4), (x, -6, 6), (y, -2, 4), xlabel='$x$', ylabel='$y$')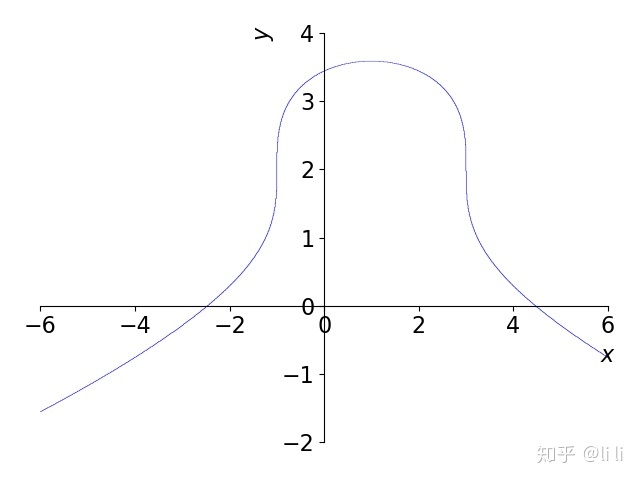
或使用以下代码:
from sympy import plot_implicit as pt
from sympy.abc import x, y # 引进符号变量x,y
ezplot = lambda expr: pt(expr)
ezplot((x - 1) ** 2 + (y - 2) ** 3 - 4)4.高等数学问题的符号解
SymPy包括许多功能,从基本的符号算术到多项式、微积分、求解方程、离散数学和统计等。它主要处理三种类型的数据:整型数据、实数和有理数。有理数包括两个部分:分子和分母,可以用Ration类定义有理数。
1)求极限
例:验证
from sympy import *
x = symbols('x')
print(limit(sin(x) / x, x, 0))
print(limit(pow(1 + 1 / x, x), x, oo)) # 这里是两个小”o”,表示正无穷运行结果:

2)求导数
例:已知
from sympy import *
x, y = symbols('x y') # 定义两个符号变量
z = sin(x) + x ** 2 * exp(y) # 构造符号表达式
print("关于x的二阶偏导数为:", diff(z, x, 2))
print("关于y的一阶偏导数为:", diff(z, y))运行结果:
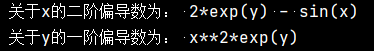
3)级数求和
例:验证
from sympy import *
k, n = symbols('k n')
print(summation(k ** 2, (k, 1, n)))
print(factor(summation(k ** 2, (k, 1, n)))) # 把计算结果因式分解
print(summation(1 / k ** 2, (k, 1, oo))) # 这里是两个小o表示正无穷运行结果:
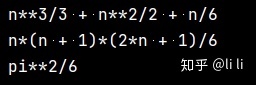
4)泰勒展开
例:写出
from pylab import rc
from sympy import *
rc('font', size=16)
rc('text', usetex=False)
x = symbols('x')
y = sin(x)
for k in range(3, 8, 2):
print(y.series(x, 0, k)) # 等价于print(series(y,x,0,k))
plot(y, series(y, x, 0, 3).removeO(), series(y, x, 0, 5).removeO(),
series(y, x, 0, 7).removeO(), (x, 0, 2), xlabel='$x$', ylabel='$y$')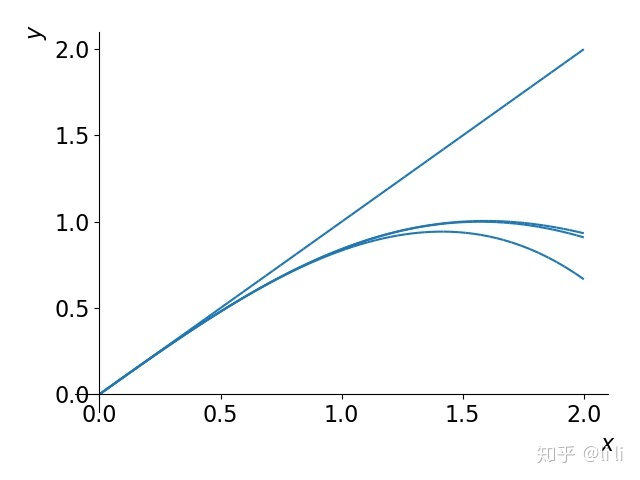
5)不定积分和定积分
例:验证
from sympy import integrate, symbols, sin, pi, oo
x = symbols('x')
print(integrate(sin(2 * x), (x, 0, pi)))
print(integrate(sin(x) / x, (x, 0, oo)))运行结果:

6)求解代数方程(方程组)的符号解
例:求如下代数方程:(1)
from sympy import *
x, y = symbols('x y')
print(solve(x ** 3 - 1, x))
print(solve((x - 2) ** 2 * (x - 1) ** 3, x))
print(roots((x - 2) ** 2 * (x - 1) ** 3, x)) # roots可以得到根的重数信息运行结果:

例:求解如下代数方程组
from sympy.abc import x, y
from sympy import solve
s = solve([x ** 2 + y ** 2 - 1, x - y], [x, y])
print("方程组的解为:", s)运行结果:

例:求函数
驻点:函数的一阶导数为0的点(驻点也称为稳定点,临界点)。对于多元函数,驻点是所有一阶偏导数都为零的点。驻点(数学概念)_百度百科
from sympy import *
x = symbols('x')
y = 2 * x ** 3 - 5 * x ** 2 + x
x0 = solve(diff(y, x), x) # 求驻点
print("驻点的精确解为", x0)
print("驻点的浮点数表示为:", [x0[i].n() for i in range(len(x0))]) # 列表中的符号数无法整体转换为浮点数
y0 = [y.subs(x, 0), y.subs(x, 1), y.subs(x, x0[0]).n()] # 代入区间端点和一个驻点的值
print("三个点的函数值分别为:", y0)运行结果:

7)求微分方程(方程组)的符号解
例:求下列微分方程的通解:
(1)齐次方程:
(2)非齐次方程:
from sympy import *
x = symbols('x')
y = symbols('y', cls=Function)
eq1 = diff(y(x), x, 2) - 5 * diff(y(x), x) + 6 * y(x)
eq2 = diff(y(x), x, 2) - 5 * diff(y(x), x) + 6 * y(x) - x * exp(2 * x)
print("齐次方程的解为:", dsolve(eq1, y(x)))
print("非齐次方程的解为:", dsolve(eq2, y(x)))运行结果:

例:求下列微分方程的解:
(1)初值问题:
(2)边值问题:
from sympy import *
x = symbols('x');
y = symbols('y', cls=Function)
eq1 = diff(y(x), x, 2) - 5 * diff(y(x), x) + 6 * y(x)
eq2 = diff(y(x), x, 2) - 5 * diff(y(x), x) + 6 * y(x) - x * exp(2 * x)
print("初值问题的解为:{}".format(dsolve(eq1, y(x), ics={y(0): 1, diff(y(x), x).subs(x, 0): 0})))
y2 = dsolve(eq2, y(x), ics={y(0): 1, y(2): 0})
print("边值问题的解为:{}".format(y2))运行结果:

5.高等数学问题的数值解
大多数实际问题是无法求符号解的,只能求数值解,即近似解。
1)泰勒级数与数值导数
泰勒级数:
例:画出
编写如下函数mysin求
import numpy as np
import matplotlib.pyplot as plt
def fac(n):
return 1 if n < 1 else n * fac(n - 1)
def item(n, x):
return (-1) ** n * x ** (2 * n + 1) / fac(2 * n + 1)
def mysin(n, x):
return 0 if n < 0 else mysin(n - 1, x) + item(n, x)
x = np.linspace(-2 * np.pi, 2 * np.pi, 101)
plt.plot(x, np.sin(x), '*-')
str = ['v-', 'H--', '-.']
for n in [1, 2, 3]: plt.plot(x, mysin(2 * n - 1, x), str[n - 1])
plt.legend(['sin', 'n=1', 'n=3', 'n=5'])
plt.savefig('figure3_16.png', dpi=500)
plt.show()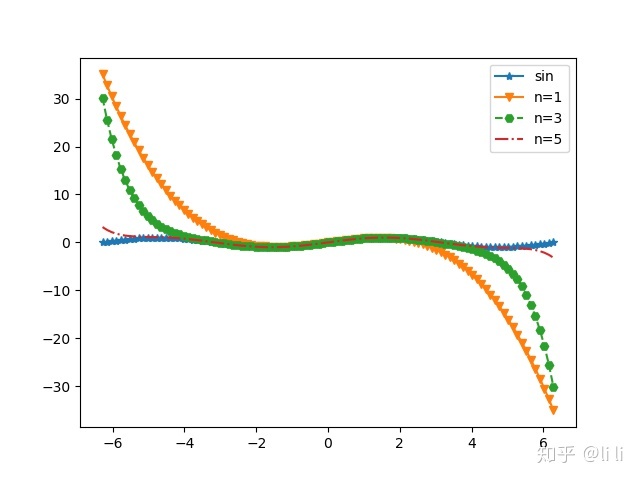
数值导数:
利用泰勒级数可以给出近似计算函数导数的方法.例如,若
这是一个常用的用于估计函数一阶导数的计算公式,它具有一阶精度.此外,还可以推出具有二阶精度的估计公式:
当函数具有更高阶的导数时,如利用
以及
可得二阶导数计算公式:
例:甲、乙、丙、丁4个人分别位于起始位置(-200,200),(200,200),(200,-200),(-200,-200)处(单位:米),并且以恒定的速率1m/s行走,在行走过程中,甲始终朝向乙的当前位置;同样,乙朝向丙、丙朝向丁、丁朝向甲.试绘制4人行走过程的近似轨迹。
import numpy as np, numpy.linalg as ng
import matplotlib.pyplot as plt
N = 4
v = 1.0
d = 200.0
time = 400.0
divs = 201
xy = np.array([[-d, d], [d, d], [d, -d], [-d, -d]])
T = np.linspace(0, time, divs)
dt = T[1] - T[0]
xyn = np.empty((4, 2))
Txy = xy
for n in range(1, len(T)):
for i in [0, 1, 2, 3]:
j = (i + 1) % 4
dxy = xy[j] - xy[i]
dd = dxy / ng.norm(dxy) # 单位化向量
xyn[i] = xy[i] + v * dt * dd # 计算下一步的位置
Txy = np.c_[Txy, xyn]
xy = xyn
for i in range(N):
plt.plot(Txy[i, ::2], Txy[i, 1::2])
plt.savefig("figure3_17.png", dpi=500)
plt.show()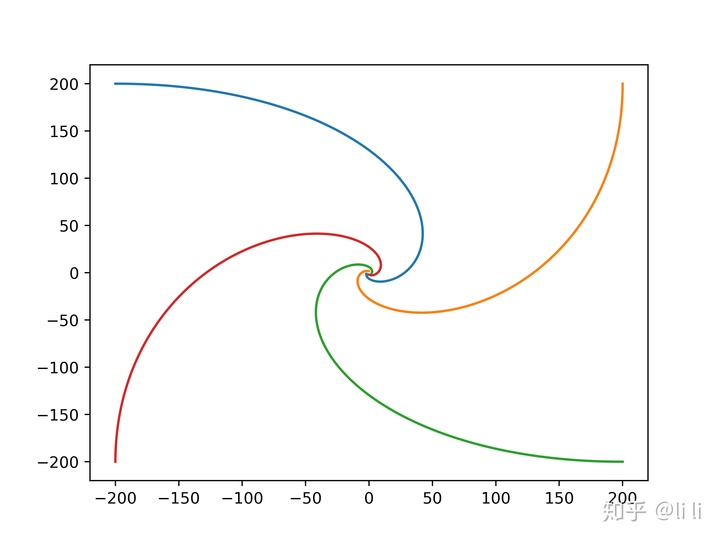
2)数值积分
分别使用梯形公式、辛普森公式和SciPy工具库中的函数quad求定积分
import numpy as np
from scipy.integrate import quad
def trapezoid(f, n, a, b): # 定义梯形公式的函数
xi = np.linspace(a, b, n)
h = (b - a) / (n - 1)
return h * (np.sum(f(xi)) - (f(a) + f(b)) / 2)
def simpson(f, n, a, b): # 定义辛普森公式的函数
xi, h = np.linspace(a, b, 2 * n + 1), (b - a) / (2.0 * n)
xe = [f(xi[i]) for i in range(len(xi)) if i % 2 == 0]
xo = [f(xi[i]) for i in range(len(xi)) if i % 2 != 0]
return h * (2 * np.sum(xe) + 4 * np.sum(xo) - f(a) - f(b)) / 3.0
a = 0
b = 1
n = 1000
f = lambda x: np.sin(np.sqrt(np.cos(x) + x ** 2))
print("梯形积分I1=", trapezoid(f, n, a, b))
print("辛普森积分I2=", simpson(f, n, a, b))
print("SciPy积分I3=", quad(f, a, b))运算结果:

例:分别求下列积分的数值解.
(1)
对于(2)中的二重积分,先要化成累次积分
import numpy as np
from scipy.integrate import dblquad
f1 = lambda y, x: x * y ** 2 # 第一个被积函数
print("I1:", dblquad(f1, 0, 2, 0, 1))
f2 = lambda y, x: np.exp(-x ** 2 / 2) * np.sin(x ** 2 + y)
bd = lambda x: np.sqrt(1 - x ** 2)
print("I2:", dblquad(f2, -1, 1, lambda x: -bd(x), bd))运行结果:

例:计算
先把三重积分化成累次积分
import numpy as np
from scipy.integrate import tplquad
f = lambda z, y, x: z * np.sqrt(x ** 2 + y ** 2 + 1)
ybd = lambda x: np.sqrt(2 * x - x ** 2)
print("I=", tplquad(f, 0, 2, lambda x: -ybd(x), ybd, 0, 6))运行结果:

3)非线性方程(组)数值解
例:求方程
import numpy as np
from scipy.optimize import fsolve
def binary_search(f, eps, a, b): # 二分法函数
c = (a + b) / 2
while np.abs(f(c)) > eps:
if f(a) * f(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
return c
def newton_iter(f, eps, x0, dx=1E-8): # 牛顿迭代法函数
def diff(f, dx=dx): # 求数值导数函数
return lambda x: (f(x + dx) - f(x - dx)) / (2 * dx)
df = diff(f, dx)
x1 = x0 - f(x0) / df(x0)
while np.abs(x1 - x0) >= eps:
x1, x0 = x1 - f(x1) / df(x1), x1
return x1
f = lambda x: x ** 3 + 1.1 * x ** 2 + 0.9 * x - 1.4
print("二分法求得的根为:", binary_search(f, 1E-6, 0, 1))
print("牛顿迭代法求得的根为:", newton_iter(f, 1E-6, 0))
print("直接调用SciPy求得的根为:", fsolve(f, 0))运行结果:
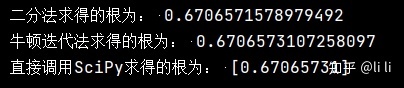
用fsolve求非线性方程组的数值 解
例:求下列非线性方程组的数值解.
from numpy import sin
from scipy.optimize import fsolve
f = lambda x: [5 * x[1] + 3, 4 * x[0] ** 2 - 2 * sin(x[1] * x[2]), x[1] * x[2] - 1.5]
print("result=", fsolve(f, [1.0, 1.0, 1.0]))运行结果:

或:
from numpy import sin
from scipy.optimize import fsolve
def Pfun(x):
x1, x2, x3 = x.tolist() # x转换成列表
return 5 * x2 + 3, 4 * x1 ** 2 - 2 * sin(x2 * x3), x2 * x3 - 1.5
print("result=", fsolve(Pfun, [1.0, 1.0, 1.0]))4)函数极值点的数值解
求函数
from numpy import exp, cos
from scipy.optimize import fminbound
f = lambda x: exp(x) * cos(2 * x)
x0 = fminbound(f, 0, 3)
print("极小点为:{},极小值为:{}".format(x0, f(x0)))运行结果:

求函数
from numpy import exp, cos
from scipy.optimize import fmin
f = lambda x: exp(x) * cos(2 * x)
x0 = fmin(f, 0)
print("极小点为:{},极小值为:{}".format(x0, f(x0)))运行结果:
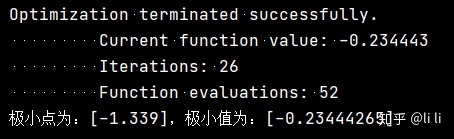
多元函数的极值点:
求函数
from scipy.optimize import minimize
f = lambda x: 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
x0 = minimize(f, [2.0, 2.0]) # [2.0, 2.0]为初始猜测值
print("极小点为:{},极小值为:{}".format(x0.x, x0.fun))运行结果:

6.线性代数问题的符号解和数值解
1)线性代数问题的符号解
矩阵的运算
已知
例:已知
import sympy as sp
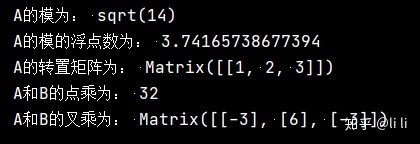
A = sp.Matrix([[1], [2], [3]]) # 列向量,即3×1矩阵
B = sp.Matrix([[4], [5], [6]])
print("A的模为:", A.norm())
print("A的模的浮点数为:", A.norm().evalf())
print("A的转置矩阵为:", A.T)
print("A和B的点乘为:", A.dot(B))
print("A和B的叉乘为:", A.cross(B))运行结果:
例:已知
import sympy as sp
import numpy as np
A = sp.Matrix(np.arange(1, 17).reshape(4, 4))
B = sp.eye(4)
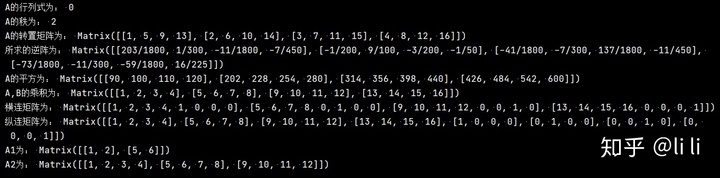
print("A的行列式为:", sp.det(A))
print("A的秩为:", A.rank())
print("A的转置矩阵为:", A.transpose()) # 等价于A.T
print("所求的逆阵为:", (A + 10 * B).inv())
print("A的平方为:", A ** 2)
print("A,B的乘积为:", A * B)
print("横连矩阵为:", A.row_join(B))
print("纵连矩阵为:", A.col_join(B))
print("A1为:", A[0:2, 0:2])
A2 = A.copy()
A2.row_del(3)
print("A2为:", A2)运行结果:
解线性方程组:
例:求下列线性方程组的符号解.
解 记上述线性方程组为
import sympy as sp
A = sp.Matrix([[2, 1, -5, 1], [1, -3, 0, -6], [0, 2, -1, 2], [1, 4, -7, 6]])
b = sp.Matrix([8, 6, -2, 2]);
b.transpose()
print("系数矩阵A的秩为:", A.rank())
print("线性方程组的唯一解为:", A.inv() * b)运行结果:

例:求下列齐次线性方程组的基础解系.
import sympy as sp
A = sp.Matrix([[1, -5, 2, -3], [5, 3, 6, -1], [2, 4, 2, 1]])
print("A的零空间(即基础解系)为:", A.nullspace())运行结果:
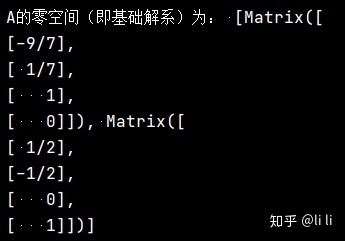
即求得的基础解系为:
例:求下列非齐次线性方程组的通解.
求通解要先使用rref()方法把增广矩阵化为行最简.
import sympy as sp
A = sp.Matrix([[1, 1, -3, -1], [3, -1, -3, 4], [1, 5, -9, -8]])
b = sp.Matrix([1, 4, 0])
b.transpose()
C = A.row_join(b) # 构造增广矩阵
print("增广阵的行最简形为:n", C.rref())运行结果:
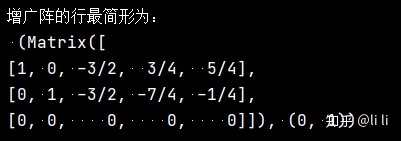
通过行最简可以写出原方程组的等价方程组为
所以方程组的通解为
例:求下列矩阵的特征值和特征向量.
import sympy as sp
A = sp.Matrix([[0, -2, 2], [-2, -3, 4], [2, 4, -3]])
print("A的特征值为:", A.eigenvals())
print("A的特征向量为:", A.eigenvects())运行结果:
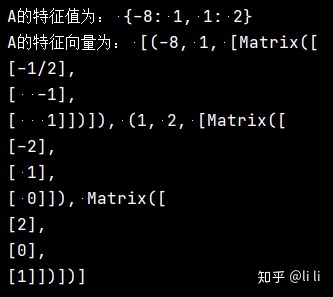
求得的特征值为
对应于特征值1的两个线性无关 的特征向量为
例:把下列矩阵相似对角化,即求可逆矩阵P,使得
from sympy import Matrix, diag
A = Matrix([[0, -2, 2], [-2, -3, 4], [2, 4, -3]])
if A.is_diagonalizable():
print("A的对角化矩阵为:", A.diagonalize())
else:
print("A不能对角化")运行结果:
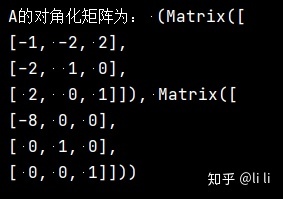
求得的可逆矩阵P和对角阵D分别为
2)线性代数问题的数值解
向量和矩阵的运算:
例:已知
from numpy import arange, cross, inner
from numpy.linalg import norm
a = arange(1, 4);
b = arange(4, 7) # 创建数组
print("a的二范数为:", norm(a))
print("a点乘b=", a.dot(b)) # 行向量a乘以列向量b
print("a,b的内积=", inner(a, b)) # a,b的内积,这里与dot(a,b)等价
print("a叉乘b=", cross(a, b))运行结果:
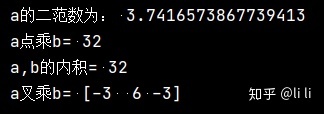
例:已知
import numpy as np
import numpy.linalg as LA
A = np.arange(1, 17).reshape(4, 4)
B = np.eye(4)
print("A的行列式为:", LA.det(A))
print("A的秩为:", LA.matrix_rank(A))
print("A的转置矩阵为:n", A.transpose()) # 等价于A.T
print("所求的逆阵为:n", LA.inv(A + 10 * B))
print("A的平方为:n", A.dot(A))
print("A,B的乘积为:n", A.dot(B))
print("横连矩阵为:", np.c_[A, B])
print("纵连矩阵为:", np.r_[A, B])
print("A1为:", A[0:2, 0:2])
A2 = A.copy();
A2 = np.delete(A2, 3, axis=0)
print("A2为:", A2)运行结果:
A的行列式为: 4.7331654313261276e-30
A的秩为: 2
A的转置矩阵为:
[[ 1 5 9 13]
[ 2 6 10 14]
[ 3 7 11 15]
[ 4 8 12 16]]
所求的逆阵为:
[[ 0.11277778 0.00333333 -0.00611111 -0.01555556]
[-0.005 0.09 -0.015 -0.02 ]
[-0.02277778 -0.02333333 0.07611111 -0.02444444]
[-0.04055556 -0.03666667 -0.03277778 0.07111111]]
A的平方为:
[[ 90 100 110 120]
[202 228 254 280]
[314 356 398 440]
[426 484 542 600]]
A,B的乘积为:
[[ 1. 2. 3. 4.]
[ 5. 6. 7. 8.]
[ 9. 10. 11. 12.]
[13. 14. 15. 16.]]
横连矩阵为: [[ 1. 2. 3. 4. 1. 0. 0. 0.]
[ 5. 6. 7. 8. 0. 1. 0. 0.]
[ 9. 10. 11. 12. 0. 0. 1. 0.]
[13. 14. 15. 16. 0. 0. 0. 1.]]
纵连矩阵为: [[ 1. 2. 3. 4.]
[ 5. 6. 7. 8.]
[ 9. 10. 11. 12.]
[13. 14. 15. 16.]
[ 1. 0. 0. 0.]
[ 0. 1. 0. 0.]
[ 0. 0. 1. 0.]
[ 0. 0. 0. 1.]]
A1为: [[1 2]
[5 6]]
A2为: [[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]齐次方程的数值解:
例:求下列齐次线性方程组的基础解系.
import numpy as np
from scipy.linalg import null_space
A = np.array([[1, -5, 2, -3], [5, 3, 6, -1], [2, 4, 2, 1]])
print("A的零空间(即基础解系)为:", null_space(A))运行结果:
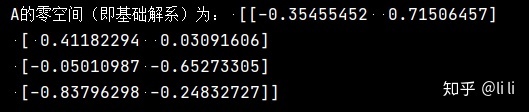
非齐次线性方程组的数值解:
例:求下列线性方程组的数值解.
解 记上述线性方程组为
import numpy as np
import numpy.linalg as LA
A = np.array([[2, 1, -5, 1], [1, -3, 0, -6], [0, 2, -1, 2], [1, 4, -7, 6]])
b = np.array([[8, 6, -2, 2]]);
b = b.reshape(4, 1)
print("系数矩阵A的秩为:", LA.matrix_rank(A))
print("线性方程组的唯一解为:", LA.inv(A).dot(b)) # 使用逆矩阵
print("线性方程组的唯一解为:", LA.pinv(A).dot(b)) # 使用伪逆
print("线性方程组的唯一解为:", LA.solve(A, b)) # 利用solve求解运行结果:
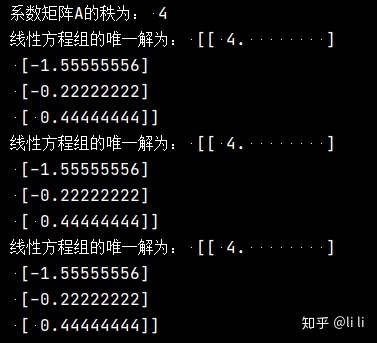
例:下列非齐次线性方程组有无穷多解,求它的最小范数解.
from numpy import array
from numpy.linalg import pinv
A = array([[1, 1, -3, -1], [3, -1, -3, 4], [1, 5, -9, -8]])
b = array([1, 4, 0])
b.resize(3, 1)
x = pinv(A).dot(b) # 求最小范数解
print("最小范数解为:", x)运行结果:
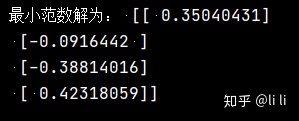
例:求下列矛盾方程组的最小二乘解.
from numpy import array
from numpy.linalg import pinv
A = array([[1, 1], [2, 2], [1, 2]])
b = array([1, 3, 2])
b.resize(3, 1)
x = pinv(A).dot(b) # 求最小二乘解
print("最小二乘解为:", x)运行结果:
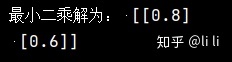
特征值与特征向量:
例:求下列矩阵的特征值和特征向量.
import numpy as np
from numpy.linalg import eig
A = np.array([[0, -2, 2], [-2, -3, 4], [2, 4, -3]])
values, vectors = eig(A)
print("A的特征值为:", values)
print("A的特征向量为:", vectors)运行结果:

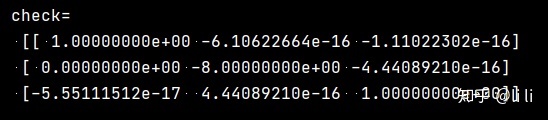
例:对于矩阵
from numpy import array, dot
from numpy.linalg import eig, inv
A = array([[0, -2, 2], [-2, -3, 4], [2, 4, -3]])
values, vectors = eig(A)
check = dot(inv(vectors), A).dot(vectors)
print("check=n", check)运行结果:
3)求超定线性方程组的最小二乘解 参考:pyhton scipy最小二乘法(scipy.linalg.lstsq模块) numpy的ones_like函数_christne1225i的专栏-CSDN博客 np.c_和np.r_的用法解析_demonszjin-CSDN博客
求超定线性方程组
import numpy as np
import numpy.linalg as LA
from matplotlib.pyplot import plot, rc, legend, show, savefig
x = np.array([0, 1, 2, 3])
y = np.array([-1, 0.2, 0.9, 2.1])
A = np.c_[x, np.ones_like(x)]
m, c = LA.lstsq(A, y, rcond=None)[0]
print(m, c)
rc('font', size=16)
plot(x, y, 'o', label='原始数据', markersize=5)
plot(x, m * x + c, 'r', label='拟合直线')
rc('font', family='SimHei') # 用来正常显示中文标签
rc('axes', unicode_minus=False) # 用来正常显示负号
legend()
savefig("figure3_41.png", dpi=500)
show()运行结果:
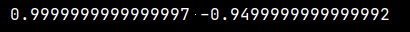
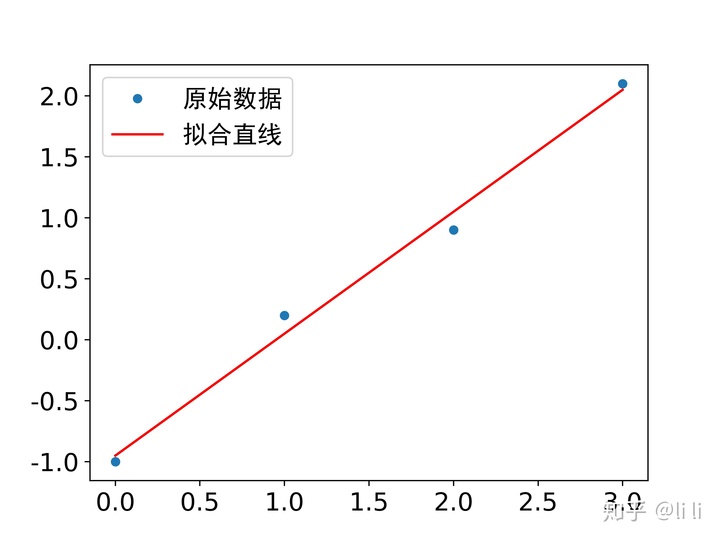
例:为了测量刀具的磨损速度,做这样的实验:经过一段时间(如每隔1小时),测量一次刀具的厚度,得到一组实验数据
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 27.0 | 26.8 | 26.5 | 26.3 | 26.1 | 25.7 | 25.3 | 24.8 |
import numpy as np
import numpy.linalg as LA
import matplotlib.pyplot as plt
t = np.arange(8)
y = np.array([27.0, 26.8, 26.5, 26.3, 26.1, 25.7, 25.3, 24.8])
A = np.c_[t, np.ones_like(t)]
ab = LA.lstsq(A, y, rcond=None)[0] # 返回值为向量
print(ab)
plt.rc('font', size=16)
plt.plot(t, y, 'o', label='Original data', markersize=5)
plt.plot(t, A.dot(ab), 'r', label='Fitted line')
plt.legend()
plt.savefig("figure3_42.png", dpi=500)
plt.show()运行结果:

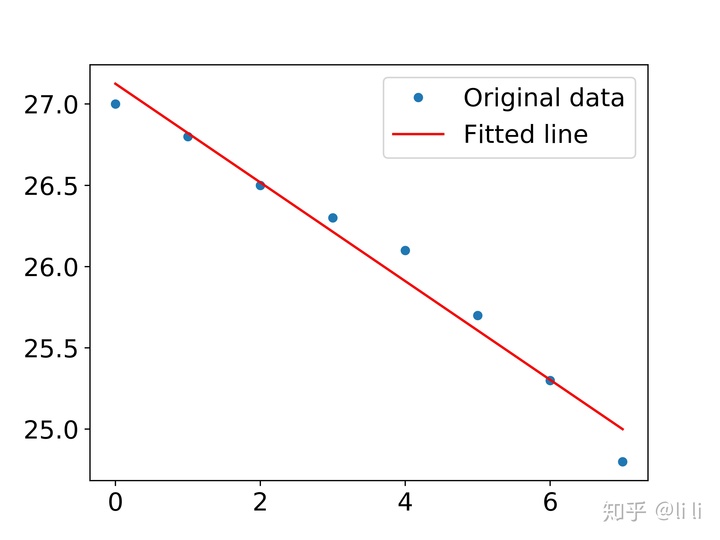
最后
以上就是玩命眼神最近收集整理的关于有理数python_Python数学实验与建模(3)的全部内容,更多相关有理数python_Python数学实验与建模(3)内容请搜索靠谱客的其他文章。








发表评论 取消回复