Python数学实验与建模课后习题第2章解析习题2

60 阅读 0 评论 40 点赞

我是靠谱客的博主忧虑季节，最近开发中收集的这篇文章主要介绍Python数学实验与建模课后习题第2章解析习题2，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

习题2

2.1 考虑下面的 $3 \times 4$ 矩阵

$\ 5 & 6 &7&8\ 9&10&11&12 end{bmatrix} quad$
（1）使用array函数在Python中构建该矩阵

A = np.array(((1, 2, 3, 4), (5, 6, 7, 8), (9, 10, 11, 12)))

（2）使用arange函数构造该矩阵

A = np.arange(1, 13).reshape(3, 4)

（3）表达式A[2,:]的结果是什么？类似的表达式A[2:]的结果是什么？

[ 9 10 11 12]
[[ 9 10 11 12]]

2.2 构造范德蒙德矩阵（Vandermonde matrix）

$\ 1 & 2 &4&8 \1&3&9&27 \1&4&16&64 end{bmatrix} quad$
提示：Numpy模块中可以通过vander命令直接构建

v = np.array([1,2,3,4])
V = np.vander(v, increasing=True)

numpy.vander使用方法
numpy.vander(x, N=None, increasing=False) 生成范德蒙矩阵。

2.3 令 $v=[1,-1,1]^T$ ，构造如下投影矩阵：

$P=frac{vv^T}{v^Tv} 和Q=I-P$

v = np.array([[1, -1, 1]]).T
P = np.dot(v,v.T)/np.dot(v.T,v)
I = np.eye(3)
Q = I - P

2.4 编写程序，生成包含1000个0~100内的随机整数，并统计每个元素的出现次数

import random
x = [random.randint(0, 100) for i in range(1000)]
d = set(x)
print(d)
for i in d:
    print(i, ':', x.count(i))

2.5 编写程序，生成包含20个随机数的数组，然后将前10个元素升序排列，后10个元素降序排列，并输出结果

import numpy as np
x = np.random.randint(100, size=20)
x[0:10].sort()  # 前10个元素升序排列
x[10:20] = abs(np.sort(-x[10:20]))  # 后十个元素降序排列

2.6 求矩阵 $&205&40\ 90 & -60 &96&1\210&-3&101&89end{bmatrix}quad$ 的鞍点，即该位置上的元素是该行上的最大值，是该列上的最小值。矩阵可能存在多个鞍点，也可能没有鞍点

import numpy as np

A = np.array([[9, 80, 205, 40],
              [90, -60, 96, 1],
              [210, -3, 101, 89]])

for i in range(A.shape[0]):
    for j in range(A.shape[1]):
        if A[i][j] == max(A[i]) and A[i][j] == max(A[:, j]):
            print('鞍点为：', A[i][j])

2.7 假设有一个英文文本文件，编写程序读取其内容，并将其中的大写字母变为小写字母，小写字母变为大写字母。

f = open('problem.txt', 'r', encoding='utf-8')  # 为输入打开一个文本文件
s = f.read()  # 读取
s = s.swapcase()  # 大小写互换
f = open('problem.txt', 'w', encoding='utf-8')  # 为输出建立一个新的文本文件
f.write(s)
f.close()

2.8 在同一个图形界面中分别画出6条曲线

$y=kx^2sin(x)+2k+cos(x^3),k=1,2,...,6$
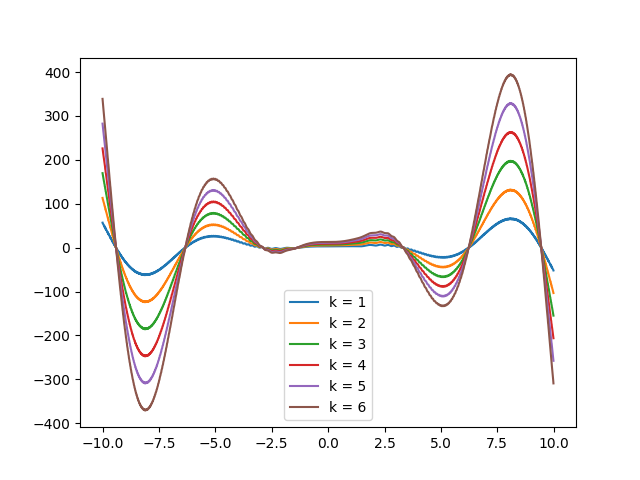
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-10, 10, 0.01)
plt.figure()
for i in range(6):
    k = i + 1
    y = k * x ** 2 * np.sin(x) + 2 * k + np.cos(x ** 3)
    text = 'k = ' + str(k)
    plt.plot(x, y, label=text)

plt.legend()
plt.show()

2.9 把屏幕开成2行3列6个子窗口，每个子窗口画一条曲线，画出曲线

$y=kx^2sin(x)+2k+cos(x^3),k=1,2,...,6$
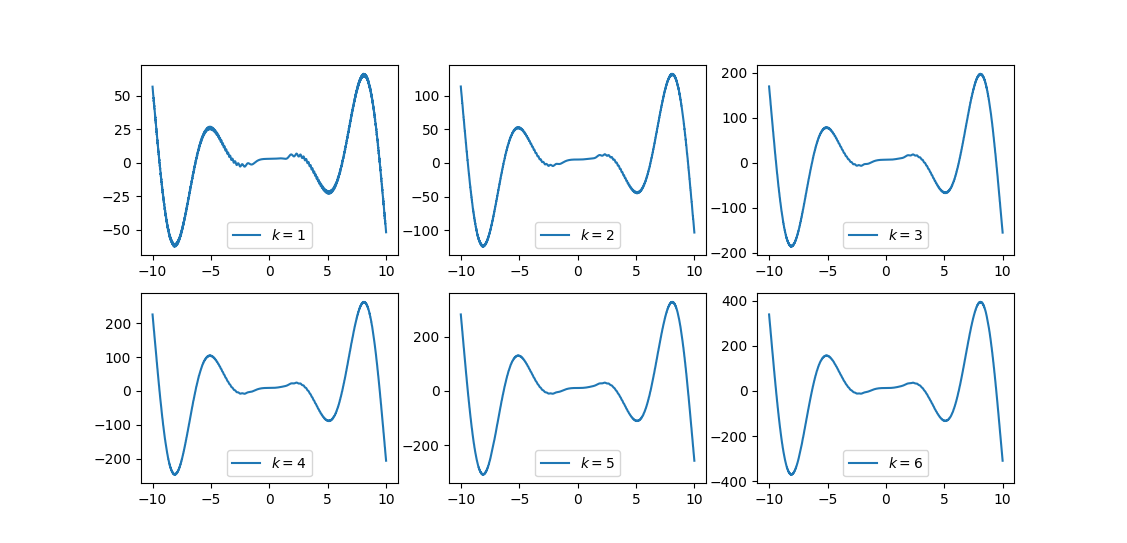
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-10, 10, 0.01)
plt.figure()
for i in range(6):
    k = i + 1
    ax = plt.subplot(2, 3, k)
    y = k * x ** 2 * np.sin(x) + 2 * k + np.cos(x ** 3)
    text = '$k = ' + str(k) + '$'
    plt.plot(x, y, label=text)
    plt.legend()
plt.show()

2.10 分别画出下列二次曲面：

（1）单叶双曲面
$frac{x^2}{8}+frac{y^2}{10}-frac{z^2}{6}=1$
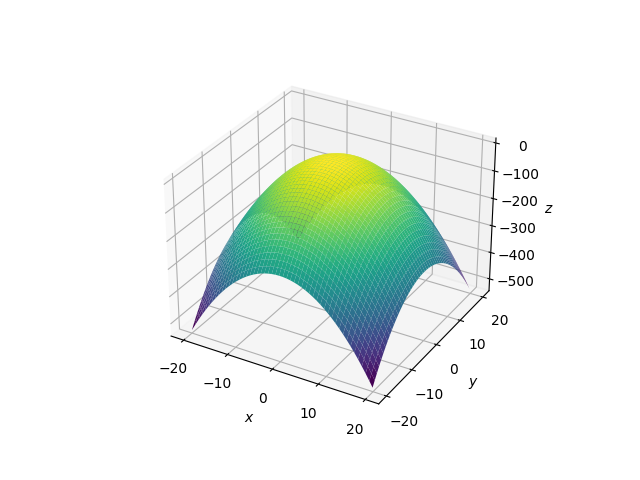
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-20, 20, 0.1)
y = np.arange(-20, 20, 0.1)
X, Y = np.meshgrid(x, y)
ax = plt.subplot(1, 1, 1, projection='3d')
Z = (1 - X ** 2 / 8 - Y ** 2 / 10) * 6
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$y$')
ax.set_zlabel(r'$z$')
plt.show()

（2）双叶双曲面
$frac{x^2}{8}-frac{y^2}{12}-frac{z^2}{8}=1$
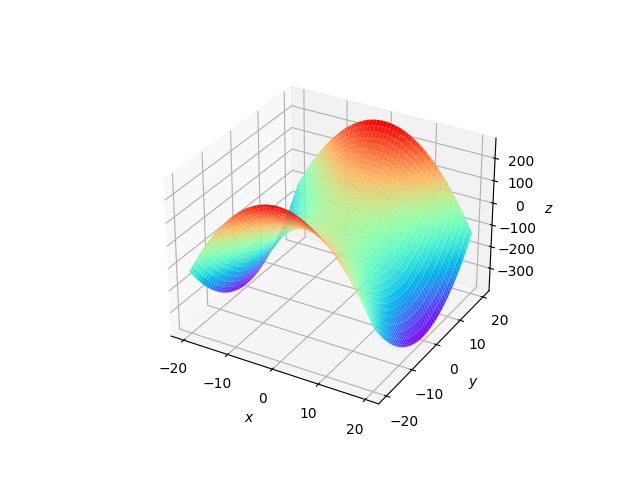
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-20, 20, 0.1)
y = np.arange(-20, 20, 0.1)
X, Y = np.meshgrid(x, y)
ax = plt.subplot(1, 1, 1, projection='3d')
Z = (1 - X ** 2 / 8 + Y ** 2 / 12) * 8
ax.plot_surface(X, Y, Z, cmap='rainbow')
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$y$')
ax.set_zlabel(r'$z$')
plt.show()

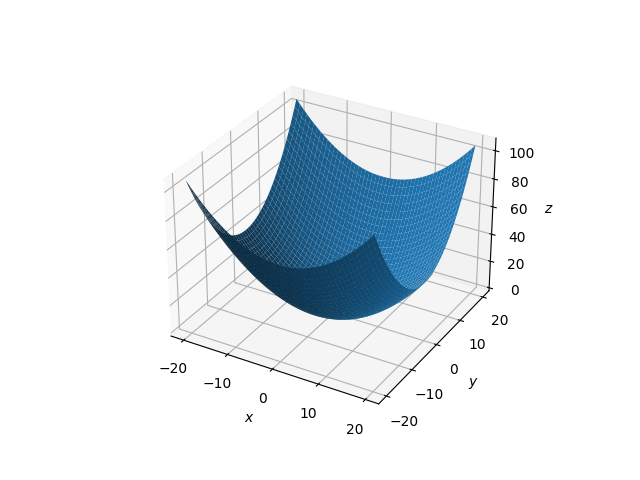
（3）椭圆抛物面
$frac{x^2}{10}+frac{y^2}{6}=z$
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-20, 20, 0.1)
y = np.arange(-20, 20, 0.1)
X, Y = np.meshgrid(x, y)
Z = X ** 2 / 10 + Y ** 2 / 6
ax = plt.subplot(1, 1, 1, projection='3d')
ax.plot_surface(X, Y, Z)
ax.set_xlabel(r'$x$')
ax.set_ylabel(r'$y$')
ax.set_zlabel(r'$z$')
plt.show()

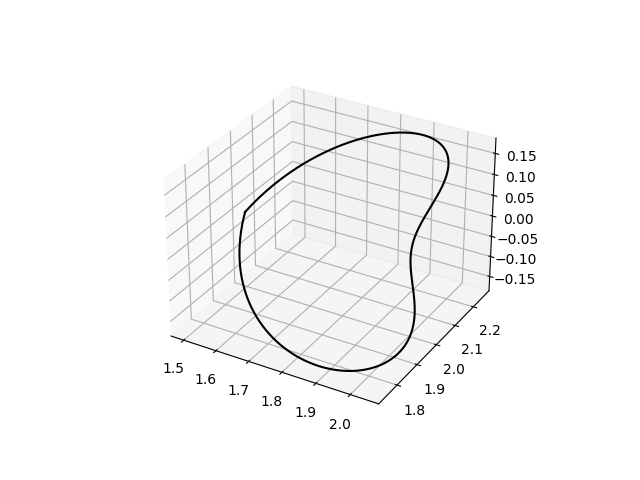
2.11 莫比乌斯带是一种拓扑学结构，它只有一个面和一个边界，是1858年德国数学家、天文学家莫比乌斯和约翰·李斯丁独立发现的，其参数方程为 $\y=left(2+frac{s}{2} cos frac{t}{2}right) sin t \z=frac{s}{2} sin frac{t}{2}end{array}right.$ 其中， $0 \leq t \leq 2 π, - 1 \leq s \leq 1$ 。绘制莫比乌斯纽带

在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

ax = plt.axes(projection='3d')
s = np.linspace(-1, 1, 1000)
t = np.linspace(0, 2 * np.pi, 1000)
x = (2 + s / 2 * np.cos(t / 2) * np.cos(t))
y = (2 + s / 2 * np.cos(t / 2) * np.sin(t))
z = s / 2 * np.sin(t / 2)
ax.plot3D(x, y, z, 'k')
plt.show()

2.12 画出如下函数的等高线，并进行标注

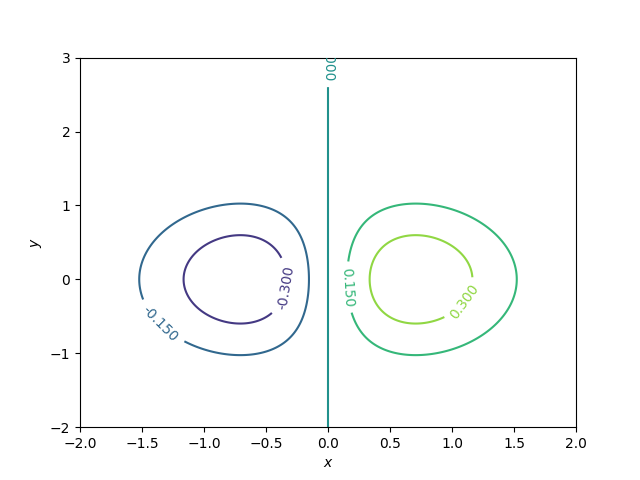
（1） $z=xe^{-x^2-y^2},-2leq xleq 2,-2leq yleq3;$
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-2, 2, 1000)
y = np.linspace(-2, 3, 2000)
z = np.zeros((len(y), len(x)))
for i in range(len(x)):
    for j in range(len(y)):
        z[j][i] = x[i] * np.exp(-x[i] ** 2 - y[j] ** 2)
contr = plt.contour(x, y, z)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.clabel(contr)
plt.show()

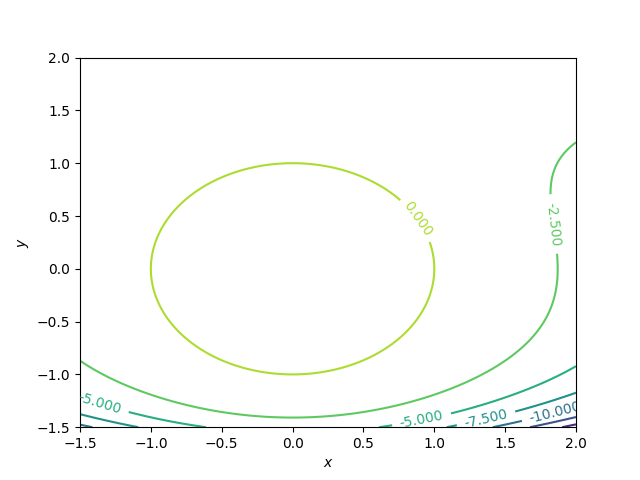
（2） $z=(1-x^2-y^2)e^{frac{-y^3}{3}},-1.5leq x leq2,-1.5leq yleq2$
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1.5, 2, 1000)
y = np.linspace(-1.5, 2, 2000)
z = np.zeros((len(y), len(x)))
for i in range(len(x)):
    for j in range(len(y)):
        z[j][i] = (1-x[i]**2-y[j]**2)*np.exp(-y[j]**3/3)
contr = plt.contour(x, y, z)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.clabel(contr)
plt.show()

2.13 附件1：区域高程数据.xlsx（数据见封底二维码）给出了某区域 $43.65 k m \times 58.2 k m$ 的高程数据，画出该区域的三维网格图和等高线图，在A(30,0)和B(43,30)（单位：km）点处建立了两个基地，在等高线图上标注出这两个点。

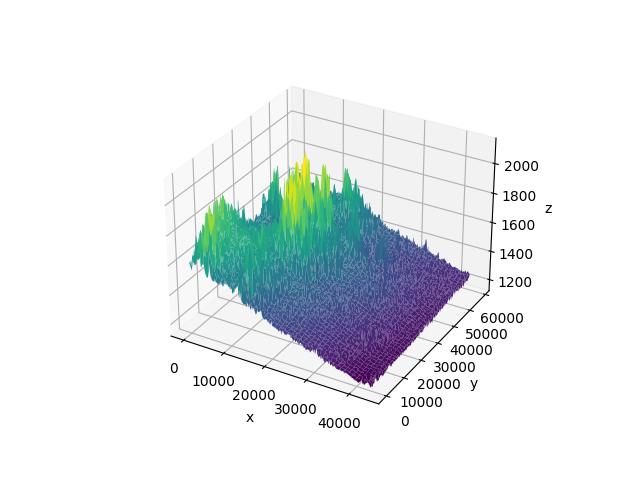
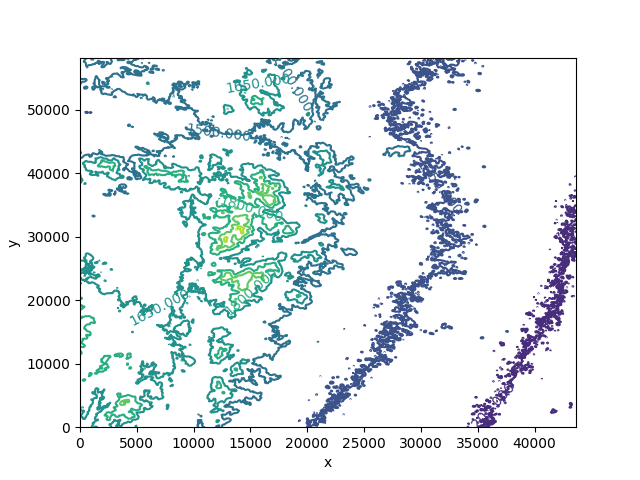
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

z = np.zeros((1165, 874))
x = np.arange(0, 50 * 874, 50)
y = np.arange(0, 50 * 1165, 50)
excel = pd.read_excel('附件1：区域高程数据.xlsx', header=None)  # 不加索引
excel = excel.drop([874, 875, 876, 877])  # 去掉无用行数据

for i in range(874):  # 把excel二维数组存储到Python中
    for j in range(1165):
        z[j][i] = int(excel.iloc[i, j])

ax = plt.axes(projection='3d')
X, Y = np.meshgrid(x, y)
ax.plot_surface(X, Y, z, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

contr = plt.contour(x, y, z)
plt.xlabel('x')
plt.ylabel('y')
plt.clabel(contr)
plt.show()