机器学习基石 Lecture11: Linear Models for Classification

Linear Models for Binary Classification

目前学了三种线性模型，其中都包含了$w^{T}x$的部分，他们之间的区别如下，能否使用线性回归或是逻辑回归的方法来帮助实现线性分类呢？

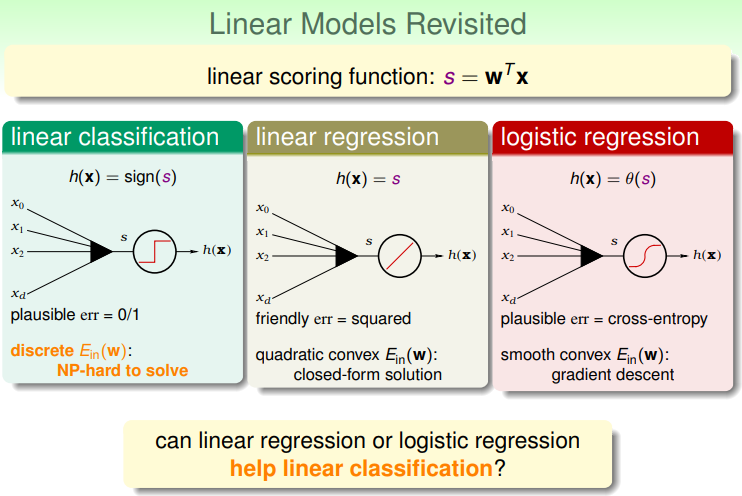
它们之间的区别主要是体现在error函数上面，对于一个二元分类的问题来说，这三种算法的error函数可以写为如下形式：

将这几种模型的error函数进行可视化，可以发现它们之间存在一定的大小关系：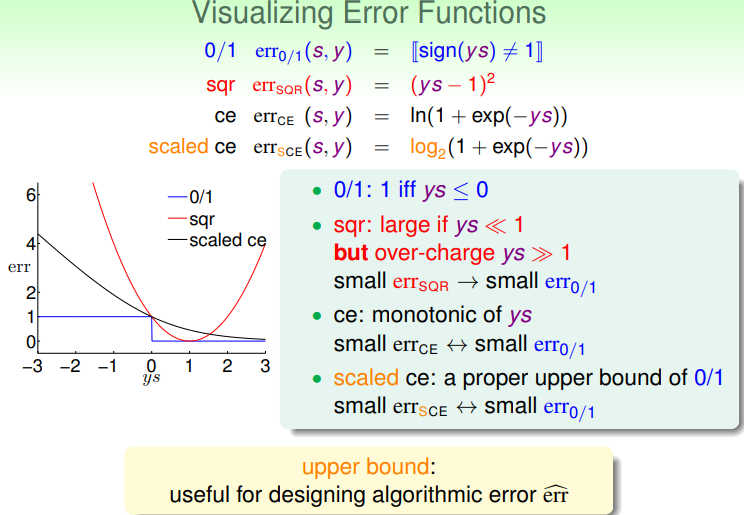
也就是，线性回归的平方误差，与逻辑回归的scaled交叉熵误差，都可以作为0/1误差的一个上界，而上界正是使用算法时需要的东西。因此如果将线性回归的平方误差与逻辑回归的scaled交叉熵误差作为线性分类问题的0/1误差的上界的话，依然能够保证线性分类问题的$E_{in}^{0/1}(w)$误差上界与$E_{out}^{0/1}(w)$有较小的保证。这也就意味着能够使用线性回归和逻辑回归来做线性分类的问题：
当然这三种方法都各自有各自的优缺点，后两种方法得到的上限都比较宽松：
线性回归方法有时候会先用来得到一个结果作为PLA或pocket PLA或者逻辑回归方法的初始值$w_0$。而且逻辑回归一般会相对于pocket PLA更优先使用。

Stochastic Gradient Descent

回顾一下两种迭代式求解的方法。PLA每次迭代只需要对一个样本进行计算，因此复杂度是$O(1)$。而逻辑回归或者pocketPLA算法每一次对系数的更新都要遍历所有的样本，也就是复杂度为$O(N)$。如果能够使得逻辑回归每次更新也是$O(1)$复杂度就好了。确实有这样的方法，那就是使用一个样本点上的随机梯度来替代真实的梯度：
而这种方法就叫做随机梯度下降法（stochastic gradient descent）。这个方法的思路就是使用随机的梯度来替代真实的梯度值。这样做在足够多步骤之后，得到的结果期望是与使用真实梯度一样的。因此这样做的好处是能够极大减少计算量，对于大量数据和在线数据很有好处。不过坏处就是更不稳定。
而去掉了平均之后的更新方式看起来很熟悉，和PLA里的更新公式很类似。只不过把判断是否与y不相等改为了不相等的概率。因此当步长$\eta =1$而乘积特别大的时候，两种算法很接近：
而对于随机梯度下降法有两点需要注意，一个是不太好把握最终结束的条件，一般是使用迭代次数$t$足够大。而$\eta$的选择也很重要，经验值为0.1附近效果比较好。

Multiclass via Logistic Regression

如何将逻辑回归应用到多分类的问题上呢？假设现在有4类的点需要分类：

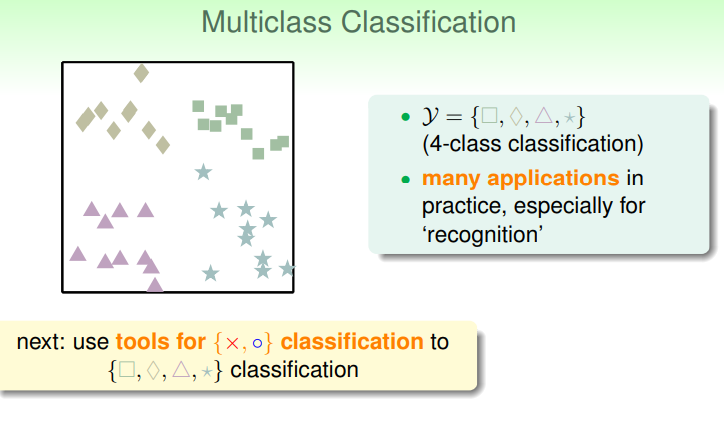
如果每一次只针对一个类别进行分类，那么可以使用多个线性分类器，组合起来得到最终的多分类结果，这时对于N个类别就需要有N个分类器：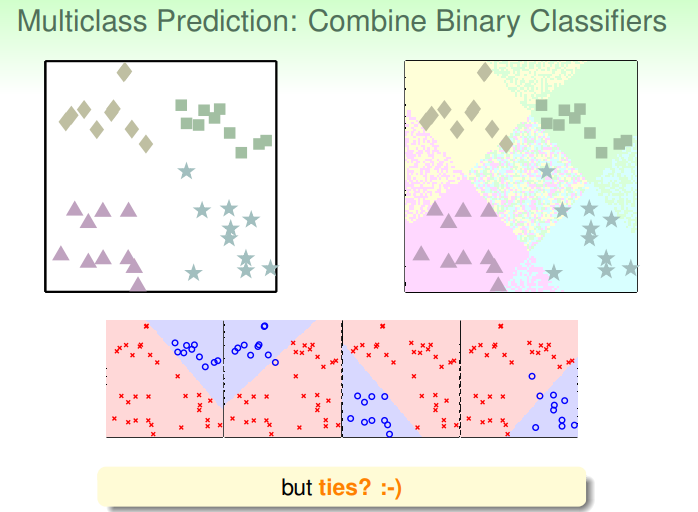
但是使用这样的分类器，可能会遇到一种情况就是对应不同类别的分类器都判断某个点属于它对应的类（+1），或者有可能有每个分类器都认为其不属于自身对应的类（-1）的情况。这样的事情就很难解决。而如果把对应的每个分类器改为逻辑回归的函数，每个分类器得到的是属于本类的概率，这样的话最终取不同分类器里概率最大的那个即可：

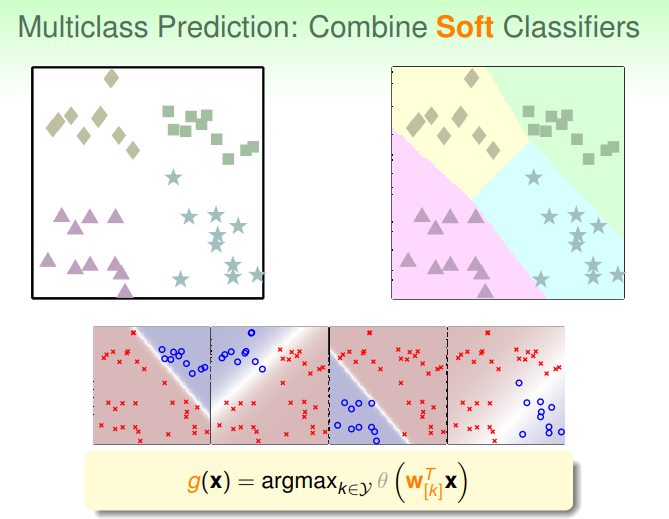
这样每次对多类别的数据只进行一个类别的判断的方法叫做One-vs-All（OVA）分解。算法如图：

这样做的好处是比较高效，并且可以利用类似逻辑回归的算法。但坏处是它对于类别K比较多，而数据比较不均衡的时候处理的不好。比如有100个点有100类，每次分类器得到的结果可能都是返回不属于本类（概率为0），因为这样做的error就已经非常小了。
不过OVA算法依然是一个适于使用的一类算法。

Multiclass via Binary Classification

为了解决上述OVA方式对于unbalanced数据表现较差的问题又有一个想法，那就是我们每次选择两个类别的数据进行分类而不管其它的数据。这样想是因为OVA里正负比例不平衡的原因在于负例里对应的类别太多也就导致样本太多。改为每次分类两种可以解决这个问题：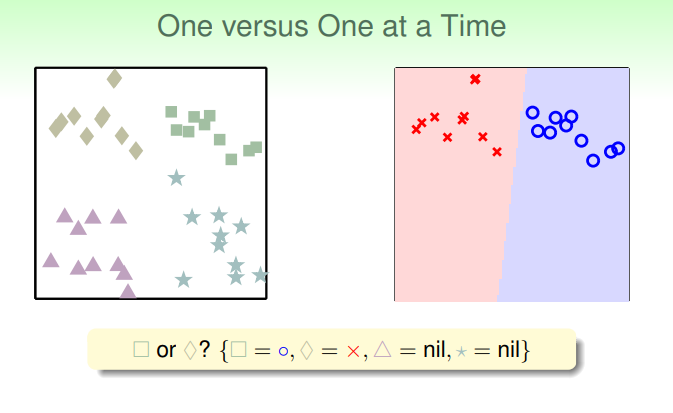
因此这样最终就会有$C_n^2$个二分类器，应用所有的分类器，选择被分为正类次数最多的类型作为最终结果：

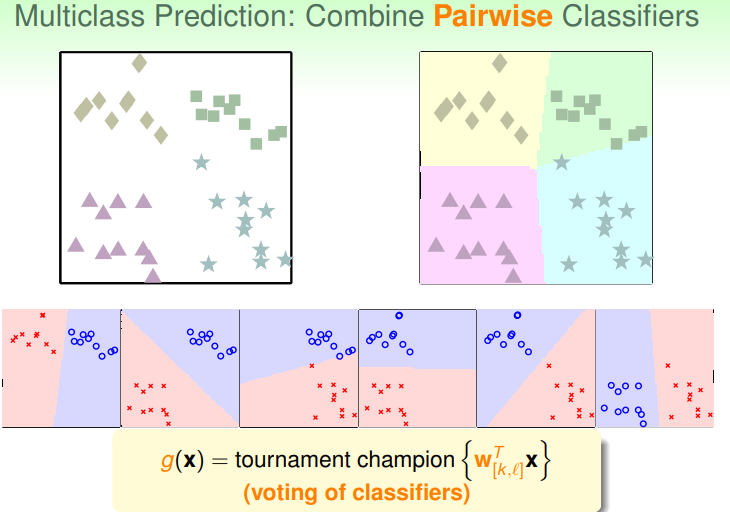
算法流程如图：

这个方法也有自己的优缺点。**优点：**更高效（每次针对的分类问题较小），更稳定，可以使用任意的二元分类方法。 **缺点：**使用了$O(K^2)$级别数量的分类器。这会导致需要更多空间，更多时间，更多训练。不过这个算法同样也是一个可以应用的实际算法。

最后

以上就是个性超短裙为你收集整理的机器学习基石 Lecture11: Linear Models for Classification的全部内容，希望文章能够帮你解决机器学习基石 Lecture11: Linear Models for Classification所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。