问题背景

神经网络建模


本实例采用一种简单的个人客户信贷信用评估方法,对所有客户做二分类,只区分好和差两种情况。数据采用德国信用数据库。德国信用数据库由Hans Hofmann教授整理,包含1000份客户资料,每位客户包含20条属性,并给出了信用的好或差的标注。数据库可从以下网址下载得到:
![]()
除了原始数据,该数据库还给出了数据的说明。原始数据保存在german.data文件中,包含7个数值属性,13个类别属性,以及一个分类标签,以下给出粗略的介绍:


部分样本如下表所示:
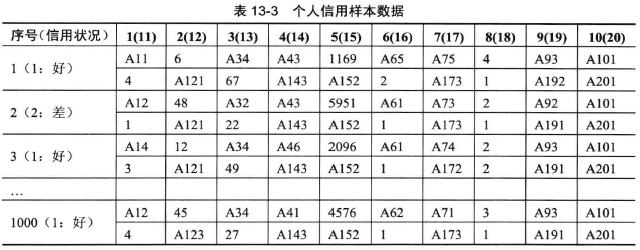
其中的数值属性可以直接使用,类别属性经过整数编码后可以使用。观察上文给出的20中个人用户属性,可以发现不少信息发生了部分重叠,然而,在神经网络中,用户可以忽略这些细节,由网络来完成映射关系。
此外,该数据库还给出了另一个处理过的文件german.data-numeric,将原始文件的类别属性进行了整数编码,形成了24个数值属性,可以直接使用。本实例将主要使用原始数据进行评估,最后也会给出结果。
使用MATLAB实现一个三层的BP神经网络。由于每个个人用户拥有24个属性,因此输入层包含24个神经元节点。该问题为针对信用好/差的二分类问题,因此输出层只包含一个神经元。隐含层的神经元个数与网络性能有关,需要通过实验确定,建立的神经网络结果如图:
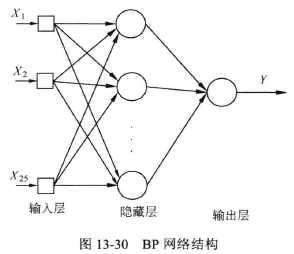
个人信贷信用评估的实现
使用文件german.data提供的1000×20属性及分类标签作为数据构建BP神经网络,完成个人信贷的信用评估。具体流程如下图所示:
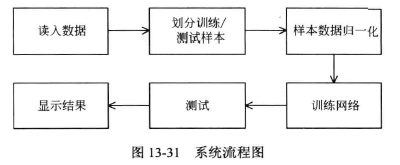
(1)读入数据。由于数据保存在二进制文件german.data中,需要使用MATLAB的读入函数textcsan。调用方法如下:
C = textscan(fileID,formatSpec)
其中FID为打开的文件句柄,字符串formatSpec表示读取时的格式。读取数据的代码如下:
%% 读入数据
% 打开文件
fid = fopen('german.data', 'r');
% 按格式读取每一行
% 每行包括21项,包括字符串和数字
C = textscan(fid, '%s %d %s %s %d %s %s %d %s %s %d %s %d %s %s %d %s %d %s %s %dn');
% 关闭文件
fclose(fid);执行上述代码,二进制文件中是数据就被读到变量C中。C是一个1×21的细胞数组,对应20个属性和信用状况。细胞数组的每一个元素均包含了1000个样本数据,如果该属性为数值属性,则该元素为1000×1列向量,否则元素本身又是一个包含1000个字符串的细胞数组:
C =
1 至 9 列
{1000x1 cell} [1000x1 int32] {1000x1 cell} {1000x1 cell} [1000x1 int32] {1000x1 cell} {1000x1 cell} [1000x1 int32] {1000x1 cell}
10 至 18 列
{1000x1 cell} [1000x1 int32] {1000x1 cell} [1000x1 int32] {1000x1 cell} {1000x1 cell} [1000x1 int32] {1000x1 cell} [1000x1 int32]
19 至 21 列
{1000x1 cell} {1000x1 cell} [1000x1 int32]为了便于计算,必须使用数值来表示数据中的类别属性。最简单的方式就是使用整数进行编码,如第一个属性的类别字符串为“A12”,“A1”表示该属性为第一个属性,“2”表示属性值为第二个类别。因此,采用数字“2”编码字符串“A12”,具体实现如下:
% 将字符串转换为整数
N = 20;
% 存放整数编码后的数值矩阵
C1=zeros(N+1,1000);
for i=1:N+1
% 类别属性
if iscell(C{i}) % Determine whether input is cell array
for j=1:1000
% eg: 'A12' -> 2
if i<10
d = textscan(C{i}{j}, '%c%c%d');
% eg: 'A103' -> 3
else
d = textscan(C{i}{j}, '%c%c%c%d');
end
C1(i,j) = d{end};
end
% 数值属性
else
C1(i,:) = C{i};
end
end得到的矩阵C1位21×1000数组矩阵。
(2)划分训练样本与测试样本。在全部1000份样本中,共有700份正例(信誉好)300份负例(信誉差)。划分时取前350份正例和前150负例作为训练样本,后350正例和后150份负例作为测试样本:
%% 划分训练样本与测试样本
% 输入向量
x = C1(1:N, :);
% 目标输出
y = C1(N+1, :);
% 正例
posx = x(:,y==1);
% 负例
negx = x(:,y==2);
% 训练样本
trainx = [ posx(:,1:350), negx(:,1:150)];
trainy = [ones(1,350), ones(1,150)*2];
% 测试样本
testx = [ posx(:,351:700), negx(:,151:300)];
testy = trainy;(3)样本归一化。使用mapminmax函数对输入样本进行归一化,由于输出样本只取1和2两个值,因此目标输出不做归一化。
%% 样本归一化
% 训练样本归一化
[trainx, s1] = mapminmax(trainx);
% 测试样本归一化
testx = mapminmax('apply', testx, s1);(4)创建BP神经网络,并完成训练:
%% 创建网络,训练
% 创建BP网络
net = newff(trainx, trainy);
% 设置最大训练次数
net.trainParam.epochs = 1500;
% 目标误差
net.trainParam.goal = 1e-13;
% 显示级别
net.trainParam.show = 1;
% 训练
net = train(net,trainx, trainy);在这里,采用newff函数创建一个BP神经网络,隐含层节点个数及传递函数均采用默认值,训练函数采用默认的trainlm函数,设定最大迭代次数为1500次,然后调用train函数进行训练。
(5)测试。BP网络输出值并不限定为1或2,而是一个实数,因此还需要将输出转换为整数。取1.5为阈值,小于该阈值的输出判为1(信用好),否则判为2(信用差)。
%% 测试
y0 = net(testx);
% y0为浮点数输出。将y0量化为1或2。
y00 = y0;
% 以1.5为临界点,小于1.5为1,大于1.5为2
y00(y00<1.5)=1;
y00(y00>1.5)=2;
% 显示正确率
fprintf('正确率: n');
disp(sum(y00==testy)/length(y00));BP神经网络取得了较为理想的正确率,测试的输出结果为:
正确率:
0.7500
(6)显示结果。为了抵消随机因素的影响。取相同的训练和测试样本运算20次,统计正确率与迭代次数。将第(4)和第(5)步的代码改为:
%% 训练.测试
M = 20;
rat = zeros(1, M);
trr = rat;
for i=1 : M
% 创建网络,训练
net = newff(trainx, trainy);
% 设置最大训练次数
net.trainParam.epochs = 1500;
% 目标误差
net.trainParam.goal = 1e-13;
% 显示级别
net.trainParam.show=1;
% 训练
[net tr] = train(net, trainx, trainy);
% 测试
y0 = net(testx);
% y0为浮点数,将y0量化为1或2
y00 = y0;
y00(y00<1.5) =1;
y00(y00>1.5) =2;
rat(i) = sum(y00==testy)/length(y00);
trr(i) = length(tr.epoch);
end
% 显示正确率
fprintf('正确率:n');
disp(rat);
fprintf('平均正确率:n');
disp(mean(rat));
fprintf('最低正确率:n');
disp(min(rat));
% 显示训练次数
fprintf('迭代次数:n');
disp(trr);
% 绘制双坐标图
[AX, H1, H2] = plotyy(1:M, rat, 1:M, trr, 'plot', 'plot');
% 设置y轴的范围
set(AX(1), 'YLim', [0.70, 0.80]);
set(AX(2), 'YLim', [0, 5]);
% 设置线型
set(H1, 'LineStyle', '--')
set(H2, 'LineStyle', ':')
% 设置Y轴标签
set(get(AX(1), 'Ylabel'), 'String', '正确率')
set(get(AX(2), 'Ylabel'), 'String', '训练次数')
title('BP网络的正确率与训练次数')运算20次,可得到每一次测试的正确率及迭代次数:
正确率:
1 至 8 列
0.7560 0.7460 0.7620 0.7640 0.7580 0.7480 0.7560 0.7460
9 至 16 列
0.7600 0.7500 0.7520 0.7500 0.7480 0.7620 0.7500 0.7600
17 至 20 列
0.7680 0.7620 0.7440 0.7380
平均正确率:
0.7540
最低正确率:
0.7380
迭代次数:
1 至 13 列
4 4 4 4 4 4 4 4 4 4 4 4 4
14 至 20 列
4 4 4 4 4 4 4测试20次的平均正确率为75.4%,最低正确率为73.8%,迭代次数均为4。绘制的双坐标图如下:
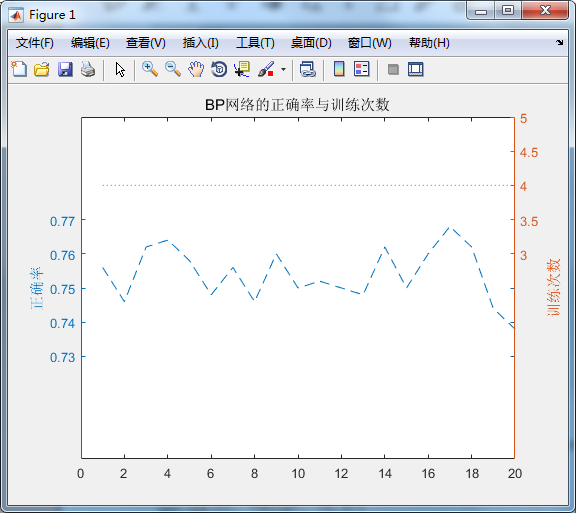
如上图所示,正确率曲线大致稳定在0.74~0.76之间,迭代次数则稳定在4次。使用BP神经网络对实际信用数据实现了较好的预测。在采用350份正例和150份负例作为训练样本的情况下,以75%的正确率成功预测了新客户的信贷信用情况。
最后
以上就是精明舞蹈最近收集整理的关于MATLAB实现基于BP网络的个人信贷信用评估问题背景神经网络建模个人信贷信用评估的实现的全部内容,更多相关MATLAB实现基于BP网络内容请搜索靠谱客的其他文章。








发表评论 取消回复