下面的文章讲的很好,但有一些繁琐。
首先注意的是坐标系是左上角为坐标原点,向右递增为x轴,向下递增为y轴。
画图关键就是用简单的三角函数sin cos根据区间所占比例来画图。
另外推荐两个验证网页的工具:
http://validator.w3.org/check 用于测试网页是否valid
http://gsnedders.html5.org/outliner/process.py 用来解析网页的outline
In previous articles, Jake introduced you to Scalable Vector Graphics, or SVG. Unlike other graphics formats, an SVG file is simply XML (text with angle brackets, for those who haven't been paying attention), which makes it particularly well suited to being generated on-the-fly by an agent. There are other ways to create graphics on demand, but none are anywhere near as simple, cheap and elegant as SVG.
There are currently a couple of drawbacks to SVG. These are not inherent to the SVG format, but are due to the current browser plugins required to view the file. They simply aren't as mature as, say, the Flash viewer, and are a wee bit on the slow side. That means that we need to keep the graphics fairly simple in order to produce reasonable render times. Since the main purpose of SVG elements in a Domino web application will be to produce graphs and charts, that shouldn't be a problem -- just try to avoid complexGISmaps in production until the viewers catch up.
In addition, we need to keep the Domino elements used to generate the code relatively simple and quick. People have gotten used to waiting for a page to download once in a while, but they tend not to wait forever for graphics. If your agent is too complex, the delay between the page being rendered and the graphic appearing will be too long for most users. (This will be less of a problem when we can safely use multiple XML namespaces in a single web document, since we will be able to serve the graphic and its host page at the same time. Realistically, that means waiting until Microsoft Internet Explorer supports multiple namespaces inline.) Depending on the data you want to present, this may mean using two separate agents: a scheduled agent to collect the data and save it in a document, and a second to serve the data to the web. (The web agent is needed pre-Domino 6 to ensure that the output has the correct content-type. Netscape/Mozilla is especially fussy about content-type.) Since pie charts will require some complex calculation, we will generally use two agents to create and serve the chart.
What we want to draw
First, we should take a look at the sort of result we want to achieve. This is a simple pie chart in SVG format:
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="400" height="400"> <!-- Pie chart sample --> <path d="M200,200 L200,20 A180,180 0 0,1 377,231 z" style="fill:#ff0000; fill-opacity: 1; stroke:black; stroke-width: 1"/> <path d="M200,200 L377,231 A180,180 0 0,1 138,369 z" style="fill:#00ff00; fill-opacity: 1; stroke:black; stroke-width: 1"/> <path d="M200,200 L138,369 A180,180 0 0,1 20,194 z" style="fill:#0000ff; fill-opacity: 1; stroke:black; stroke-width: 1"/> <path d="M200,200 L20,194 A180,180 0 0,1 75,71 z" style="fill:#ff00ff; fill-opacity: 1; stroke:black; stroke-width: 1"/> <path d="M200,200 L75,71 A180,180 0 0,1 200,20 z" style="fill:#ffff00; fill-opacity: 1; stroke:black; stroke-width: 1"/> </svg>
Copy the text and paste it into a text editor (Notepad will do just fine if you haven't gotTextpadyet), then save it as a file with the extension ".svg". Open the file in an SVG viewer (download the Adobe SVG viewer if you don't have it yet) to take a look at the chart. What you should see is a top-on flat pie chart without labels or any other embellishments. In other words, this is as simple as it's going to get. If all has gone well, the chart should look something like this:
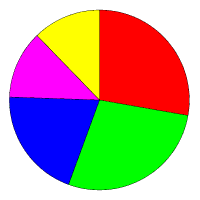
There are five segments to this chart, each of which is defined by one of the <path> elements in the SVG source text. Nothing to it, eh? So let's take a look at the <path> statement.
A Closer Look
<path d="M200,200 L200,20 A180,180 0 0,1 377,231 z" style="fill:#ff0000; fill-opacity: 1; stroke:black; stroke-width: 1"/>
The <path> is the most versatile of the SVG primitives, since it can contain or create any of the other basic SVG shapes and describe things that none of the other basic types can, sort of the way a variant variable relates to other data types in LotusScript. Like a variant, it is more "expensive" than other types, so it's best left to those occasions when simpler (read: faster-rendering) primitives can't describe the shape. Since there is no <slice-of-pie> element, we need to use a <path>.
The shape of the path is defined by the "d=" part. There are a whole host of options for the "d=", but we are only interested here in the "M", "L", "A" and "Z" options. Yes, I know it's kind of cryptic, but once you learn to think in terms of the names rather than the abbreviations, it's actually pretty easy to get a grip on.
"M" ismoveTo, which allows us to move our imaginary pen anywhere on the "paper" without leaving a mark. In each of the pie slices, we start by moving to the centre of the circle. In the example, it is at the cooridinate (200,200) on a 400 by 400 "piece of paper".
Next is "L", orlineTo, which we will use to draw a line straight out from the centre to the appropriate spot on the circumference of the circle. The numbers following the "L" are the coordinates of the spot on the circumference that we want to go to.
Then we have "A" which is an ellipticalarcTo. Because the arcTo is elliptical, it takes quite a few arguments, so we'll have to break them down into bite-sized chunks:
A180,180 0 0,1 377,231
The first pair of numbers after the A, "180,180", are the radii that the arc will use. Since a circle is essentially an ellipse with identical radii in the "x" and "y" dimensions, both of the numbers are the same here. When we get around to fancier things, we'll take advantage of the two radii.
The second "group" is a zero all by its lonesome. This represents a rotation of the path around the centre relative to the x-axis of the "host" co-ordinate system. Translated, that means you can create slanted ellipses — a loverly thing, but not overly useful for pie charts. Leave the value at zero.
The next group, "0,1", is a pair of "flags". The first number is the "long arc flag". Since the arc is drawn between two points and the centre is not defined, we need a way to tell how far the arc has to go, otherwise an arc that covers more than half of the ellipse/circle will "shortcut" across the shape. When the arc is less than half of the whole circle, use a zero to tell the arc to use the shortest path. When it's longer than half, use a one to tell it to go the long way round. The second flag is a directional control. Zero is counter-clockwise in the Americas, but anticlockwise elsewhere. (If you remember back to Cartesian geometry lessons in school, proper mathematical angles are measured anticlockwise.) Clockwise arcs are drawn using a one as the flag value, and since that is the way that the Latin-alphabet-using eye usually moves around a circle, we'll present our data that way.
The final pair of numbers, "377,231", is the coordinate point at which the arc ends. How we arrive at that number will be covered later.
Finally, we arrive at the zed. "Z" is the closePath command. It's not mnemonically helpful to call closePath "Z", but it is the last thing you'll do in a path and will at least be familiar to anyone who has used the ancient CTRL-Z end-of-file marker. Once the path is closed, it can be filled with a colour or pattern without any unexpected effects on the rest of the "page".
The style elements should be pretty much self-explanatory to anyone who has used CSS with HTML, or to anyone who has used a vector drawing program. Essentially, we are setting the colour that will fill the slice of pie (the "fill") and the colour and width of the outline (or "stroke").
Now it's simply a matter of creating the right number of these slices, making them the right size, and putting them in the right place.
The Maths
Anyone who has been out of school for more than a couple of weeks (and who doesn't work with trigonometry on a regular basis) may need a bit of a refresher course in basic trigonometry, radians, and Cartesian coordinates. We'll need all of these to create our pie charts.
Let's start with the co-ordinate system. Most of us have gotten rather used to working with pixels and starting at the upper-left-hand corner of whatever "space" we are working in. While SVG coordinates tend to work the same way, we'll have to go back to the old-school way of thinking when we build the pie. In the standard Cartesian system, we have a horizontal x-axis (with positive numbers to the right of centre and negative numbers to the left of centre) and a vertical y-axis (with positive numbers above centre and negative numbers below centre), which cross each other at a point marked (0,0).
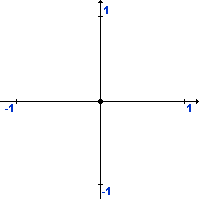
Okay, so that wasn't exactly higher maths -- but it gives us the space we need to work in to make the chart. Remember that we have to use an arc between two points to define the pie slice, so we have to figure out just what those two points will be. Since circles work on centres, radii and angles, while the SVG drawing space works on rectangular coordinates (how far across and how far down), we have to use trigonometry to convert between the two. Let's look at the whole circle in our co-ordinate space:
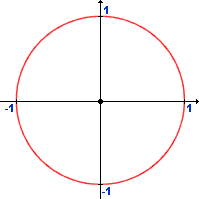
If that represents the total of our data set, and we want to show a "slice" of pie representing, say, one-third of the total, it's simply a matter of filling in one-third of the circle. One-third of 360 degrees is 120 degrees, so we just do this:
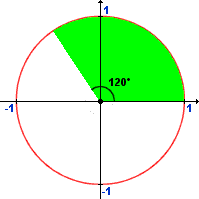
(In case you'd forgotten, angles are measured starting on the positive x-axis and going anticlockwise.) And that's exactly what we'd like to do — except that we can't. First, in using an angle, we've used the circle's natural (polar) coordinates, where we have to use rectangular coordinates. Second, we've gone and used degrees to measure the angle — and darned few computer languages do that. Formula Language, Java and LotusScript all useradians, which is a measure of an angle's "subtended arc length proportional to the radius of the arc".
For those of you who came to Domino from somewhere other than the world of maths, engineering or physics, all this means is that we'll have to stop thinking about circles having 360 degrees, and start thinking about them having 2πradians instead. (Think about it — the radius of a circle will fit around the circumference 2πtimes, so an angle that includes the whole circle will "subtend" or "hold within itself" an arc that is 2πtimes the radius in length.) Same concept, different numbers.
Now we have to concern ourselves with converting from "how much of the circle" to "how far over" and "how far down". There are a lot of really neat uses for trigonometry, but all we need to concern ourselves with for this task are these two universal truths: thesineof an angle will answer the question "how far up from zero", and thecosinewill answer "how far to the right of zero". By a happy coincidence, when the point needs to be to the left of or below the zero line, the corresponding sine or cosine value will be negative.
To create the first slice of pie, we need to know how much of the pie the slice will represent. That means having both the value that the slice represents and the total value for all slices. In keeping with the example above, let's say that the first slice represents one-third of the total. To find our angle, we multiply1/3by 2πradians. Taking the sine of the angle (using @Sin in Formula Language or the Sin function in LotusScript), we get approximately 0.866. The cosine (@Cos or Cos function) gives us -0.5. Our arcTo point, then, will lie 0.866 up from and 0.5 to the left of zero — which is exactly the same as we arrived at above. (When you create the actual agent, don't worry about rounding. Unlike a raster format like GIF or JPEG, SVG can deal with very exact mathematical coordinates.)
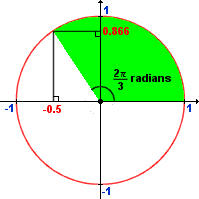
That would be absolutely amazing, if we only wanted a very small pie having just its lower-right quadrant visible, with pie slices that run "backwards" to the Western eye. Using our original chart as an example, we'll fix that little problem up in a jiffy. All we need to do is to determine how large the pie will be (its radius) and where its centre will lie on our SVG "page". In the example, we had a space of 400 by 400, and put the centre of the pie at the point (200,200) relative to the upper-left-hand corner. Then we made the radius of the pie 180 units, which gives us a little bit of "white space" around the pie.
Scaling the pie is easy. Since we want a radius of 180, and the values we calculated were for an imaginary circle of radius 1, we simply multiply the sine and cosine values we already calculated by 180. That makes the "pie" the right size, but it is still centred at (0,0), which is the upper-left-hand corner of the SVG space (with a defaultviewbox), and the slice would still be backwards if we drew it using these values.
An interesting thing happens, though, when we take our desired centre into account. When we subtract the new "scaled" values from the centre coordinates, up is still up (since subtracting positive values will leave us a "less down" value than the centre value, and subtracting negatives will give "more down"), but the pie is flipped left-to-right, and the order of the slices we build will be clockwise.
Let's build our first slice, then. First, we have to create the SVG space for the slice to live in:
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="400" height="400">
Now we need to draw the slice in the space. We'll use a <path>, as discussed above. The first step is to move the "pen" to the centre of the pie (<path d="M200,200"/>). Then we'll draw a line out from the centre to an arbitrary starting point 180 units directly to the left of the pie's centre (<path d="M200,200 L20,200"/>). Now to find the point to arc to.
The horizontal (or "x") component is arrived at by multiplying the cosine value we calculated earlier by the radius, 180, then subtracting the lot from the centre value, 200, leaving us with 290 (or 200 - (-0.5*180)). The vertical ("y") component uses the sine value in the same way, giving us 44.12 (or 200 - (0.866*180)). Since we know we are drawing a circle, both of the radius values will be the same, 180. We also know that one-third is less than one-half (so we won't need to set the long arc flag to 1), and that we want to proceed clockwise (so we do need the direction flag set to 1), so our path becomes (<path d="M200,200 L20,200 A180,180 0 0,1 290,44.12"/>). Adding a "Z" to bring us back to the centre will leave us with a black solid wedge of the appropriate size and shape (<path d="M200,200 L20,200 A180,180 0 0,1 290,44.12 Z"/>). Functional, but not very pretty — and if all of our slices are solid black, the chart will be less than useful.
The final step to this slice, then, will be to give it some character and distinction with some style attributes. Let's make it green with a two-unit black outline. That will finally give us:
<path d="M200,200 L20,200 A180,180 0 0,1 290,44.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/>
Don't forget to close off the SVG document or it won't render (SVG isn't forgiving of unclosed tags). That makes the whole SVG document:
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="400" height="400"> <path d="M200,200 L20,200 A180,180 0 0,1 290,44.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> </svg>
Still Hungry?
Of course, one slice does not a pie make — but before you get carried away creating all your slices the way we've done it so far, think about what will happen. All of the slices will start at the zero point, and stop somewhere clockwise of that point. Unless you only have one massive slice, you'll never get a pie out of the deal.
So howdowe bake a pie? The trick is to base our calculations on a running total rather than simply using the slice we are currently trying to create.
Let's say that our first slice represented 8,000 out of a total of 24,000. That still works out to one-third, so we can keep the calculations we've already made. What if our second slice was supposed to represent 6,000? We can't simply use 6,000 to calculate the arcTo point for this slice, but if we add it to the 8,000 we've already accounted for, that gives us a running total of 14,000. Now when we do the maths, we will be looking at a total angle of (14000/24000)*2πradians.
After much calculation (and I trust you are doing the calculations so you can plan your agent), I can almost hear you mutter, "Oh, great! Now we're going to completely obliterate the first slice!" Yes, Grasshopper, you would — if you started at the zero point again. Luckily, though, you remembered to keep track of the arcTo point in the first slice's path. When we create our path this time, we'll use the previous arcTo point as our lineTo point. Oh, and let's use a different colour while we're at it, since it would be nice to be able to tell the two slices apart.
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="400" height="400"> <path d="M200,200 L20,200 A180,180 0 0,1 290,44.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> <path d="M200,200 L290,44.12 A180,180 0 0,1 355.88,290 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/> </svg>
Now, if the next slice represents 4,000, it will give us a running total of 18,000, making our pie look like this:
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="400" height="400"> <path d="M200,200 L20,200 A180,180 0 0,1 290,44.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> <path d="M200,200 L290,44.12 A180,180 0 0,1 355.88,290 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/> <path d="M200,200 L355.88,290 A180,180 0 0,1 200,380 Z" style="fill: #0000ff; stroke: black; stroke-width: 2"/> </svg>
Now, let's say that in this case we have only one more slice to go. There is absolutely no need to calculate anything to create the last slice of the pie. Since the lineTo point of all slices except the first is the arcTo point of the previous slice, and we know that the pie has to end exactly where it started, we can simply go ahead and create the slice from data we already have:
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="400" height="400"> <path d="M200,200 L20,200 A180,180 0 0,1 290,44.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> <path d="M200,200 L290,44.12 A180,180 0 0,1 355.88,290 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/> <path d="M200,200 L355.88,290 A180,180 0 0,1 200,380 Z" style="fill: #0000ff; stroke: black; stroke-width: 2"/> <path d="M200,200 L200,380 A180,180 0 0,1 20,200 Z" style="fill: #ff00ff; stroke: black; stroke-width: 2"/> </svg>
As charts go, that's fairly usable. Just needs a bit of sprucing up is all. First, let's throw a drop-shadow under it. Rather than mucking about with pie slices (since we know what the whole pie will look like), we can just create the shadow as a blurred circle. A bit of a warning here, though: as simple as this is, the mere fact that we are using a Gaussian Blur filter to create the shadow will add considerably to the render time, even if the download time is virtually unaffected. Keep that in mind before you decide to use the shadow in a production environment, especially if you know you will be dealing with clients who may be using older, slower computers.
Note that we are creating the shadow first by drawing a solid circle and applying a basic Gaussian Blur filter (found in the defs section and referenced by URL in the circle's style attributes). That's because SVG renders items in the order they appear in the source. If we had saved the shadow till last, it would appear on top of the pie rather than "behind" and would obscure the chart.
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="400" height="400"> <defs> <filter id="dropshadow" width="120%" height="120%"> <feGaussianBlur stdDeviation="4"/> </filter> </defs> <circle cx="205" cy="205" r="180" style="fill: black; fill-opacity:0.6; stroke:none; filter:url(#dropshadow)"/> <path d="M200,200 L20,200 A180,180 0 0,1 290,44.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> <path d="M200,200 L290,44.12 A180,180 0 0,1 355.88,290 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/> <path d="M200,200 L355.88,290 A180,180 0 0,1 200,380 Z" style="fill: #0000ff; stroke: black; stroke-width: 2"/> <path d="M200,200 L200,380 A180,180 0 0,1 20,200 Z" style="fill: #ff00ff; stroke: black; stroke-width: 2"/> </svg>
That's prettier, alright, but we still haven't given any meaning to the data we are displaying. We need some labels. Unfortunately, it isn't really practical to try labelling the slices directly. It would be far too much trouble to figure out where to put the label text, and to avoid "collisions" between labels. A far more practical approach would be to use a colour-keyed legend elsewhere on the SVG page. The actual layout is up to you and the look and feel you are trying to achieve. In any case, it means making the SVG area substantially bigger than the chart area itself to leave enough room for the labels you require.
In this example, we'll make use of the <rect> (rectangle) element to create the colour swatches and the <text> element to create both the chart title and the label text in the legend. To make room for the title text, we are going to move the centre of the pie down by 100, and we will make the whole SVG space 800 wide to make room for the legend on the right-hand side.
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="800" height="500"> <defs> <filter id="dropshadow" width="120%" height="120%"> <feGaussianBlur stdDeviation="4"/> </filter> </defs> <text x="150" y="50" style="font-family: verdana, arial, sans-serif; font-size: 36; font-weight: bold; fill: #0099ff; stroke: black; stroke-width: 1"> A Pretty-As-Pie Chart </text> <circle cx="205" cy="305" r="180" style="fill: black; fill-opacity:0.6; stroke:none; filter:url(#dropshadow)"/> <path d="M200,300 L20,300 A180,180 0 0,1 290,144.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> <path d="M200,300 L290,144.12 A180,180 0 0,1 355.88,390 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/> <path d="M200,300 L355.88,390 A180,180 0 0,1 200,480 Z" style="fill: #0000ff; stroke: black; stroke-width: 2"/> <path d="M200,300 L200,480 A180,180 0 0,1 20,300 Z" style="fill: #ff00ff; stroke: black; stroke-width: 2"/> <rect x="420" y="140" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #00ff00"/> <text x="470" y="156" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The First Data Set - 33.3% </text> <rect x="420" y="180" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #ff0000"/> <text x="470" y="196" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Second Data Set - 25% </text> <rect x="420" y="220" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #0000ff"/> <text x="470" y="236" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Third Data Set - 16.7% </text> <rect x="420" y="260" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #ff00ff"/> <text x="470" y="276" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Fourth Data Set - 25% </text> </svg>
There's a lot more you can add to this yet, like mouseover effects. You can have the appropriate pie slice cause a legend entry to be highlighted on mouseover of either element if you like, or you can have a separate details pane pop up. I tend not use use mouseovers in SVG because of the lag between mouseover/mouseout and the change in the image. Again, the fault there lies with the current crop of SVG viewers. When performance improves, I will happily return to using mouseovers.
If you use different radii in the x- and y-axes, both as multipliers when you do your calculations and as arguments in the path statements, you can create an elliptical chart in perspective. Echoing the arcs in reverse below the main chart will allow you to create the illusion of a cylinder. Ruediger Seiffert's public-accesssample agentshows good examples of both of these techniques in use. It also uses mouseover effects. Like any other SVG, you can view the source code for the graphic to see what makes it tick.
Getting Tipsy
A top-on pie chart is more than adequate to display data, and it isthecanonical pie chart. Still, people have come to expect a 3-D look from "professional" charting utilities. If you are presenting the chart for public consumption, you might want to consider going to the trouble of a perspective rendering. A warning here, though — the distortion of the relationship between the areas of the various slices might not be acceptable in a strict statistical implementation. If you want to use a pie chart in a professional (web) publication, either stick to the top-on display or alter your calculations to render strict area proportions. (Thatishigher maths, and we won't be getting anywhere near that subject here.)
Slanting the top of the chart is no trouble at all. Let's take another look at the path statement for our first slice:
<path d="M200,300 L20,300 A180,180 0 0,1 290,144.12 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/>
Notice that there are two radii declared for the arcTo portion (A180,180 0 0,1 290,144.12). The arcTo is elliptical, after all — we've just used the same radius twice to create a circular shape. To create a perspective effect, we'll just use a smaller value for the y-radius (the second value). We can make the value as large or as small as we want, but there is a fairly small "band" of values that look right. Too large, and the chart won't appear tilted; too small, and the data represented won't be clear enough. I usually use a value two-thirds of the horizontal radius. In this case, that would be 120, making the arcTo portion "A180,120 0 0,1 290,144.12".
That leaves us with two problems. The first is that the point (290,144.12) will not lie on the ellipse we are trying to display. You'll get an arc alright, but it won't be the one you want. Remember that we got the y-value (144.12) by multiplying the sine of the angle by 180 and subtracting from 300 (the chart with labels has a 100-high area at the top for the title). We have to change the multiplier to 120 in order to put the point on the right ellipse. That will make our arcTo "A180,120 0 0,1 290,196.08"
I mentioned two problems. The one that remains is that since we've changed the y-radius to 120, the top of the ellipse now sits 60 units lower on the SVG space than our circle used to sit. White space is a good thing, but there is a difference between white space and a great gaping hole in your graphic. We can fix this by moving the centre of the ellipse up by the appropriate amount. That will make our chart look like this:
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="800" height="500"> <defs> <filter id="dropshadow" width="120%" height="120%"> <feGaussianBlur stdDeviation="4"/> </filter> </defs> <text x="150" y="50" style="font-family: verdana, arial, sans-serif; font-size: 36; font-weight: bold; fill: #0099ff; stroke: black; stroke-width: 1"> A Pretty-As-Pie Chart </text> <ellipse cx="205" cy="245" rx="180" ry="120" style="fill: black; fill-opacity:0.6; stroke:none; filter:url(#dropshadow)"/> <path d="M200,240 L20,240 A180,120 0 0,1 290,136.08 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> <path d="M200,240 L290,136.08 A180,120 0 0,1 355.88,300 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/> <path d="M200,240 L355.88,300 A180,120 0 0,1 200,360 Z" style="fill: #0000ff; stroke: black; stroke-width: 2"/> <path d="M200,240 L200,360 A180,120 0 0,1 20,240 Z" style="fill: #ff00ff; stroke: black; stroke-width: 2"/> <rect x="420" y="140" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #00ff00"/> <text x="470" y="156" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The First Data Set - 33.3% </text> <rect x="420" y="180" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #ff0000"/> <text x="470" y="196" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Second Data Set - 25% </text> <rect x="420" y="220" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #0000ff"/> <text x="470" y="236" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Third Data Set - 16.7% </text> <rect x="420" y="260" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #ff00ff"/> <text x="470" y="276" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Fourth Data Set - 25% </text> </svg>
That's gotten us a squashed pie chart, but it's not quite 3-D yet. It will let you see the kind of data distortion I was talking about, though. The 3-D touches we will add will provide some relief, but the distortion in the top surface will remain. (For those of you who absolutely need to fudge your data, putting the "good news" data at the left and right and the "bad news" data at the top and bottom will make your bosses day a little brighter.)
Notice that we've changed the element that creates the shadow from a circle to an ellipse. Apart from having different radii in the x and y directions, they are pretty much the same.
To complete the 3-D effect, we need to create the side of the cylinder. We'll do this by determining first which of our slices are at the front of the pie. Not only is there much point in drawing the back, we also have to keep in mind the painting order in SVG. That which comes first will be obliterated by later elements. There's also the problem of actually creating the shapes we need.
Finding the "front slices" is mathematically easy. We are looking for the first path that has a y-value in its arcTo that is greater than the y-value of the ellipse's centre. That, and all subsequent slices, will be at least partially at the front side of the cylinder. In the example, that slice would be the second one:
<path d="M200,240 L290,136.08 A180,120 0 0,1 355.88,300 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/>
As is usual for the first "front" slice, it does not lie entirely below the centre of the ellipse. The representation of the side of the cylinder, though, can only use what's below the centre. Not a problem — we know where the centre point of the right-hand side of our pie lives. It is a point even with the centre in the y direction and 180 to the right of centre in the x direction: (380,240).
We start building the new shape, a path, by repeating the curve of the slice to which it corresponds. The starting point for this curve will be the extreme right side of the pie, and the curve will end at the same point the slice's arcTo ends. That gives us:
<path d="M380,240 A180,120 0 0,1 355.88,300"/>
Now, to add some thickness to the cylinder, we simply drop down a bit and repeat the curve, then close the shape. How thick you want the cylinder to appear is up to you. I'll use 100 units in this example, although 100 is probably too much for the size of the chart. It's just easy to work with in my wee noggin — your agent won't have to worry about things like that. Dropping down gives us:
<path d="M380,240 A180,120 0 0,1 355.88,300 L355.88,400"/>
Now to repeat the curve. Remember that we're going anticlockwise this time (since the "pen" never lifts), so we need to set the direction flag to zero. Our end point will be 100 units below the point where the original curve started. We'll also close the shape using Z:
<path d="M380,240 A180,120 0 0,1 355.88,300 L355.88,400 A180,120 0 0,0 380,340 Z"/>
Each of the rest of the cylinder side pieces will start where the arc of the corresponding slice starts, but the construction proceeds in the same way. The style for each of these cylinder pieces should give a fill colour of roughly the same hue as the pie slice it goes with, but a little lighter or darker (again, up to your taste). If you want to use a drop shadow for the completed cylinder, you'll need to use a path to make it look right (elliptical arcs of slightly different sizes top and bottom joined by moderately diagonal lines). You'll probably find that the shadow can be dispensed with, and with it goes the performance-robbing Gaussian Blur filter. Without the shadow, the completed cylinder will look like this:
<?xml version="1.0" standalone="no" ?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.0//EN" "http://www.w3.org/TR/2001/PR-SVG-20010719/DTD/svg10.dtd"> <svg width="800" height="500"> <text x="150" y="50" style="font-family: verdana, arial, sans-serif; font-size: 36; font-weight: bold; fill: #0099ff; stroke: black; stroke-width: 1"> A Pretty-As-Pie Chart </text> <path d="M200,240 L20,240 A180,120 0 0,1 290,136.08 Z" style="fill: #00ff00; stroke: black; stroke-width: 2"/> <path d="M200,240 L290,136.08 A180,120 0 0,1 355.88,300 Z" style="fill: #ff0000; stroke: black; stroke-width: 2"/> <path d="M380,240 A180,120 0 0,1 355.88,300 L355.88,400 A180,120 0 0,0 380,340 Z" style="fill: #ff6666; stroke: black; stroke-width: 2"/> <path d="M200,240 L355.88,300 A180,120 0 0,1 200,360 Z" style="fill: #0000ff; stroke: black; stroke-width: 2"/> <path d="M355.88,300 A180,120 0 0,1 200,360 L200,460 A180,120 0 0,0 355.88,400 Z" style="fill: #6666ff; stroke: black; stroke-width: 2"/> <path d="M200,240 L200,360 A180,120 0 0,1 20,240 Z" style="fill: #ff00ff; stroke: black; stroke-width: 2"/> <path d="M200,360 A180,120 0 0,1 20,240 L20,340 A180,120 0 0,0 200,460 Z" style="fill: #ff66ff; stroke: black; stroke-width: 2"/> <rect x="420" y="140" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #00ff00"/> <text x="470" y="156" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The First Data Set - 33.3% </text> <rect x="420" y="180" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #ff0000"/> <text x="470" y="196" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Second Data Set - 25% </text> <rect x="420" y="220" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #0000ff"/> <text x="470" y="236" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Third Data Set - 16.7% </text> <rect x="420" y="260" width="30" height="20" style="stroke-linejoin: mitre; stroke-width: 2; stroke: black; fill: #ff00ff"/> <text x="470" y="276" style="font-family:verdana, arial, sans-serif; font-size: 14; fill: black; stroke: none"> The Fourth Data Set - 25% </text> </svg>
S is for Scalable
I can hear it already. "800 by 500? Are you out of your cotton-pickin' mind? I don't have room for that!"
Youcouldbuild the graphic smaller if you wanted to — but there's no need to. Remember that these are Scalable Vector Graphics. Scalable means that we can change the size of the displayed image to meet our needs, and Vector means that we won't lose any resolution in the process. (Graphics means pictures, but if you needed help with that it's time to stop reading articles like this one.) It also means that the size of the coordinate space won't have an appreciable effect on the file size. (Adding an extra digit here and there does make the file bigger, but we're talking about the difference between 2100 bytes and 2200 bytes for a ten-times increase in the overall coordinate system. If 100 bytes will really be a show-stopper, don't use any pictures at all.) Changing the size of the SVG on your web page doesn't have the same kind of implications that resizing a GIF or JPEG would have.
Earlier on, I mentioned the concept of theviewbox. The viewbox is the magical property that allows us to separate the external visible dimensions of the graphic (the size at which it displays) from the internal coordinate space (the fixed units we need to use to describe the shapes and positions of things). Changing one line in the SVG document will allow us to keep the nice, roomy 800 by 500 layout space while displaying the resulting graphic at any size we want. Simply change:
<svg width="800" height="500">
to make it read:
<svg width="100%" height="100%" viewBox="0 0 800 500" preserveAspectRatio="xMidYMax meet">
Setting the width and height to 100% now means that the graphic will take up as much room as you allow it to on your web page. The viewBox parameters give the upper-left and bottom-right corners of the displayed coordinate space. In this case we're telling the graphic to display everything in the original 800 by 500 coordinate space at whatever size is allowed. The preserveAspectRatio setting keeps the pie round. Without this, the graphic would distort to fit the space available. Telling it to preserve the aspect ratio keeps everything in proportion, so whichever measure (available width or available height) is most limiting will control the overall size of the display. The actual setting will depend on where the image is positioned on your page, and how you want it to shrink and grow. The setting given here (xMidYMax meet) is best for an image that is centred horizontally.
If the display area for the SVG on the web page is set in percentages (say it's centred with a width of 80%), the graphic will display at different sizes on monitors with different resolutions. It will also resize as the browser window is resized. Something like this will do quite nicely:
<html> <head> <title>Embedded SVG Test</title> </head> <body> Some text above <center> <embed src="pie.svg" width="80%" height="80%" type="image/svg+xml"> </center> Some text below </body> </html>
So, as it turns out, youcandesign a graphically-rich web page for more than one "optimum" resolution. Cool?
 Stan Rogers is an analyst withGroupe CGI Ltée, a worldwide IT consultancy based in Canada. He has been working with Lotus Notes and Domino for a little less than two years. Trained as an electronics technologist, and working for several years as an educator, his computing skills are mostly self-taught -- with a lot of help from sites like this.
Stan Rogers is an analyst withGroupe CGI Ltée, a worldwide IT consultancy based in Canada. He has been working with Lotus Notes and Domino for a little less than two years. Trained as an electronics technologist, and working for several years as an educator, his computing skills are mostly self-taught -- with a lot of help from sites like this.
http://www.codestore.net/store.nsf/unid/epsd-5dtt4l
最后
以上就是合适小懒猪最近收集整理的关于如何用纯HTML5画SVG饼图pie chart的全部内容,更多相关如何用纯HTML5画SVG饼图pie内容请搜索靠谱客的其他文章。








发表评论 取消回复