主要内容摘抄自 https://zhuanlan.zhihu.com/p/24309547
感谢大大。
# -*- coding: utf-8 -*-
# __author__ = 'wangxuhao'
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# 通过rcParams设置全局横纵轴字体大小
mpl.rcParams['xtick.labelsize'] = 24
mpl.rcParams['ytick.labelsize'] = 24
np.random.seed(42)
# x轴的采样点
x = np.linspace(0, 5, 100)
# 通过下面曲线加上噪声生成数据,所以拟合模型就用y了……
y = 2*np.sin(x) + 0.3*x**2
y_data = y + np.random.normal(scale=0.3, size=100)
# figure()指定图表名称
plt.figure('data')
# '.'标明画散点图,每个散点的形状是个圆
plt.plot(x, y_data, '.')
# 画模型的图,plot函数默认画连线图
plt.figure('model')
plt.plot(x, y)
# 两个图画一起
plt.figure('data & model')
# 通过'k'指定线的颜色,lw指定线的宽度
# 第三个参数除了颜色也可以指定线形,比如'r--'表示红色虚线
# 更多属性可以参考官网:http://matplotlib.org/api/pyplot_api.html
plt.plot(x, y, 'k', lw=3)
# scatter可以更容易地生成散点图
plt.scatter(x, y_data)
# 一定要加上这句才能让画好的图显示在屏幕上
plt.show()
# -*- coding: utf-8 -*-
# __author__ = 'wangxuhao'
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['axes.titlesize'] = 20
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
mpl.rcParams['axes.labelsize'] = 16
mpl.rcParams['xtick.major.size'] = 0
mpl.rcParams['ytick.major.size'] = 0
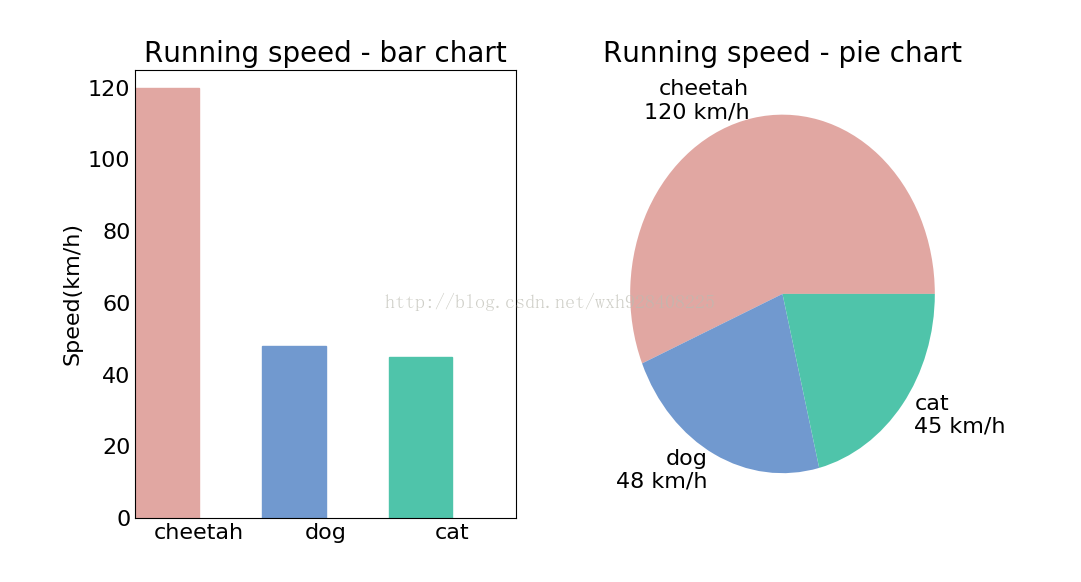
# 包含了狗,猫和猎豹的最高奔跑速度,还有对应的可视化颜色
speed_map = {
'dog': (48, '#7199cf'),
'cat': (45, '#4fc4aa'),
'cheetah': (120, '#e1a7a2')
}
# 整体图的标题
fig = plt.figure('Bar chart & Pie chart')
# 在整张图上加入一个子图,121的意思是在一个1行2列的子图中的第一张
ax = fig.add_subplot(121)
ax.set_title('Running speed - bar chart')
# 生成x轴每个元素的位置
xticks = np.arange(3)
# 定义柱状图每个柱的宽度
bar_width = 0.5
# 动物名称
animals = speed_map.keys()
# 奔跑速度
speeds = [x[0] for x in speed_map.values()]
# 对应颜色
colors = [x[1] for x in speed_map.values()]
# 画柱状图,横轴是动物标签的位置,纵轴是速度,定义柱的宽度,同时设置柱的边缘为透明
bars = ax.bar(xticks, speeds, width=bar_width, edgecolor='none')
# 设置y轴的标题
ax.set_ylabel('Speed(km/h)')
# x轴每个标签的具体位置,设置为每个柱的中央
ax.set_xticks(xticks+bar_width/2)
# 设置每个标签的名字
ax.set_xticklabels(animals)
# 设置x轴的范围
ax.set_xlim([bar_width/2-0.5, 3-bar_width/2])
# 设置y轴的范围
ax.set_ylim([0, 125])
# 给每个bar分配指定的颜色
for bar, color in zip(bars, colors):
bar.set_color(color)
# 在122位置加入新的图
ax = fig.add_subplot(122)
ax.set_title('Running speed - pie chart')
# 生成同时包含名称和速度的标签
labels = ['{}n{} km/h'.format(animal, speed) for animal, speed in zip(animals, speeds)]
# 画饼状图,并指定标签和对应颜色
ax.pie(speeds, labels=labels, colors=colors)
plt.show()
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
# 3D图标必须的模块,project='3d'的定义
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
n_grids = 51 # x-y平面的格点数
c = n_grids / 2 # 中心位置
nf = 2 # 低频成分的个数
# 生成格点
x = np.linspace(0, 1, n_grids)
y = np.linspace(0, 1, n_grids)
# x和y是长度为n_grids的array
# meshgrid会把x和y组合成n_grids*n_grids的array,X和Y对应位置就是所有格点的坐标
X, Y = np.meshgrid(x, y)
# 生成一个0值的傅里叶谱
spectrum = np.zeros((n_grids, n_grids), dtype=np.complex)
# 生成一段噪音,长度是(2*nf+1)**2/2
noise = [np.complex(x, y) for x, y in np.random.uniform(-1,1,((2*nf+1)**2/2, 2))]
# 傅里叶频谱的每一项和其共轭关于中心对称
noisy_block = np.concatenate((noise, [0j], np.conjugate(noise[::-1])))
# 将生成的频谱作为低频成分
spectrum[c-nf:c+nf+1, c-nf:c+nf+1] = noisy_block.reshape((2*nf+1, 2*nf+1))
# 进行反傅里叶变换
Z = np.real(np.fft.ifft2(np.fft.ifftshift(spectrum)))
# 创建图表
fig = plt.figure('3D surface & wire')
# 第一个子图,surface图
ax = fig.add_subplot(1, 2, 1, projection='3d')
# alpha定义透明度,cmap是color map
# rstride和cstride是两个方向上的采样,越小越精细,lw是线宽
ax.plot_surface(X, Y, Z, alpha=0.7, cmap='jet', rstride=1, cstride=1, lw=0)
# 第二个子图,网线图
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_wireframe(X, Y, Z, rstride=3, cstride=3, lw=0.5)
plt.show()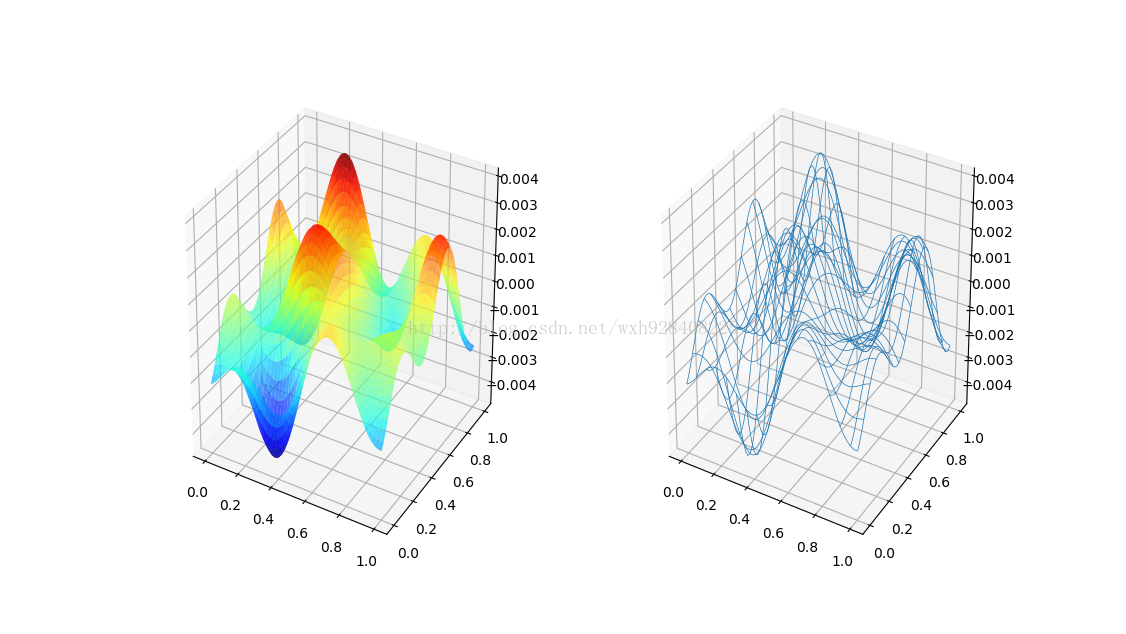
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
# 采样个数500
n_samples = 500
dim = 3
# 先生成一组3维正态分布数据,数据方向完全随机
samples = np.random.multivariate_normal(
np.zeros(dim),
np.eye(dim),
n_samples
)
# 通过把每个样本到原点距离和均匀分布吻合得到球体内均匀分布的样本
for i in range(samples.shape[0]):
r = np.power(np.random.random(), 1.0/3.0)
samples[i] *= r / np.linalg.norm(samples[i])
upper_samples = []
lower_samples = []
for x, y, z in samples:
# 3x+2y-z=1作为判别平面
if z > 3*x + 2*y - 1:
upper_samples.append((x, y, z))
else:
lower_samples.append((x, y, z))
fig = plt.figure('3D scatter plot')
ax = fig.add_subplot(111, projection='3d')
uppers = np.array(upper_samples)
lowers = np.array(lower_samples)
# 用不同颜色不同形状的图标表示平面上下的样本
# 判别平面上半部分为红色圆点,下半部分为绿色三角
ax.scatter(uppers[:, 0], uppers[:, 1], uppers[:, 2], c='r', marker='o')
ax.scatter(lowers[:, 0], lowers[:, 1], lowers[:, 2], c='g', marker='^')
plt.show()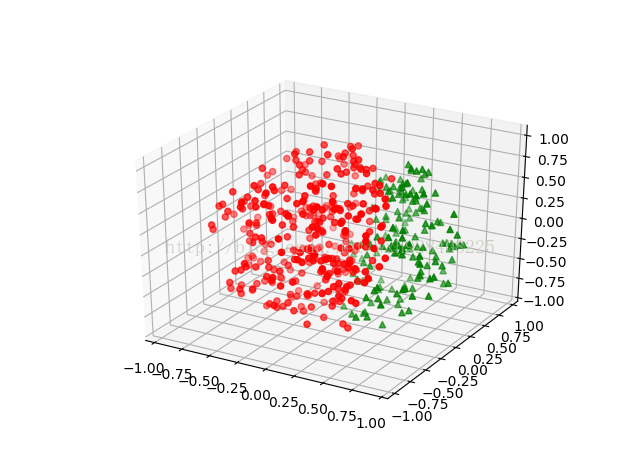
最后
以上就是诚心大象最近收集整理的关于python Matplotlib 学习笔记(2)的全部内容,更多相关python内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复