matlibplot 一张图画多个曲线_Hilbert曲线在基因组数据可视化中的应用

今天我既不介绍怎么画圆，也不介绍怎么画方。今天我介绍的是怎么画线。

Hilbert曲线(https://en.wikipedia.org/wiki/Hilbert_curve)是一种空间填充曲线。它把一条一维空间的线条在二维空间中按照某种特定的方式进行折叠。它的一个特有的性质是：如果两个点在一维线条上距离相近的话，那么它们在二维折叠曲线上距离大致也会相近，也就是说，这种折叠方式保留了点与点之间的邻近性(locality)。

我们假设在一维线条上可以可视化个点，那么当扩展到二维空间后，可以可视化个点，因此，这大大提高了可视化的分辨率。比如说，在一维情形下，对基因组数据可视化的精度为1MB，那么在Hilbert曲线上，你可以得到1KB的精度！

今天的这篇文章介绍了我的一个Bioconductor包：HilbertCurve。它是受到如下文章或者工具的启发：

• http://mkweb.bcgsc.ca/hilbert/
• http://corte.si/posts/code/hilbert/portrait/index.html
• http://bioconductor.org/packages/devel/bioc/html/HilbertVis.html

HilbertCurve包可以非常简单的使用。因为理论上，它显示的是一个一维的数据(你不用管最终画出来的坐标轴是直的还是折叠过的)，用户只需要提供在一维空间中数据点的坐标和绘图方式(也就是画点还是画线，或者使用什么颜色)，最终map到Hilbert曲线上的操作由HilbertCurve包自动处理。

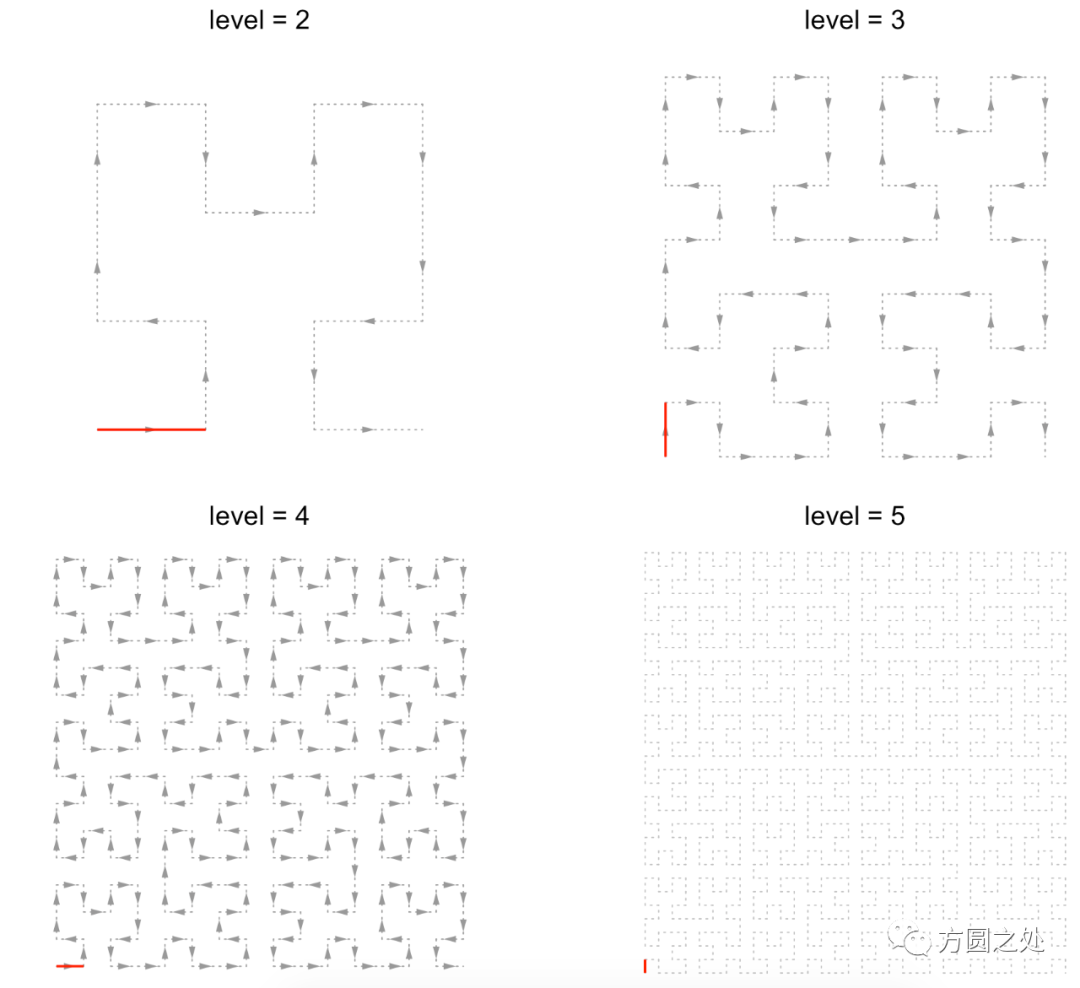
首先我们来看看Hilbert曲线长什么样子。Hilbert曲线需要一个参数(level)来控制折叠的程度。比如下图中我们显示了level为2，3，4和5的曲线，其中线段(下图中红色线段)的条数为4^level - 1或者有4^level个折点。因此当level为10时，Hilbert曲线将被折叠为1048575条线段。如果每条线段都能匹配上一个数据点，那么这条曲线将能可视化1048575个数据点！

Hilbert曲线将一条一维的线条进行折叠，下面这幅动图显示了数据点是如何在这条折叠了的曲线上(level为5)从最小值到最大值移动的。

我刚才说到Hilbert曲线保持了数据点在一维直线上的邻近性，下面我们计算了一条level为5的Hilbert曲线上平均分布的1024个折点在二维平面上的距离，显示在如下的热图中：

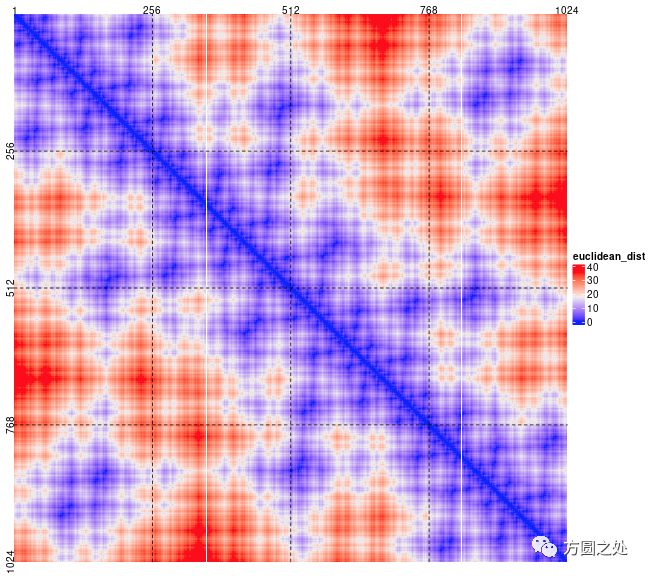
热图中的x轴(从左到右)和y轴(从上到下)表示曲线上第一个点到第1024个点，热图中第(i,j)个值表示第i个点与第j个点在二维平面上的距离。可见当i和j比较近似时，它们之间在二维平面上的距离也很相近(对角线上)。当然也有一些点i和j的差别较大，但是在二维平面上距离却很近(比如左下方蓝色区域)。这主要是曲线折叠造成的，但是这种情形很容易在最终的Hilbert曲线上区别开来，我会在下面的例子中展示。

如何使用HilbertCurve包

我下面介绍如何使用HilbertCurve包。正如我已经在前面说过，Hilbert曲线处理的还是一维空间的数据，因此，我们假想Hilbert曲线是作用到一个一维的坐标系中，那么，和常规的二维坐标系类似，我们只要确定坐标系的范围和图形的类型即可。

我们首先需要使用HilbertCurve()函数设定坐标系的范围以及曲线的level。然后使用低水平的绘图函数如hc_points() ，hc_rect()等在曲线上添加图形。最终，通过多种不同方式的低水平绘图函数的组合生成复杂的图形。

hc = HilbertCurve(...)    # 初始化曲线
hc_points(hc, ...)        # 添加点
hc_rect(hc, ...)          # 添加矩形
hc_polygon(hc, ...)       # 添加多边形
hc_segments(hc, ...)      # 添加线段
hc_text(hc, ...)          # 添加文字

下面是在一条leve为3的曲线上添加各种不同形状的点的例子。在这个例子中，Hilbert曲线上每一个线段用三个点切分，同时ir中所对应的每一个区间用一连串的点表示。

library(HilbertCurve)
library(IRanges)
hc = HilbertCurve(1, 100, level = 4, reference = TRUE)
x = sort(sample(100, 20))
s = x[1:10*2 - 1]
e = x[1:10*2]
ir = IRanges(s, e)
hc_points(hc, ir, np = 3, 
    gp = gpar(fill = rand_color(length(ir))),
    shape = sample(c("circle", "square", "triangle", 
        "hexagon", "star"), length(ir), replace = TRUE))

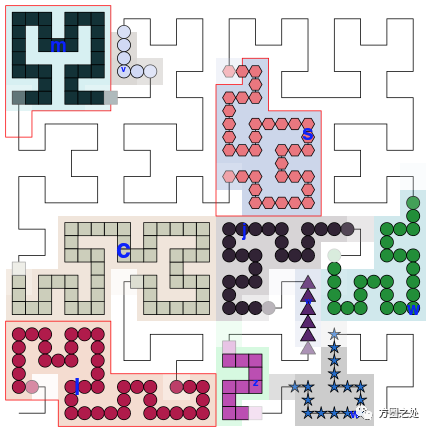
通过对各种低水平绘图函数的各种组合，可以生成复杂的图，如下所示：

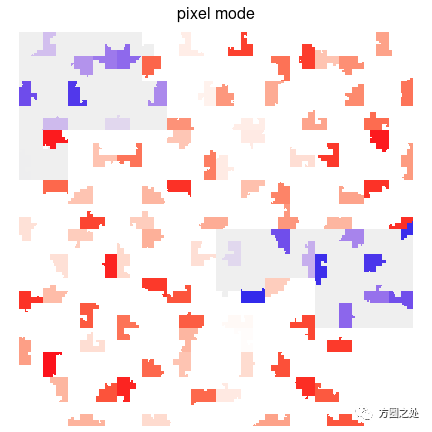
Pixel模式

当曲线的level越来越大时，比如10或者10以上，曲线会被切分成越来越多的线段，而每条线段在图形中会变得越来越小，以至于无法分辨。为了更有效率的显示曲线，HilbertCurve引进了一个“pixel模式“。在这个模式下，曲线上的折点或者线段退化为像素点，数据点只能用颜色来map。那么一个例如level为10的曲线将会用1024x1024的RGB点阵图表示。

hc_layer(...)

hc_layer()可以支持多个图层，下图中灰色区域覆盖的地方颜色模式被替换成了白色-蓝色。

更多的例子

下面我展示一些Hilbert曲线应用的有趣的例子。

第一个例子是颜色从红色到紫色按照彩虹色的顺序渐变。我用点来表示每个渐变的颜色(ht_points())。

第二个例子和第一个相似，但是这次我把矩形放到曲线中(hc_rect())。

第三个例子是全球IPv4地址的分布，因为IPv4的地址可以映射到一条直线上，因此Hilbert曲线是一个理想的可视化方式。

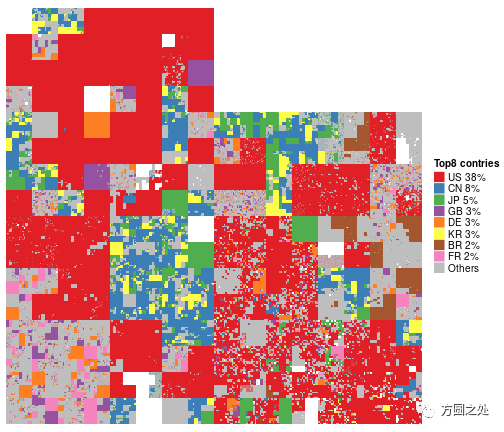
第四个例子是中国朝代时间线。我用线段的不同粗细和颜色来表示不同的朝代。春秋战国的持续时间是不是比你想象中要长？

处理基因组数据

好，前面纯属提起读者的兴趣，那么现在的问题是，对于我们分析和可视化基因组数据，Hilbert曲线有用么？基因组通常可以被视为一维的数据，从第一个碱基到最后一个碱基，而往往基因组会包含上百万至上十亿的碱基。这意味着基因组其实对应着一条很长的一维的坐标系，因此Hilbert曲线是一个很合适的可视化的方法。

我先展示三个在基因组数据中应用的例子。第一个是显示人第一条染色体中基因的分布。在下图中，基因用不同颜色表示。

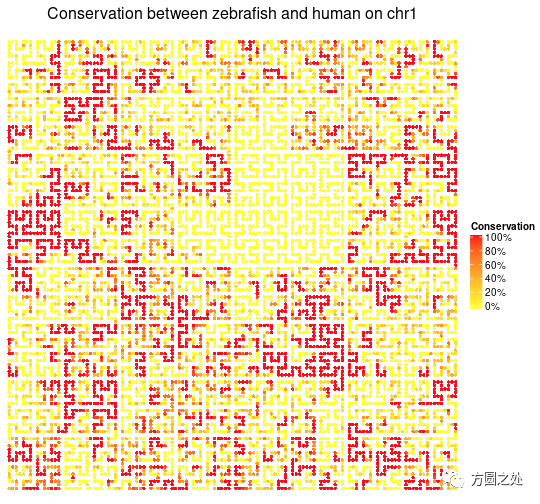
第二个例子是人和斑马鱼基因组序列相似性。

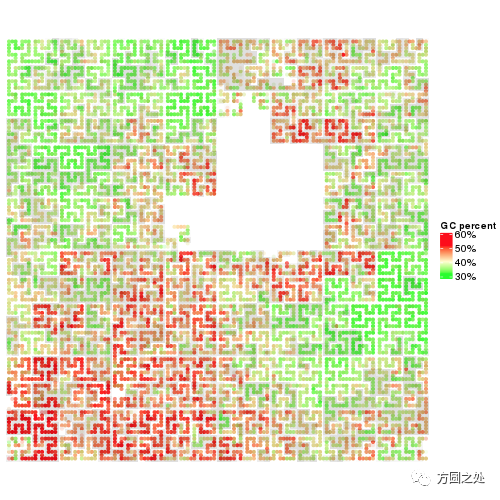
第三个例子是人第一条染色体中GC的含量。

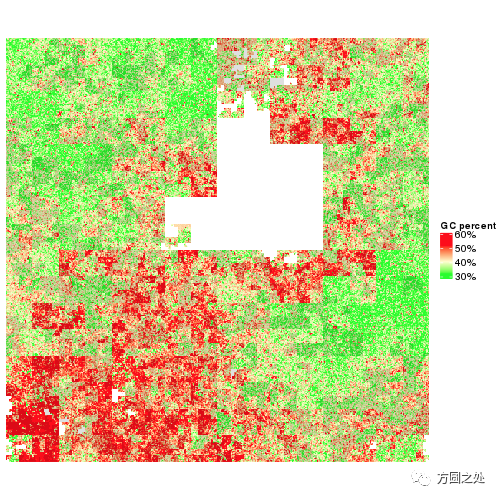
下一张图与上一张相同，也是表示GC含量，但是这是一条在pixel模式下的level为11的曲线。

好，到现在为止，读者可能会觉得Hilbert曲线的形式大于内容。它生成的图是非常特别，但是对于真正的基因组水平的数据分析，它究竟能带来什么优势，或者能够给我们提供别的方法所无法提供的信息吗？

这是一个好问题。回忆Hilbert曲线的两个特点：

1. 提供高分辨率的可视化；
2. 保留了数据点的邻近性。

因此，对于基因组数据来说，它能够非常有效率的可视化在基因组中大小为几kb的区域，同时它也能有效的呈现cluster的模式。

首先，我认为它能够很好的可视化ChIP-seq中不同的histone modification(组蛋白修饰)的信号。

在下面的图中，所有的Hilbert曲线都在pixel模式下绘制，其中包含了两个layer，一个是histone modification本身的强度(红色)，另一个表示了基因区域(灰色)。

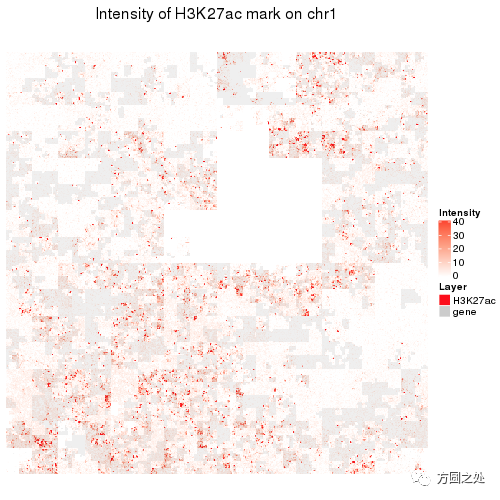
第一个是H3K27ac组蛋白修饰，这通常发生在active promoter和enhancer区域。我们可以看到在Hilbert曲线上，有很多特别小的点。这些都是H3K27ac的peak region。而且这些peak有呈现为cluster的趋势。

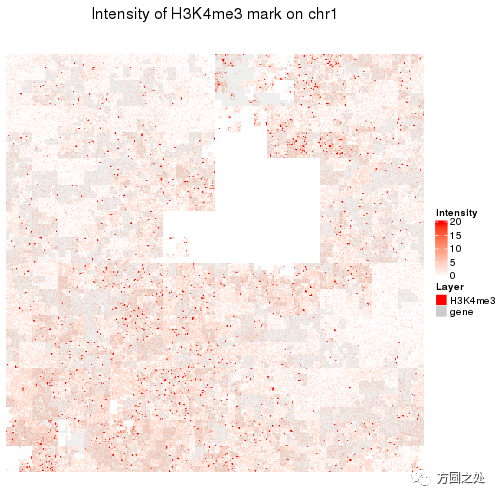
第二个是H3K4me3修饰，这是一个很强的active promoter的修饰。同样我们在曲线上看到特别多的点，但和H3K27ac相比，H3K4me3的区域更多，而且长度更短。基本观察不到cluster的模式。

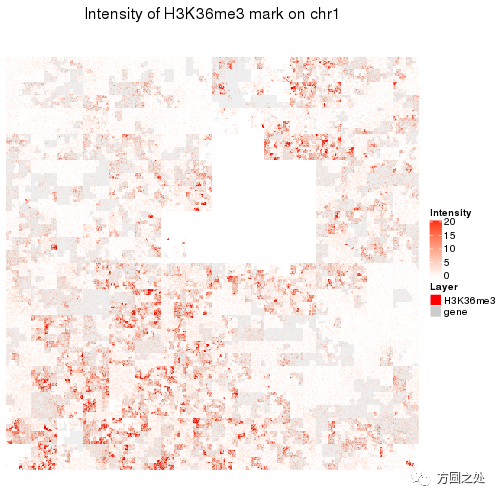
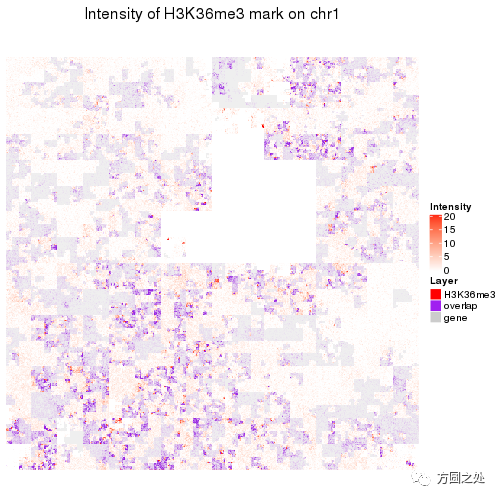
第三个是H3K36me3修饰，通常对应着actively transcribed gene body。

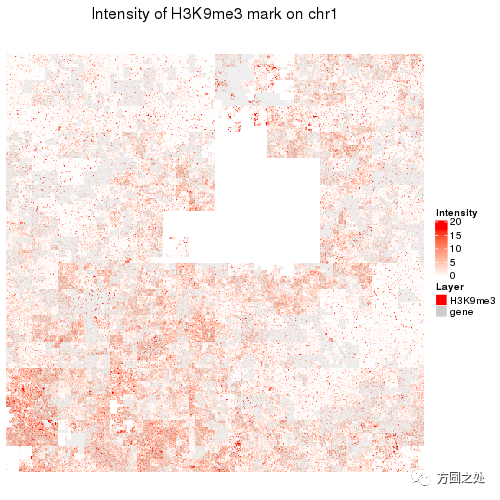
第四个是H3K9me3，通常对应着长范围的转录抑制调控。可以看到部分区域是非常非常长。而且在染色体的起始部分有富集。结合前面的一个例子，染色体起始部分GC含量更高，并且有更多的基因存在于那儿。

前面我说到H3K36me3对应的是active gene body，下面我将gene区域overlay到曲线上。在下图中，如果H3K36me3在基因区域中，颜色模式为白色-紫色，如果在基因区域外，颜色模式为白色-红色。下图完美的表现出H3K36me3的区域和基因高度重合。

其次，Hilbert曲线也可以适用于可视化基因组水平的甲基化。下图中我们可以看到有很多的蓝色的点。这些对应着CGI (CpG Island)，大部分在gene的promoter附近，在正常的细胞中，它们都是低甲基化的，同时有很多高甲基化的区域显示为红色。如果观察仔细的话，还有很多红色向白色变化的区域，这些区域的甲基化水平略为降低。同时红色和浅红色的区域都显示为block的特征，也就是说，在基因组中，一大段区域连续的为高甲基化，然后一大段的区域持续的为中等甲基化。在癌细胞中，在中等甲基化的区域，其甲基化水平会进一步的降低，而Hilbert曲线可以非常好的体现这一点。

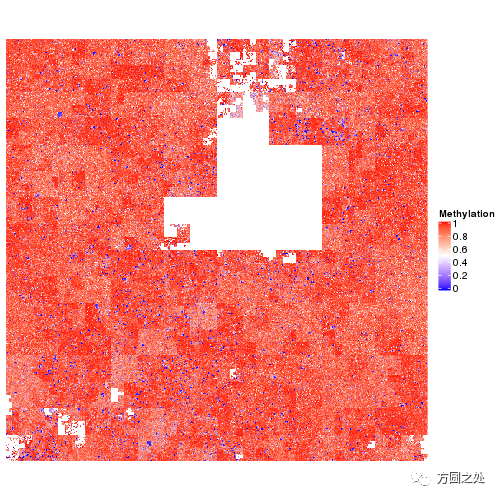
在甲基化数据分析中，我们常说，基因组水平的甲基化显示出bi-model的特点，即当计算基因组水平甲基化分布时，我们会在密度分布图上看到两个峰， 一个在低甲基区域，一个在高甲基化区域。Hilbert曲线进一步的展示出，低甲基化区域和高甲基化区域在基因组中是如何分布的。

前面我们显示了可视化一条染色体，HilbertCurve同样也可以将多条染色体map到曲线上。下图中包含了22条染色体，这是一个基因组范围的CNV的分布。

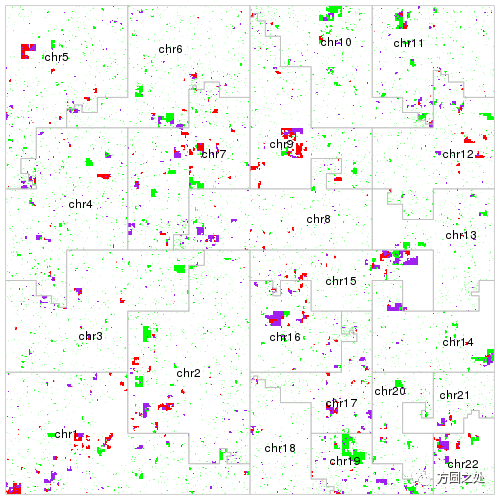
和普通的HilbertCurve类似，在初始化曲线时，我们需要GenomicHilbertCurve()函数指定使用哪些染色体，或者提供一个用户自定义的背景区域。然后根据用户提供的基因组数据(以GRanges对象的方式)使用低水平的绘图函数或者hc_layer()进行绘图。具体的关于HilbertCurve包的使用方法请见其文档。

hc = GenomicHilbertCurve(chr, species, ...)
hc = GenomicHilbertCurve(background, ...)

hc_points(hc, gr, ...)
hc_rect(hc, gr, ...)
hc_polygon(hc, gr, ...)
hc_segments(hc, gr, ...)
hc_text(hc, gr, ...)
hc_layer(hc, gr, ...)

结语

Hilbert曲线是一种非常特别的对基因组数据的可视化方式。你可能需要对Hilbert曲线有一些了解，才能很好的解读它，而当你理解Hilbert曲线并且作用到你的数据之后，你会惊讶于有如此精妙的方法，让你能够看到常规方法所无法展示的细节，同时给你艺术的美感。It makes your day.

往期文章：

• 多个组别的和弦图

• 绘制基因组水平的热图

• circlize中有趣的坐标系转换

• 从pheatmap无缝迁移至ComplexHeatmap

• 使用circlize绘制基因与pathway的关系图