目录

一、欧拉图

欧拉图与欧拉回路

欧拉图性质

Fleury算法找欧拉回路

二、哈密尔顿图

哈密尔顿图与哈密尔顿路（圈）

性质与判定

哈密尔顿图的性质定理

哈密尔顿图判定定理

闭图与闭包

 邦迪——闭包定理

度序列判定法

一、欧拉图

欧拉图与欧拉回路

对于只存在欧拉迹，不存在欧拉闭迹的图成为半欧拉图，欧拉图与半欧拉图都是连通图

欧拉图性质

对于半欧拉图，恰好有两个奇点

这种是常规操作，奇度点在图中一定有偶数个，只要我们将奇度点两两配对，一定可以将一个图变成欧拉图，比如这个例题，有8个奇度点，所以需要用4笔画完

因为n阶完全图每个顶点度数为n-1，n方体的度数就是n，完全二部图，a个顶点的部分，顶点的度数都是b，b个顶点的部分，顶点的度数都是a

只需要在两个连通分支之间添加一条重边即可，这样图中顶点的度数都是偶数

如果添加一条非重边，则正好产生两个奇度点，变成了半欧拉图

一定没有，割边一定不在圈之中，而对于欧拉图来说，边集可以看成是边不重合的圈的并，所以欧拉图中的每条边一定都在圈之中，即欧拉图中一定没有割边。

一共有C(2,7)+7=28种情况，即7中数字中选两个组合，再加上上下两部分点数相同的情况。

证明欧拉图有两点，一证明每个点的度都是偶数，二证明此图是连通图，可以通过证明任意两点间都有通路来说明。

上例说明，欧拉图的积图还是欧拉图

Fleury算法找欧拉回路

总结起来就是：除非万不得已，否则不走割边

二、哈密尔顿图

哈密尔顿图与哈密尔顿路（圈）

平凡图认为不是哈密尔顿图，则图中有G3,G5,G6三个哈密尔顿图，图G4虽然不存在哈密尔顿圈，但是存在哈密尔顿路，即不重复的包含所有顶点的路

性质与判定

哈密尔顿图的性质定理

哈密尔顿圈减去顶点集得到的连通分支数小于等于顶点集中顶点个数，哈密尔顿图包含圈，所以哈密尔顿图减去同一个顶点集得到的连通分支数一定小于等于圈减去顶点集得到的分支数，所以不等式传递，性质定理得以证明。

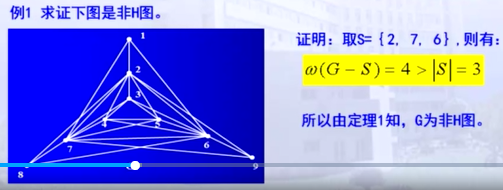
例题：对于偶图（n,m），它是哈密尔顿图的必要条件是n=m，因为若n与m不相等，则我们删去点少的那个部分，得到的全是单点，即全是单点构成的连通分支，连通分支数会大于减去点集合中的点数。

性质定理只是必要条件，满足条件不一定是哈密尔顿图，如反例，彼得森图

哈密尔顿图判定定理

判定定理1

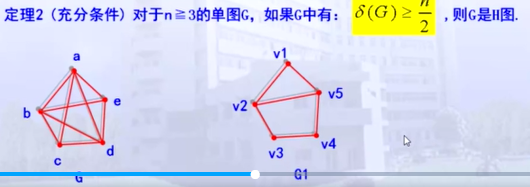
顶点数大于等于3，简单图，最小度大于等于顶点数的一半，则可判定是哈密尔顿图

判定定理2

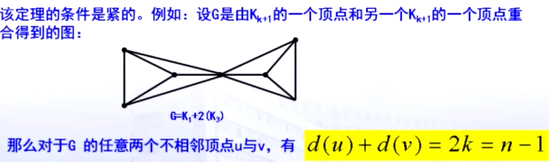
闭图与闭包

闭图

闭图定义，对于度数之和大于等于n的两个点，它们俩必须相邻。但是相邻的点度数之和不一定要大于等于n，如上边例子，G2是闭图，但是其中根本就没有度数之和大于等于n的一对顶点！！！

闭图的交仍然是闭图，闭图的并则不一定！

闭包

首先闭包一定是闭图！如果一个图不是闭图，它有不相邻点的度数之和大于等于n，则把这对不相邻点连线，直到所有度数之和大于等于n的点对都是相邻的，就完成了该图的闭包！

 邦迪——闭包定理

度序列判定法

最后

以上就是悦耳哈密瓜为你收集整理的图论（10）欧拉图与哈密尔顿图一、欧拉图二、哈密尔顿图的全部内容，希望文章能够帮你解决图论（10）欧拉图与哈密尔顿图一、欧拉图二、哈密尔顿图所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。