概述
前言
本章讨论图的最短路径问题
方法
1.概念
所谓图的最短路径，就是用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。日常生活中如高德地图、百度地图会有类似换乘少、路程短等导航推荐，就是基于图的最短路径。
2.最短路径类型
1）非加权图的最短路径
我们拿上个博客中的例子来看：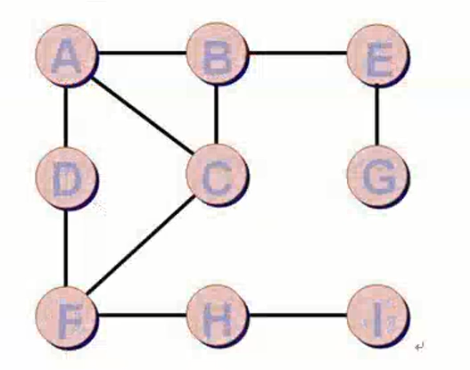
如果求A出发到G的最短路径怎么求呢?那么按照段数进行区别，段数越少代表最短路径。
也许，你可以从上面的图中一眼就看出来最短路径，当然这只是一个十分简单的图，一旦复杂起来，就需要借助相应的算法。
该算法类似于树的层次遍历，需要借助队列来实现。
- 首先将目标顶点A入队列。
- 当队列不为空时，执行循环：
- 顶点出队列，遍历该顶点的邻接表，更新它们距顶点的最短距离（无权图一段距离为1），更新它们的上一个结点。它们（该顶点的邻接点）入队列。
- 当队列为空时，遍历完A的所有可达顶点。可以得到到所有顶点的最短路径。
具体的算法过程我已经在资源中给出。
2）加权图的最短路径
求下面这个加权图的最短路径
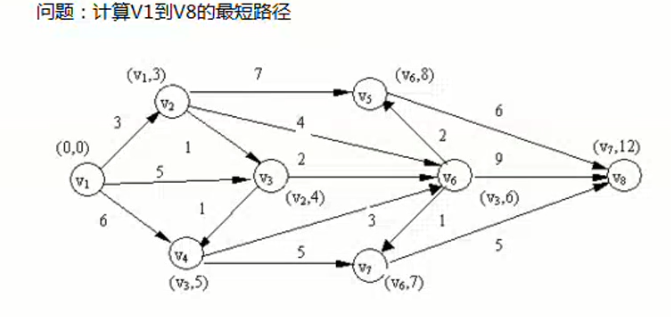
假设加权图的权代表结点间的距离，求v1到v8的最短路径。
要想解决该问题，我们需要使用狄克斯特拉算法（Dijkstra算法）来求解！
具体的算法过程我已经在资源中给出。
最后
以上就是高大店员为你收集整理的数据结构和算法（十一）图的最短路径前言方法的全部内容，希望文章能够帮你解决数据结构和算法（十一）图的最短路径前言方法所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复