求解图的最短路径的另一种方法：迪杰斯特拉算法(Dijkstra)

求解图的最短路径的方法有两种，其中迪杰斯特拉算法(Dijkstra)适合求图中一个顶点到其他顶点的最短路径，而弗洛依德算法(Floyd)适合求图中每一对顶点之间的最短路径。 如果使用Dijkstra求解，则需要循环地以图中的每个顶点都作为起点，一共使用n次算法，时间复杂度为O(n ^ 3)。使用弗洛依德算法(Floyd)的时间复杂度也是O(n ^ 3 )，但是形式上比较简单。

算法思路

弗洛依德算法(Floyd) 使用的是动态规划的思想，我们首先我们使用一个二维数组dist[][]来存储当前的最短路径，然后寻找一个顶点k，如果vi到k的长度和k到vj的长度比vi到vj的长度还要低，就把dist[vi][vj]更新为dist[vi][k] + dist[k][vj]。

代码

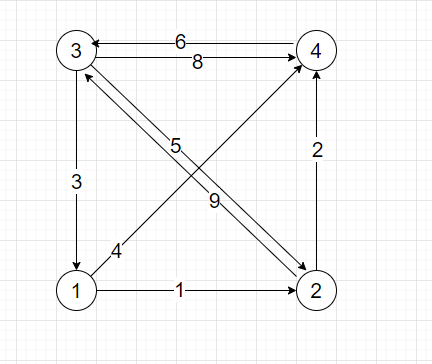
以下面的有向图为例：

/*
    最短路径：弗洛依德算法
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1024;   //最大顶点数
int n,m;  //顶点的个数，边的个数
int dist[maxn][maxn];   //dist[i][j] 记录顶点i到顶点j的最短路径长度
int matrix[maxn][maxn];   //邻接矩阵


/*
增加一条从v1指向v2的边，权值为k
*/
void link(int v1,int v2,int k){
    matrix[v1][v2] = k;
    //如果是无向图，则再加上matrix[v2][v1] = k;
}


/*
图的初始化
*/
void init(){
    //初始化邻接矩阵
    for(int i = 0;i<=maxn;++i){
        for(int j = 0;j<maxn;++j){
            matrix[i][j] = -1;
        }
    }
    n = 4;
    m = 8;
    //下面m行建图
    link(1,2,1);
    link(1,4,4);
    link(2,3,9);
    link(2,4,2);
    link(3,1,3);
    link(3,2,5);
    link(3,4,8);
    link(4,3,6);
}

/*
Floyd算法
*/
void floyd(){
    for(int i = 1;i <= n;++i){
        for(int j = 1;j<=n;++j){
            dist[i][j] = matrix[i][j];  //初始时，设置dist数组和matrix一样
            if(i == j){
                dist[i][j] = 0; //自己到自己的最短路径是0
            }
        }
    }


    for(int k = 1;k<=n;++k){
        for(int i = 1;i<=n;++i){
            for(int j = 1;j<=n;++j){
                if(dist[i][k] != -1/*i--k有计算过路径长度*/ && dist[k][j] != -1/*k--j有计算过路径长度*/ && (dist[i][k] + dist[k][j] < dist[i][j] || dist[i][j] == -1)/*新的路径长度比原来的小||原来没有计算过路径长度*/){
                    dist[i][j] = dist[i][k] + dist[k][j];
                }
            }
        }
    }

    /*
        输出最短路径
    */
    for(int i = 1;i<=n;++i){
        for(int j = 1;j<=n;++j){
            cout << i << " -- "<< j <<" : " << dist[i][j] << endl;
        }
    }
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	init();
    floyd();
	return 0;
}

运行结果

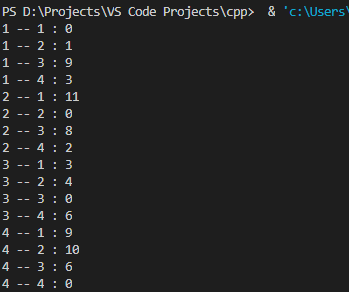
最后

以上就是孤独手套为你收集整理的（数据结构）图的最短路径 弗洛依德算法(Floyd)算法思路代码运行结果的全部内容，希望文章能够帮你解决（数据结构）图的最短路径 弗洛依德算法(Floyd)算法思路代码运行结果所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。