NOIP2016提高组day2 天天爱跑步

Description

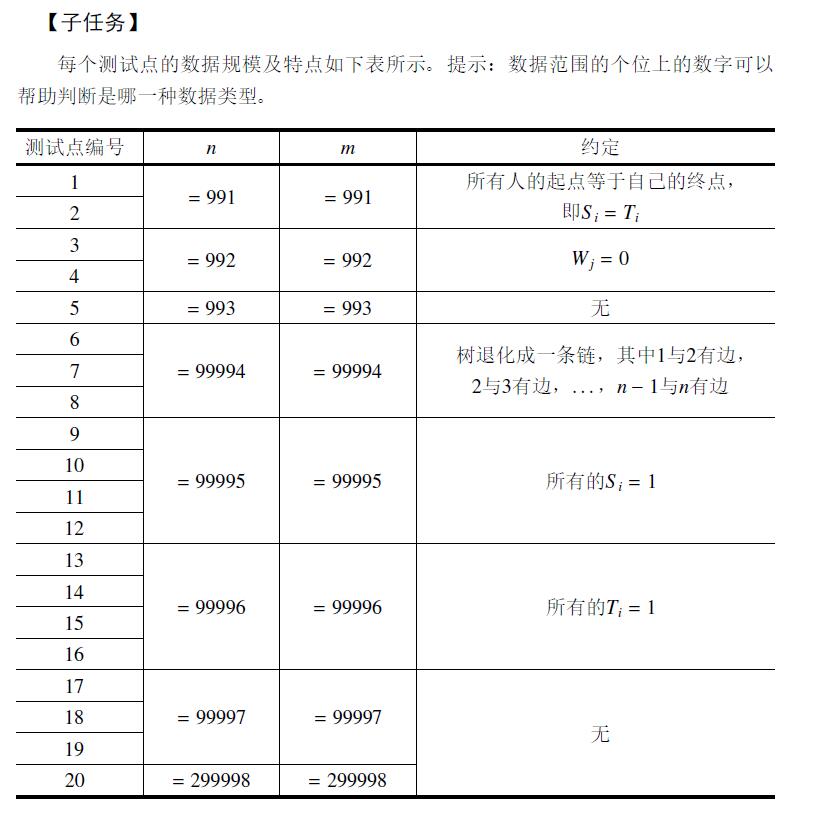
Data Constraint

Solution

我们可以设一个询问[S,T]的lca为X，路径的长度为a[i]，那么一个询问可以拆成[S,T]和[X,T]拆成两部分。

对于一个在[S,T]路径上的点j，假如有贡献一定满足d[s]-d[j]=w[j],移一下项就变成d[s]=w[j]+d[j]，这样右边就变成只与j有关，左边只与s有关。

对于一个在[X,T]路径上的点j，假如有贡献一定满足d[t]-d[j]=a[i]-w[j],移一下项就变成d[t]-a[i]=d[j]-w[j]，这样右边就变成只与j有关，左边只与t,i有关。

于是我们先将询问都挂在树上，对树做一个深度优先遍历，每次做到一个点，先将这个点上的询问d[t]-a[i]或d[s]加入权值线段树内，做完这个点的子树后在查询答案就好了，要将这个点的答案用线段树合并到他的父亲。

**注意：1、一个询问挂在s或t上后，要在他们的lcaX上有删除操作
2、d[i]表示一个点的深度**

Code

#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=6*1e5+5,maxn1=3*1e5+5;
int first[maxn],last[maxn],next[maxn],f[maxn1][20],deep[maxn],first1[maxn],last1[maxn],next1[maxn],w[maxn];
int a[maxn],first2[maxn],last2[maxn],next2[maxn],g[2][maxn*10],f1[maxn*10][2],ans[maxn1],first3[maxn],last3[maxn],next3[maxn];
int n,m,i,t,j,k,l,x,y,z,num,ln,r,mid,num1,num2,num3,d[maxn1],v[maxn1],p;
bool bz[maxn],bz1;
void lian(int x,int y){
last[++num]=y;next[num]=first[x];first[x]=num;
}
void lian1(int x,int y){
last1[++num1]=y;next1[num1]=first1[x];first1[x]=num1;
}
void lian2(int x,int y){
last2[++num2]=y;next2[num2]=first2[x];first2[x]=num2;
}
void lian3(int x,int y){
last3[++num3]=y;next3[num3]=first3[x];first3[x]=num3;
}
void bfs(){
deep[1]=1;
v[1]=j=1;i=0;
while (i<j){
x=v[++i];bz[x]=true;
for (t=first[x];t;t=next[t]){
if (bz[last[t]])continue;
bz[last[t]]=true;
v[++j]=last[t];deep[last[t]]=deep[x]+1;f[last[t]][0]=x;
}
}
v[0]=j;
}
int lca(int x,int y){
int j,k=0;
if (deep[x]<deep[y]) swap(x,y),k=1;
for (j=ln;j>=0;j--)
if (deep[f[x][j]]>=deep[y]) x=f[x][j];
if (x==y)return x;
for (j=ln;j>=0;j--)
if (f[x][j]!=f[y][j]) x=f[x][j],y=f[y][j];
if (k) p=y;
else p=x;
return f[x][0];
}
void insert(int l,int r,int &v,int x,int y,int z){
if(!v) v=++num;
int mid=(l+r)/2;
if (l==r){
g[z][v]+=y;return;
}
if (mid>=x) insert(l,mid,f1[v][0],x,y,z);
else insert(mid+1,r,f1[v][1],x,y,z);
}
int find(int l,int r,int v,int x,int z){
if (!v) return 0;
int mid=(l+r)/2;
if (l==r) return g[z][v];
if (mid>=x) return find(l,mid,f1[v][0],x,z);
else return find(mid+1,r,f1[v][1],x,z);
}
void make(int l,int r,int &v,int v1){
if (!v1) return;
if (!v){
v=++num;f1[v][0]=f1[v1][0];f1[v][1]=f1[v1][1];
g[0][v]+=g[0][v1];g[1][v]+=g[1][v1];
return;
}
if (l==r){
g[0][v]+=g[0][v1];g[1][v]+=g[1][v1];return;
}
int mid=(l+r)/2;
make(l,mid,f1[v][0],f1[v1][0]);make(mid+1,r,f1[v][1],f1[v1][1]);
}
int main(){
freopen("running.in","r",stdin);freopen("running.out","w",stdout);
scanf("%d%d",&n,&m);
for (i=1;i<n;i++)
scanf("%d%d",&x,&y),lian(x,y),lian(y,x);
bfs();
for (i=1;i<=n;i++)
scanf("%d",&w[i]);
ln=log(n)/log(2);
for (j=1;j<=ln;j++)
for (i=1;i<=n;i++)
f[i][j]=f[f[i][j-1]][j-1];
num=0;
for (i=1;i<=m;i++){
scanf("%d%d",&x,&y);
t=lca(x,y);
if (x==y && !w[x]) ans[x]++;
if (x!=t){
a[x]++;
if (y==t) lian2(t,deep[x]);
else lian2(p,deep[x]);
}
if (y!=t){
k=deep[x]+deep[y]-2*deep[t];
lian1(y,deep[y]-k+maxn1);
lian3(t,deep[y]-k+maxn1);
}
}
num=0;
for (i=v[0];i>0;i--){
x=v[i];
if (a[x]) insert(1,maxn,d[x],deep[x],a[x],0);
for (t=first1[x];t;t=next1[t])
insert(1,maxn,d[x],last1[t],1,1);
ans[x]+=find(1,maxn,d[x],deep[x]+w[x],0);
ans[x]+=find(1,maxn,d[x],deep[x]-w[x]+maxn1,1);
for (t=first2[x];t;t=next2[t])
insert(1,maxn,d[x],last2[t],-1,0);
for (t=first3[x];t;t=next3[t])
insert(1,maxn,d[x],last3[t],-1,1);
make(1,maxn,d[f[x][0]],d[x]);
}
for (i=1;i<=n;i++)
printf("%d ",ans[i]);
return 0;
}

最后

以上就是留胡子便当为你收集整理的NOIP2016提高组day2 天天爱跑步的全部内容，希望文章能够帮你解决NOIP2016提高组day2 天天爱跑步所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。