铁水调度的路径规划—最短路径的两种算法
- 背景介绍
- Dijkstra算法
- Floyd算法
背景介绍
小编接到一个铁水运输的调度任务,该任务暂定分为三部分,第一期定为较简单的路径规划(指定机车头的起始、终点位置),确定最优路径。
实际任务的路径规划,了解业务逻辑后发觉,其实往往现实生活中与算法有一定区别:比如客户有时候最关心的问题不是最短、最优,而是你在一个合理的范围内,安全、稳定是系统的首要前提,但是也不逼逼了,直接上今天我学到的这两个算法。
Dijkstra算法
一、最短路径
显而易见,在非网图中,最短路径是指两顶点经历的边数最少的路径;而在网图中,最短路径是指两顶点间经历的权值之后最短的路径。
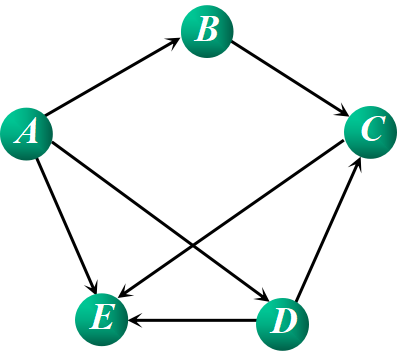
AE:1 ADE:2 ADCE:3 ABCE:3
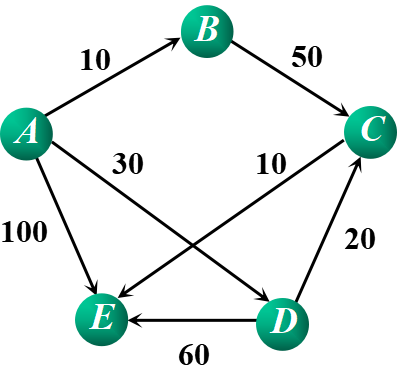
AE:100 ADE:90 ADCE:60 ABCE:70
然后该算法的思想很简单,属于贪心算法,具体如下:
1、指定一个节点,例如我们要计算 ‘A’ 到其他节点的最短路径
引入两个集合(S、U),S集合包含已求出的最短路径的点(以及相应的最短长度),U集合包含未求出最短路径的点(以及A到该点的路径,注意 如上图所示,A->C由于没有直接相连 初始时为∞)
2、初始化两个集合,S集合初始时 只有当前要计算的节点,A->A = 0,
U集合初始时为 A->B = 4, A->C = ∞, A->D = 2, A->E = ∞,敲黑板!!!接下来要进行核心两步骤了
3、从U集合中找出路径最短的点,加入S集合,例如 A->D = 2
4、更新U集合路径,if ( ‘D 到 B,C,E 的距离’ + ‘AD 距离’ < ‘A 到 B,C,E 的距离’ ) 则更新U
循环执行 4、5 两步骤,直至遍历结束,得到A 到其他节点的最短路径
其实吧(参考https://www.jianshu.com/p/ff6db00ad866)
就是如果确定了A-D的的距离最短为2,则下一步的更新条件为:“D到B、C、E的距离”+“AD最短距离”<A到B、C、E的距离 则更新
Floyd算法
今天我们讨论的是floyd算法,它用于解决多源最短路径问题,算法时间复杂度是O(n3).floyd算法为什么经典,因为它只有5行(或者4行)!!!
是的,没有特意的写成一行的代码.

这个算法短的离谱,以致于我们通常直接将它背了下来当模板使用,而不像学dijkstra那时候一步步理解它是如何贪心的。至于为什么这四步就能找到任意两点的最短路径呢?精妙之处,就是在K放在最外层。
我们可以利用归纳法,证明得到一个很致命的结论:
假设i和j之间的最短路径上的结点集里(不包含i,j),编号最大的一个是x.那么在外循环k=x时,d[i][j]肯定得到了最小值。
证明过程参考博客https://blog.csdn.net/xianpingping/article/details/79947091
最后
以上就是震动大门最近收集整理的关于铁水调度的路径规划—最短路径的两种算法背景介绍Dijkstra算法Floyd算法的全部内容,更多相关铁水调度内容请搜索靠谱客的其他文章。








发表评论 取消回复