日萌社

人工智能AI：Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战（不定时更新）

1.最常出现的对置信区间的错误理解：
	在95%置信区间内，有95%的概率包括真实参数  （错误！！）
	在95%置信区下构建的模型，意味着模型参数对于试图近似的函数有95%的概率是真实值的估计值（错误！！）
2.正确解释应为：
	95%置信区间，意味着如果你用同样的步骤，去选样本，计算置信区间，那么100次这样的独立过程，有95%的概率你计算出来的区间会包含真实参数值，
	即大概会有95个置信区间会包含真值。而对于某一次计算得到的某一个置信区间，其包含真值的概率，我们无法讨论。
3.我们平常使用的频率学派（frequentist）95% 置信区间的意思并不是真值在这个区间内的概率是 95%。真值要么在，要么不在。
  由于在频率学派当中，真值是一个常数，而非随机变量（后者是贝叶斯学派） ，所以我们不对真值做概率描述。
  对于这个问题来说，理解的关键是我们是对这个构造置信区间的方法做概率描述，而非真值，也非我们算得的这个区间本身。
  换言之，我们可以说，如果我们重复取样，每次取样后都用这个方法构造置信区间，有 95% 的置信区间会包含真值。
  然而（在频率学派当中）我们无法讨论其中某一个置信区间包含真值的概率。
4.假设现在是95%的置信水平（ 95%也被称为置信水平，是统计中的一个习惯，可以根据应用进行调整），每个从总体中抽出的样本都可以求出一个95%的置信区间，
  且不同样本求出的置信区间是不同的，但随着抽出的样本次数的增加，例如抽100次，得到100个样本，每个样本都对应一个置信区间，
  那么100次抽样求出的100个置信区间有95个包含真实的总体均值。
  置信区间会因样本的不同而不同（置信区间是怎么算的？是通过样本（sample）算的），而且不是所有的区间都包含真值，
  一个区间就像是一个为了捕获总体未知参数而撒出的网，不是所有撒网的地点都能捕获我们想要的总体的参数。
5.置信区间，就是一种区间估计。

M = 1000;          %采样点数
N = 1000;          %采样组数
mu = 3.5;          
delta2 = 35/12;    %掷骰子问题理论均值及方差
c = 1.96;          %置信度95%所对应的critical value，由于总体的方差已知，这里采用z-score计算critical value
T = 100;           %重复实验次数
rate = zeros(T,1); %保存每次实验真实值落入置信区间中比例
for t = 1:T
    cnt = 0;           %统计真实值落入置信区间中的次数
    for i = 1:N
        S = randi(6,M,1);   %采样点集合
        S_mean = mean(S);   %使用样本点估计出来的均值
        CI_upper = S_mean + c*sqrt(delta2/M);          %置信区间上界
        CI_lower = S_mean - c*sqrt(delta2/M);          %置信区间下届
        %判断理论均值是否落在置信区间内
        if(CI_lower < mu & mu < CI_upper)
            cnt = cnt + 1;
        end
    end
    rate(t) = cnt / N;
end
%画图
% figure(1)
% plot(rate)
% axis([1 100 0 1])
% xlabel('实验次数')
% ylabel('真实值落入置信区间中比例')

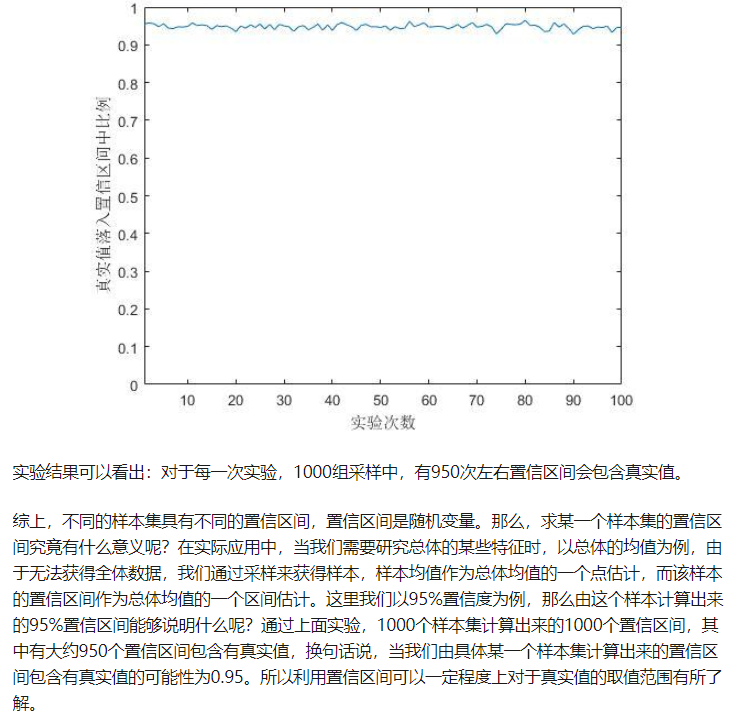
最后

以上就是过时机器猫为你收集整理的95%置信区间日萌社的全部内容，希望文章能够帮你解决95%置信区间日萌社所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。