需要源码请点赞关注收藏后评论区留言留下QQ~~~

一、带基线的REINFORCE

REINFORCE的优势在于只需要很小的更新步长就能收敛到局部最优，并保证了每次更新都是有利的，但是假设每个动作的奖赏均为正，则每个动作出现的概率将不断提高，这一现象会严重降低学习速率，并增大梯度方差

根据这一思想，我们构建一个仅与状态有关的基线函数，保证能够在不改变策略梯度的同时，降低其方差，带基线的REINFORCE算法是REINFORCE算法的改进版，原则上，与动作无关的函数都可以作为基线，但是为了对所有动作值都比较大的状态，需要设置一个较大的基线来区分最优动作和次优动作：对所有动作值都比较小的状态，则需要设置一个比较小的基线。由此用近似状态值函数代表基线，当回报超过基线值时，该动作的概率将提高，反之降低

二、结果与分析

1：实验环境设置

带基线的REINFORCE算法其网络结构，参数设置以及实验环境与REINFORCE一样，在算法中，近似状态值函数参数W的学习率为0.001，REINFORCE和带基线的REINFORCE效果对比如下图

在短走廊环境下，带基线的REINFORCE收敛的更快，并且更为稳定，

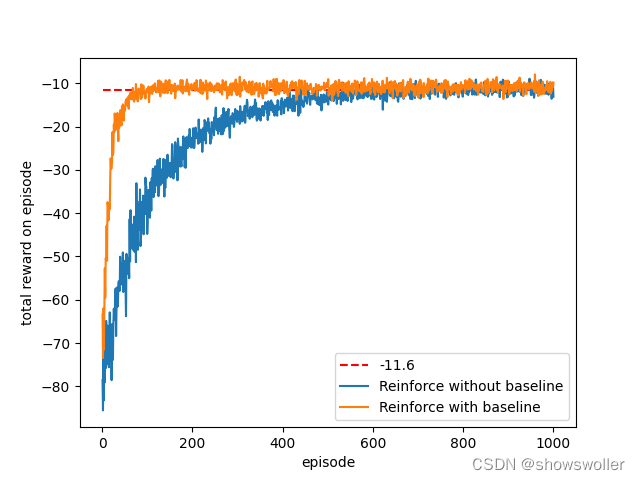
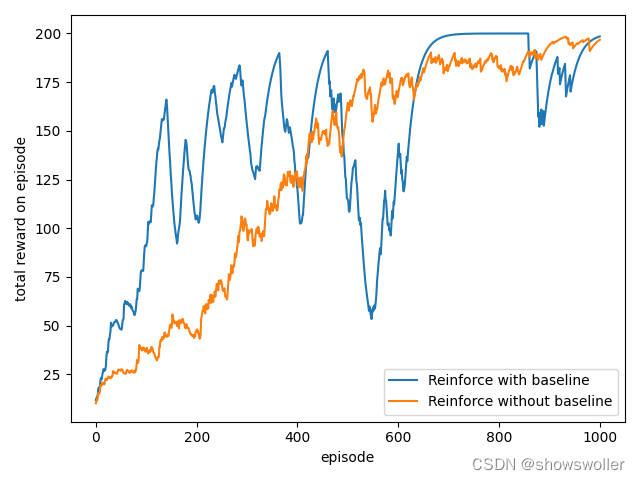
在CartPole环境下，两个算法的波动都比较大，带基线的更为明显，这是因为CartPole环境更为复杂。 

 三、代码

部分代码如下

import torch.nn as nn
import torch.nn.functional as F
import gym
import torch
from torch.distributions import Categorical
import torch.optim as optim
from copy import deepcopy
import numpy as np
import argparse
import matplotlib.pyplot as plt
from _DUPLICATE_LIB_OK"]="True"

render = False
class Policy(nn.Module):
    def __init__(self,n_states, n_hidden, n_output):
        super(Policy, self).__init__()
        self.linear1 = nn.Linear(n_states, n_hidden)
        self.linear2 = nn.Linear(n_hidden, n_output)

 #这是policy的参数
        self.reward = []
        self.log_act_probs = []
        self.Gt = []
        self.sigma = []
#这是state_action_func的参数
        # self.Reward = []
        # self.s_value = []

    def forward(self, x):
        x = F.relu(self.linear1(x))
        output = F.softmax(self.linear2(x), dim= 1)
        # self.act_probs.append(action_probs)
        return output
env = gym.make('CartPole-v0')
n_states = env.observation_space.shape[0]
n_actions = env.action_space.n
policy = Policy(n_states, 128, n_actions)
s_value_func = Policy(n_states, 128, 1)
alpha_theta = 1e-3
optimizer_theta = optim.Adam(policy.parameters(), lr=alpha_theta)
gamma = 0.99
seed = 1
e)
    plt.ylabel('Run Time')
    plt.plot(epi, run_time)
    plt.show()
if __name__ == '__main__':
    running_reward = 10
    i_episodes = []
    for i_episode in range(1, 10000):
        state, ep_reward = env.reset(), 0
        if render: env.render()
        policy_loss = []
        s_value = []
        state_sequence = []
        log_act_prob = []
        for t in range(10000):
            state = torch.from_numpy(state).unsqueeze(0).float()  # 在第0维增加一个维度，将数据组织成[N , .....] 形式
            state_sequence.append(deepcopy(state))
            action_probs = policy(state)
            m = Categorical(action_probs)
            action = m.sample()
            m_log_prob = m.log_prob(action)
            log_act_prob.append(m_log_prob)
            # policy.log_act_probs.append(m_log_prob)
            action = action.item()
            next_state, re, done, _ = env.step(action)
            if render: env.render()
            policy.reward.append(re)
            ep_reward += re
            if done:
                break
            state = next_state
        running_reward = 0.05 * ep_reward + (1 - 0.05) * running_reward
        i_episodes.append(i_episode)
        if i_episode % 10 == 0:
            print('Episode {}tLast length: {:2f}tAverage length: {:.2f}'.format(
                i_episode, ep_reward, running_reward))
        live_time.append(running_reward)
        R = 0
        Gt = []

        # get Gt value
        for r in policy.reward[::-1]:
            R = r + gamma * R
            Gt.insert(0, R)
        # update step by step
        for i in range(len(Gt)):
            G = Gt[i]
            V = s_value_func(state_sequence[i])
            delta = G - V

            # update value network
            alpha_w = 1e-3  # 初始化

            optimizer_w = optim.Adam(s_value_func.parameters(), lr=alpha_w)
            optimizer_w.zero_grad()
            policy_loss_w = -delta
            policy_loss_w.backward(retain_graph=True)
            clip_grad_norm_(policy_loss_w, 0.1)
            optimizer_w.step()

            # update policy network
            optimizer_theta.zero_grad()
            policy_loss_theta = - log_act_prob[i] * delta
            policy_loss_theta.backward(retain_graph=True)
            clip_grad_norm_(policy_loss_theta, 0.1)
            optimizer_theta.step()
        del policy.log_act_probs[:]
        del policy.reward[:]
        if (i_episode % 1000 == 0):
            plot(i_episodes, live_time)
    np.save(f"withB", live_time)
    policy.plot(live_time)

创作不易 觉得有帮助请点赞关注收藏~~~

最后

以上就是神勇豌豆为你收集整理的【PyTorch深度强化学习】带基线的蒙特卡洛策略梯度法（REINFOECE）在短走廊和CartPole环境下的实战（超详细 附源码）一、带基线的REINFORCE二、结果与分析 三、代码的全部内容，希望文章能够帮你解决【PyTorch深度强化学习】带基线的蒙特卡洛策略梯度法（REINFOECE）在短走廊和CartPole环境下的实战（超详细 附源码）一、带基线的REINFORCE二、结果与分析 三、代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。