基于实数编码的遗传算法搜寻多元函数最值

遗传算法介绍

遗传算法于20世纪70年代由美国的John holland提出，是一种通过模仿达尔文生物进化理论和遗传机制以寻求问题最优解的启发式算法。算法的运作主要依赖于三大算子：选择、交叉、变异，其算法流程如图1所示：

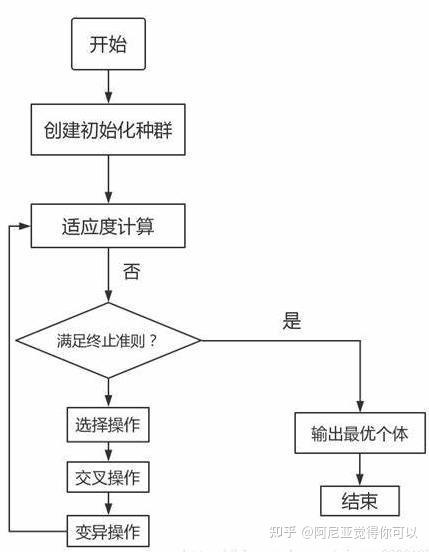
图1.遗传算法流程图

适应度函数

遗传算法中使用适应度这一概念来评定一个个体在种群中的生存能力。一个种群中个体的适应度通过对表现型结合目标函数求解所得的值的一定的变换得到，这种变换可以是幂函数变换、指数函数变换等。

选择算子

为体现自然进化理论中的优胜劣汰，遗传算法中采用选择算子来挑选种群中的优势个体并淘汰劣势个体。对种群中的个体的选择是基于适应度做出的，常用的由下列几种选择机制

轮盘赌：根据个体的适应度，计算个体存活下来的概率，再按照概率随机在种群中选择存活下来的个体，个体存活率计算公式如下： Pi=fi/(∑1nfj)，其中：Pi为个体存活率，fi为个体适应度，n为种群个体总数

截断选择：按照个体适应度从大到小将种群中所有个体重新排列，选取排列中前n％个个体进入下一代。这是一种非常简单明了的选择方式，能够都大规模种群进行快速选择。

锦标赛选择：在种群中一次抽取s个个体，取这s个个体中适应度最大的个体进入到下一代中，如此操作知道种群中所有个体完成选择。通过锦标赛选择，可以通过调节单次抽出个数s的值来达到调节选择压力的目的。s越大则劣势个体被淘汰的几率越大，但是会导致子代个体不足的情况，反之亦然。

精英选择：直接挑选出父代适应度最高的前几个个体进入子代之中。这种方法具有较好的记忆性，能够比较好的将上一代的优良个体保留下来，但是这种方法缺乏随机性，很可能会导致局部最优的情况发生。

交叉算子

交叉模拟了生物种群中交配这一行为，父代之间染色体交换某些基因片段形成新的子代染色体。值得注意的是交叉并不是必须执行的，往往会设置一个交叉概率，依据交叉概率确定交叉时才进行交叉操作（种群中两个个体看不上对方，你非让人家交配是不行的，毕竟强扭的瓜不甜~~）。浮点数编码的遗传算法往往有以下几种交叉操作：

离散交叉：直接交换两父代染色体中某些相对应的片段。如有四个基因的两父代：parent_1为： A1B1C1D1 ，parent_2为： A2B2C2D2 ，经过交叉后（彼此交换2、3号基因）生成两子代：child_1为 A1B2C2D1 ,child_2为 A2B1C1D2 。

比例交叉：两父代按一定的比例生成两子

child1=α∗parent1+(1−α)∗parent2

child2=(1−α)∗parent1+α∗parent2，α∈(0,1)

启发式交叉：在两个父代中生存能力较强的个体的基础上生成子代。

child=parent优+r∗(parent优−parent劣)，其中r为子代与优势父代之间的差距，r∈(0,1)

变异算子

只需在个体染色体某一处或某几处特定的基因片段在约束许可的范围内产生变异既可,同交叉相同，变异也存在变异概率。

程序介绍

问题描述

寻找如下多元函数最大值： f=cos(x1)+x2∗x3 ，其中有约束条件： x1+x2+x3≤20 。

适应度选择

该问题中直接选择多元函数值 f 作为个体适应度，适应度函数如下：

#定义适应度deffitness(group):fitness=[]forindivitualingroup:fitness_indvitial=np.cos(indivitual[0])+(indivitual[1])*(indivitual[2])fitness.append(fitness_indvitial)returnfitness

选择算子设置

程序中的选择算子的设置结合了精英选择和轮盘赌两种选择方法。首先将种群中生存能力最高的几个个体直接选择出来进入子代，这样保证了优势个体不会被筛选掉，提高算法效率。同样为了避免陷入局部最优解的情况，采用轮盘赌的方法对父代剩下的个体进行选择。经过程序的一番调试之后，将每一轮的存活率设定为99％。选择算子程序如下：

#定义选择算子
def choice(group,fitness):
    choice_group=[]
    for reduce_num in range(0,3): #选择出最优的三个个体进入下一代
        choice_group.append(group[fitness.index(max(fitness))])
        group[0],group[fitness.index(max(fitness))]=group[fitness.index(max(fitness))],group[0]
        group.remove(max(group))
        fitness[0],fitness[fitness.index(max(fitness))]=fitness[fitness.index(max(fitness))],fitness[0]
        fitness.remove(max(fitness))
    fitness_rate = np.array(fitness) / sum(fitness)
    fitness_roundel = [0]
    for n in range(0, len(fitness_rate)):  # 生成轮盘
        fitness_roundel.append(sum(fitness_rate[:n + 1]))
    for j in range(0,int(survive_rate*len(fitness_roundel))):
        index = random.random()
        for i in range(0, len(fitness_roundel) - 1):
            if index >= fitness_roundel[i] and index < fitness_roundel[i + 1]:
                choice_group.append(group[i])
    return choice_group

交叉算子设置

该程序采用比例交叉的方法执行交叉操作，比例交叉中比例因子 α 设置为0.4。为了保证产生优势个体，交叉后的会在父代和子代中在次进行选择，选出四个中生存能力最强的两个（写这段代码是我的心里其实是有点震惊的。结合前不久看的1984这本书，为了生存，或者说为了得出最优个体，父母和子女之间竟然可以互相残杀，彼此举报）。考虑到约束条件的存在，为避免产生的子代突破约束，会对子代进行一次判定，合格后方可进入家庭内的选优，若突破了约束条件，则将该个体设置为[0,0,0],视其为一个死胎，程序如下：

#交叉算子
def cross(group,parent_1,parent_2):
    child_1=0.4*np.array(parent_1)+0.6*np.array(parent_2) #产生两个子代
    child_2=0.6*np.array(parent_1)+0.4*np.array(parent_2)
    if sum(child_1)>20: #判定是否为死胎
        child_1=[0,0,0]
    if sum(child_2)>20:
        child_2=[0,0,0]
    family=[child_1,child_2,parent_1,parent_2]  #残酷的家庭竞争
    for i in range(0,len(family)):
        family[i]=list(family[i])
    family_fitness=fitness(family)
    survive_1=family[family_fitness.index(max(family_fitness))]
    family.remove(survive_1)
    family_fitness.remove(max(family_fitness))
    survive_2=family[family_fitness.index(max(family_fitness))]
    group[group.index(parent_1)]=survive_1
    group[group.index(parent_2)]=survive_2

变异算子设置

变异算子的设置则是简单的第二号位的基因在许可的范围内产生变异。变异前后个体同样会进行判断以选择最优个体，程序如下：

#变异算子
def variation(indivitual):
    temp_indivitual=indivitual
    indivitual[1]=random.uniform(0,20-indivitual[0]-indivitual[2])
    variation_pair=[temp_indivitual,indivitual]
    variation_fitness=fitness(variation_pair)
    return variation_pair[variation_fitness.index(max(variation_fitness))]

完整程序展示及计算结果

完整程序

import random
import numpy as np
import matplotlib.pyplot as plt
#计算适应度
def fitness(group):
    fitness=[]
    for indivitual in group:
        fitness_indvitial=np.cos(indivitual[0])+(indivitual[1])*(indivitual[2])
        fitness.append(fitness_indvitial)
    return fitness

#定义选择算子
def choice(group,fitness):
    choice_group=[]
    for reduce_num in range(0,3):
        choice_group.append(group[fitness.index(max(fitness))])
        group[0],group[fitness.index(max(fitness))]=group[fitness.index(max(fitness))],group[0]
        group.remove(max(group))
        fitness[0],fitness[fitness.index(max(fitness))]=fitness[fitness.index(max(fitness))],fitness[0]
        fitness.remove(max(fitness))
    fitness_rate = np.array(fitness) / sum(fitness)
    fitness_roundel = [0]
    for n in range(0, len(fitness_rate)):  # 生成轮盘
        fitness_roundel.append(sum(fitness_rate[:n + 1]))
    for j in range(0,int(survive_rate*len(fitness_roundel))):
        index = random.random()
        for i in range(0, len(fitness_roundel) - 1):
            if index >= fitness_roundel[i] and index < fitness_roundel[i + 1]:
                choice_group.append(group[i])
    return choice_group

#变异算子
def variation(indivitual):
    temp_indivitual=indivitual
    indivitual[1]=random.uniform(0,20-indivitual[0]-indivitual[2])
    variation_pair=[temp_indivitual,indivitual]
    variation_fitness=fitness(variation_pair)
    return variation_pair[variation_fitness.index(max(variation_fitness))]

#交叉算子
def cross(group,parent_1,parent_2):
    child_1=0.4*np.array(parent_1)+0.6*np.array(parent_2)
    child_2=0.6*np.array(parent_1)+0.4*np.array(parent_2)
    if sum(child_1)>20:
        child_1=[0,0,0]
    if sum(child_2)>20:
        child_2=[0,0,0]
    family=[child_1,child_2,parent_1,parent_2]
    for i in range(0,len(family)):
        family[i]=list(family[i])
    family_fitness=fitness(family)
    survive_1=family[family_fitness.index(max(family_fitness))]
    family.remove(survive_1)
    family_fitness.remove(max(family_fitness))
    survive_2=family[family_fitness.index(max(family_fitness))]
    group[group.index(parent_1)]=survive_1
    group[group.index(parent_2)]=survive_2
 ##################################################################################

#获取初始种群
group_num=0
group=[]
while group_num<300:
    x_1 = random.uniform(0, 20)
    x_2 = random.uniform(0, 20 - x_1)
    x_3 = random.uniform(0, 20 - x_2 - x_1)
    indivitual=[x_1,x_2,x_3]
    group.append(indivitual)
    group_num=group_num+1
print("初始种群为：",group)
m=fitness(group)
print(m)
#开始进化
P_c=0.90  #交叉概率
P_v=0.05  #变异概率
survive_rate=0.99  #种群存活概率
fitness_variation_min=[]  #用于纪录适应度变化
fitness_variation_max=[]
for generation in range(0,500):
   #计算每一代适应度
    print("正在计算第",generation,"代")
    fitness_generation=fitness(group)  #计算每代群体适应度
    fitness_variation_min.append(min(fitness_generation))
    fitness_variation_max.append(max(fitness_generation))
    #开始选择
    new_group=choice(group,fitness_generation)
    #index_max=fitness_generation.index(max(fitness_generation))
    #判断是否进行交叉操作，判定结果为真时进行交叉操作
    rate_cross=random.random()
    if rate_cross<=P_c:
        father_index=random.randint(0,len(new_group)-1)
        mother_index=random.randint(0,len(new_group)-1)
        while father_index in [0,1,2] or mother_index in [0,1,2]:
            father_index = random.randint(0, len(new_group) - 1)
            mother_index = random.randint(0, len(new_group) - 1)
        father=new_group[father_index]
        mother=new_group[mother_index]
        cross(new_group,father,mother)
    rate_variation=random.random()
    #判断是否进行变异操作，判定结果为真时进行变异操作
    if rate_variation<=P_v:
        indivitual_index=random.randint(0,len(new_group))
        while indivitual_index in [0,1,2]:
            indivitual_index = random.randint(0, len(new_group))
        new_group[indivitual_index]=variation(new_group[indivitual_index])
    group=new_group
print(new_group)
print("最优个体为：",new_group[fitness_generation.index(max(fitness_generation))],'其适应度为：',max(fitness_generation))
#plt.plot(fitness_variation_min,'red')
plt.plot(fitness_variation_max)
plt.show()

计算结果

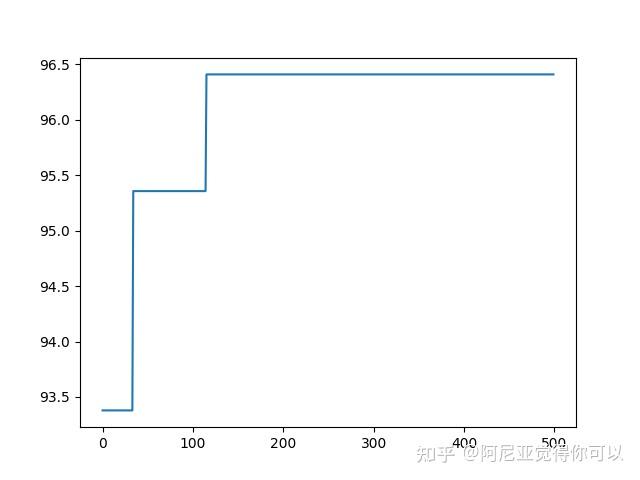
图2.适应度变化曲线

最优个体

最优个体为：[0.42334915510184645, 9.826321901393053, 9.637997536227205]，适应度（函数值）为：95.01500046525271