内容基于《人工神经网络理论,设计及应用》的学习,对重点进行了摘抄总结,网上许多博客的内容也基于此。
玻尔兹曼机是一种随机神经网络,借鉴了模拟退火思想。
随机神经网络与其他神经网络相比有两个主要区别 :
① 在学习(训练)阶段 , 随机网络不像其他网络那样基于某种确定性算法调整权值,而是按某种概率分布进行修改;(通俗解释,Hopfield网络的权值用某种方法一步确定,而玻尔兹曼机像BP网络一样,每训练一次,权值改变一次。)
② 在运行(预测)阶段,随机网络不是按某种确定性的网络方程进行状态演变,而是按某种概率分布决定其状态的转移。神经元的净输入不能决定其状态取1还是取0,但能决定其状态取1还是取0的概率。这就是随机神经网络算法的基本概念。(Hopfield网络后一状态的值由前一状态决定,玻尔兹曼机后一状态的值受到前一状态影响。)
网络有两种类型,如下图,可以先不去理解,有个大致印象就行,后面有解释,其中隐节点个数可以为0。不明白为何有些线不是双向的,按分析,所有权值都对称,应该都是双向箭头?
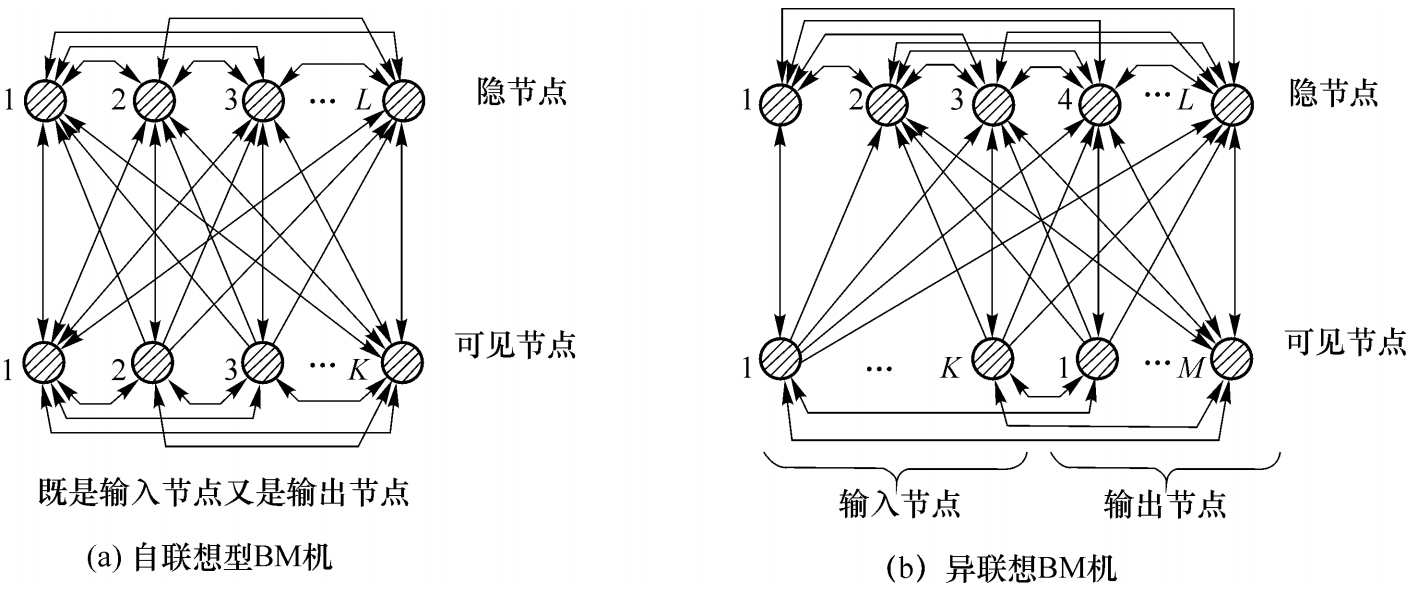
预测阶段
设 BM 机中单个神经元的净输入为 :
![]()
与DHNN不同的是,净输入并不能通过符号转移函数直接获得确定的输出状态,实际的输出状态将按照某种概率发生,输出某种状态的转移概率:
![]()
上式表示的是神经元j输出状态为1的概率,状态为0的概率为:
$$P_{j}(0)=1-P_{j}(1)$$
构建能量函数,证明按上述步骤,能量会减小。
BM机采用的与DHNN网络相同的能量函数描述网络状态,如下图所示:
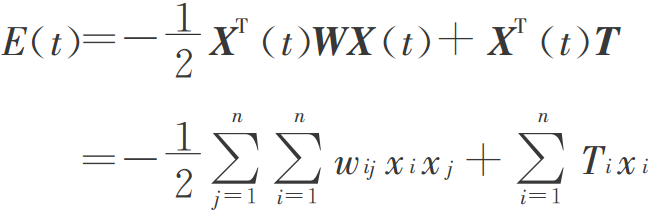
设BM机按异步方式工作,每次第j个神经元改变状态,根据能量变化公式:
![]()
对上式进行讨论:
(1) 当时,有
,即神经元有较大的概率取
。若原来
,则
,从而
;若原来
,则
,从而
。
(2) 当时,有
,即神经元有较大的概率取
。若原来
,则
,从而
;若原来
,则
,从而
。
以上对各种可能的情况讨论中可以看出,对于BM机,随着网络状态的演变,从概率意义上网络的能量总是朝着减小的方向变化。这就意味着尽管网络能量的总趋势是朝着减小的方向演进,但不排除在有些神经元状态可能会按照小概率取值,从而使网络能量暂时增加。正是因为有了这种可能性,BM机才具有了从局部极小的低谷中跳出的“爬山”能力,这一点是BM机与DHNN网能量变化的根本区别。
采用上述模拟退火算法进行最优解的搜索,开始时温度设置很高,此时神经元状态为1或0概率几乎相等,因此网络能量可以达到任意可能的状态,包括局部最小或全局最小。当温度下降,不同状态的概率发生变化,能量低的状态出现的概率大,而能量高的状态出现的概率小。当温度逐渐降至0时,每个神经元要么只能取1,要么只能取0,此时网络的状态就凝固在目标函数全局最小附近。对应的网络状态就是优化问题的最优解。
计算过程例子http://blog.sina.com.cn/s/blog_c0ea025f0102xhk0.html,该例子最后第二图描述了某个起始状态变化为某个末状态的过程,得到状态![]() 。也就是最后得到的某个固定的状态,这与训练阶段不同,训练阶段的输入输出是各个状态的概率分布,比如
。也就是最后得到的某个固定的状态,这与训练阶段不同,训练阶段的输入输出是各个状态的概率分布,比如 。
。
训练阶段
偷懒直接截图了,有些地方解释下。
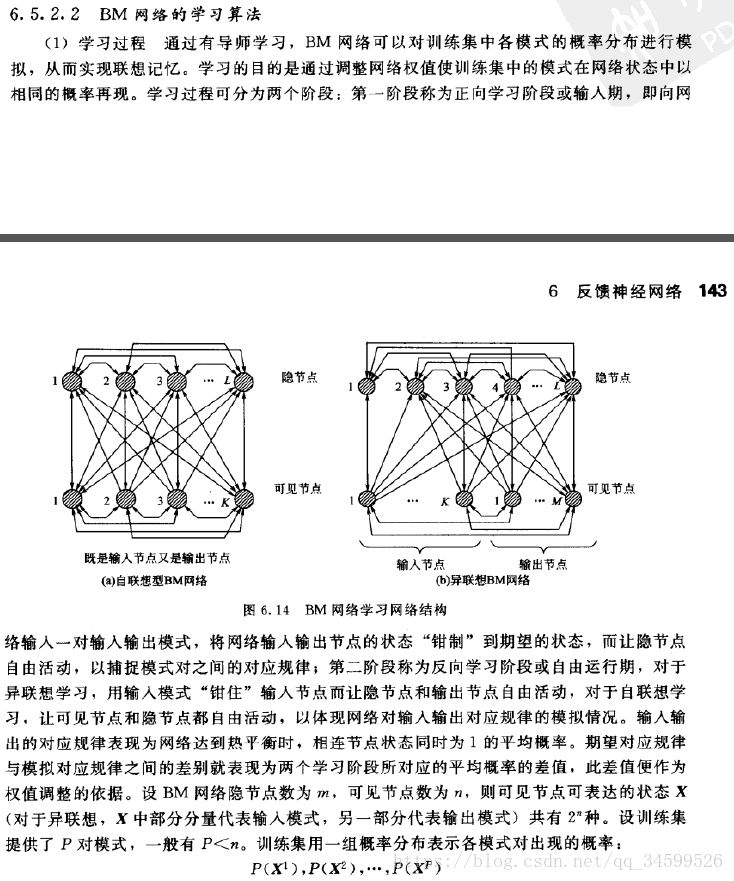


1.下面3个句子表达的同个意思,比如输入固定为 。
。
![]() ,
,

![]()
2.下面3个句子表达的同个意思。
![]()
![]()
![]()
这里有个疑问,如果像预测那样,最后结果就是个固定的状态,注意状态由节点构成,那么节点是0还是1就是个确定值,两节点同时为1就不是个概率,也是个确定的分数。因此猜想训练阶段T不降为0,这样概率才存在。
贴上一个网课的训练总结。
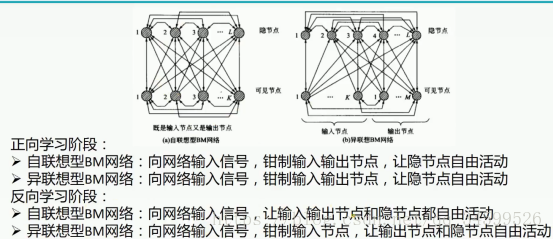
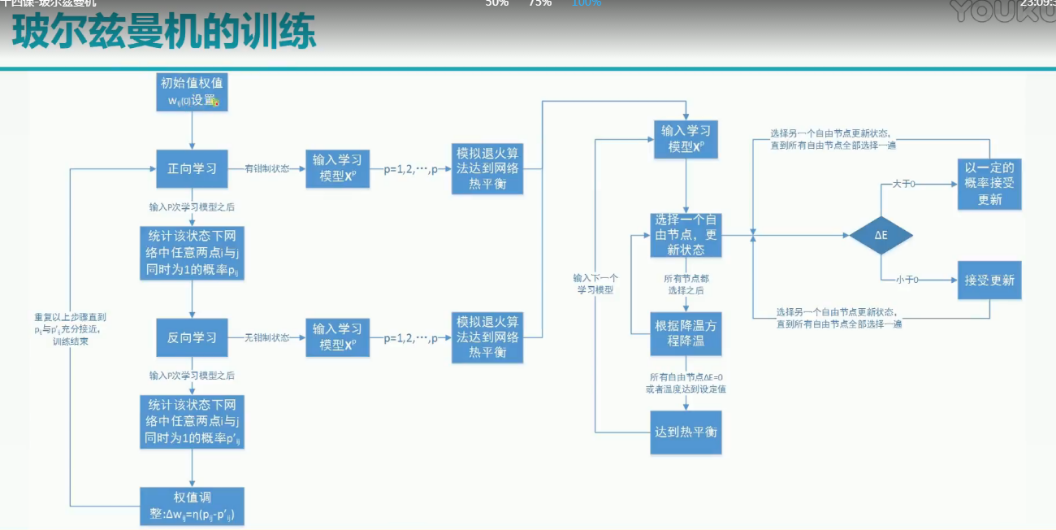
遗留问题
懒得去深入了解了。
1.网络的训练如果提供了P对模式,那么预测时是否会按照P对模式的概率产生固定状态,是否会出现其他状态?因为DHNN也会出现非人为设置的吸引子,且难以预知,称为伪吸引子。
2.训练学习的目的是对分布进行联想记忆,那么为何![]() 就能达到这个结果?以及为何权值这样调整
就能达到这个结果?以及为何权值这样调整![]() 就能使
就能使![]() ?
?
最后
以上就是稳重早晨最近收集整理的关于玻尔兹曼机(BM)的全部内容,更多相关玻尔兹曼机(BM)内容请搜索靠谱客的其他文章。








发表评论 取消回复