深度学习 --- Hopfield神经网络详解

       前面几节我们详细探讨了BP神经网络，基本上很全面深入的探讨了BP，BP属于前馈式类型，但是和BP同一时期的另外一个神经网络也很重要，那就是Hopfield神经网络，他是反馈式类型。这个网络比BP出现的还早一点，他的学习规则是基于灌输式学习，即网络的权值不是通过训练出来的，而是按照一定规则计算出来的， Hopfield神经网络就是采用了这种学习方式，其权值一旦确定就不在改变，而网络中各神经元的状态在运行过程中不断更新，网络演变到稳定时各神经元的状态便是问题之解。在这里简要解释一下为什么要学习这个神将网络，因为深度学习算法起源来源于这里还有BP，从这里开始后面会引入玻尔兹曼机、受限玻尔兹曼机、深度置信网络，径向基逼向器、卷积神经网络、递归神经网络。因此从这里一步步的深入进去是很好的开始，等到卷积你会有总体感，不会觉得太突兀。

         Hopfield神经网络分为离散型和连续型两种网络模型，分别记为DHNN（Discrete Hopfield Neural Network）和CHNN（Continues  Hopfield Neural Network）,这里主要讨论离散型网络模型，下面默认都是离散型的。

1.DHNN工作原理:

如上图是离散型网络的拓扑结构图，这是单层全反馈网络，共有n个神经元 。任一神经元的输出均通过连接权接收所有神经元输出的反馈回来的信息，其目的就在于任何一个神经元都受到所有神经元输出的控制，从而使各神经元的输出相互制约，每个神经元均设有一个阈值,目的是反映对输入的噪声的控制。DHNN网络可简记为.,他们是全连接的，上图看不清楚，看下图：

(1)网络的状态

         DHNN网络中的每个神经元都有相同的功能，其输出称为状态，用表示，所有神经元状态构成的反馈网络的状态,反馈网络的初始状态为输入表示为,一旦初始值给定后，网络就开始进行动态演变，网络中的每个神经元的状态在不断的变化，变化规律如下：

            式中，为激活函数（转移函数），通常为符号函数：

              输入为;

对于DHNN网络，一般有.

当网络的每个神经元的状态都不在改变时，此时的转态就是网络的输出转态，表示为：

(2) 网络的异步工作方式

                所谓异步是针对权值更新来说的，网络运行时每次只有一个神经元的i按照(1)式进行转态的更新，其他神经元的状态权值不变，即：

          神经元状态的调整可以按照预先设定顺序进行调整，也可以随机选定。

（3）网络的同步工作方式

                 和异步相对应，网络的同步工作方式是一种并行方式，所有神经元同时调整状态，即：

2、Hopfield神经网络的稳定性分析

    Hopfield神经网络按神经动力学的方式进行运行，工作过程为状态的演化过程，对于给定的初始状态，按照能力减小的方式演化，最终达到稳定的状态。神经动力学分为确定性神经动力学和统计性的神将动力学，前者将神经网络作为确定性行为，用非线性微分方程来描述，方程的解以概率的方式给出。

      网络从初态开始，若能经过有限次递归后，其状态不在发生变化即,则称为网络是稳定的，如果网络是稳定的，他可以从任意初态收敛到稳态，反之如果网络不稳定，但是因为每个神经元只有两个状态即0,1，因此在整体也不会呈现发散的状态，可能出现限幅的自持振荡，这种网络成为有限环网络，如果网络转态即不重复也不停止。转态变化无情多个，则为混沌现象。如下图所示：

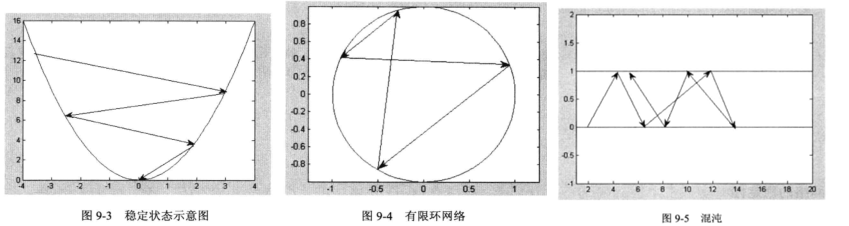
3、吸引子与能量函数         

        网络达到稳定时的状态，称为网络的吸引子。一个动力学的系统的最终行为是由他的吸引子决定的，若把需要记忆的样本信息存储于不同的吸引子中，当输入含有部分记忆信息的样本时，网络的演变过程便是从部分信息寻找全部信息，即联想回忆的过程。

        下面给出DHNN网络的吸引子的定义和定理：

         1.  若网络状态满足 ，则称为网络的吸引子

          2.对于DHNN网络，若按照异步方式调整网络的状态，且连接权矩阵为对称阵，则对于任意的初态，网络都最终收敛到一个吸引子中。

下面通过能量函数对对定理1进行证明：

定义网络的能量函数为：

                                                                     (2)

这个函数是根据动力学来的，来源我也不是很清楚，我们只需接受即可。

令网络能量的改变量为，网络状态的改变量为，则：

                                                                                          (3)

                                                                                        (4)

将（3）、（4）两式代入（2）式得：

按照上面的异步工作方式，第t个时刻只有一个神经元调整状态，设该神经元为j，将代入上式，并考虑w为对称矩阵：

因为各自神经元不存在自反馈，所以， = 0,并将上式化简为：

                                                                                                (5)

下面我们就要针对进行讨论：

情况1.    即输入输出为异号时，根据（4）式得到，因此,代入（5）式得 到：

                                   .

         注：这里解释一下，因为，而经过sgn（net_j）后，说明,否则得不到                                         ，因为符号函数要想得到1，输入必须大于等于0，下面一样的思考。

情况2.     ，即输入输出为同号时，根据（4）式得到，因此,代入（5）式                     得 到：

                                  .

情况3.      ，所以，从而得到：

下面继续讨论收敛于常数时，是否对应于网络的稳态，当收敛与常数时，此时的，此时对应两种情况：

   情况1， 或者，这种情况下，神经元的状态不在改变，表明已经达到稳态                   了，此时对应的网络状态为吸引子状态。

   情况2，  ,这种情况下网络继续演变时，将不会在变化，如果由1变化                          为-1，此时，因此和收敛常数相矛盾。

综上所述，当网络工作方式和权值满足定理时则一定收敛到一个吸引子。

定理2：

            对于DHNN网络，若按照同步方式进行调整，且连接权矩阵w为非负定对称矩阵，对于任意初态，网络都能收敛到一个吸引子上。

总结;

           从上面可以看到，异步更新要比同步更新更好，当网络的能量始终向减小的方向演变，当能量最终稳定与一个常数时，该常数对应网络能量的极小状态，称该网络的极小状态为能量井，能量井对应网络的吸引子。

好， 到这里我们知道了什么是吸引子，下一节就详细的讲解一下吸引子，本节结束。

最后

以上就是鳗鱼机器猫为你收集整理的深度学习 --- Hopfield神经网络详解的全部内容，希望文章能够帮你解决深度学习 --- Hopfield神经网络详解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。