1. 首页
  2. 文章中心
  3. cg

一个简单光栅器的实现(五) 光栅化阶段画线算法（Bresenham算法）扫描线算法Z-Buffer消隐算法纹理插值

116 阅读 0 评论
我是靠谱客的博主 搞怪荷花，这篇文章主要介绍一个简单光栅器的实现(五) 光栅化阶段画线算法（Bresenham算法）扫描线算法Z-Buffer消隐算法纹理插值，现在分享给大家，希望可以做个参考。

在几何阶段我们通过顶点变换获得了世界坐标下的顶点最终渲染到屏幕上的位置和它们的深度值，并且在剔除掉了不在视锥体内顶点，接下来要做的就是根据顶点的位置和三角形索引渲染出模型的每一个三角形。

这个简单的光栅器会实现三种渲染模式，分别是贴图模式、顶点插值和线框模式。

对于线框模式，需要做的就是根据每一个边的端点的坐标，通过计算，找出最拟合这条直线的一系列的像素。

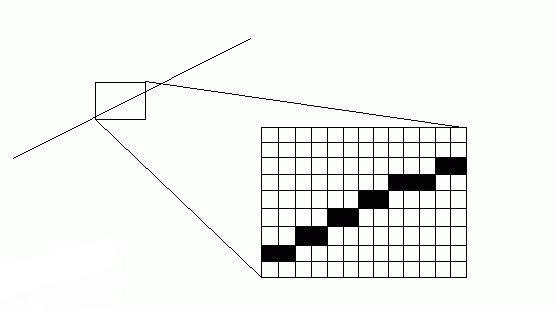
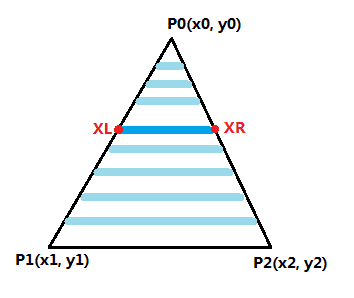
而贴图模式和顶点插值模式模式的渲染方式是将三角形切成若干条平行于x轴的直线，一般把这些直线叫做扫描线，划分好扫描线后，就可以根据扫描线左侧的起始点和右侧的终止点进行插值，计算出扫描线上每个像素点的xy坐标，uv坐标和深度值等信息。

画线算法（Bresenham算法）

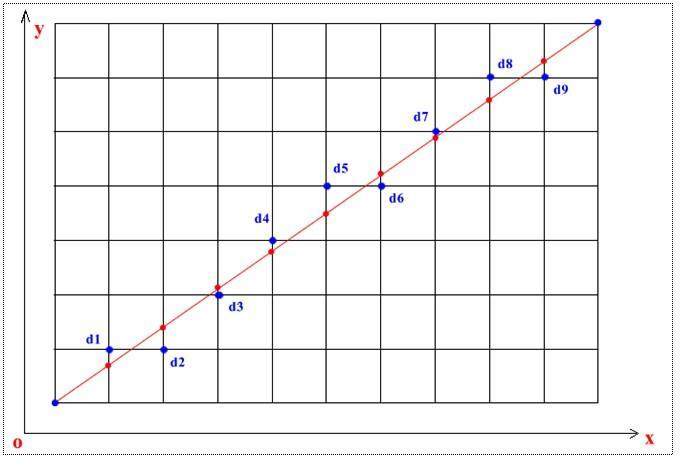
下面介绍Bresenham算法的基本思想，假设直线左下角的点为v1，右上角的点为v2

以上图为例，我们可以知道直线的斜率k小于1，即x每增加单位距离dx，y的变化量dy要比x小，在这种情况下我们以x为基准执行算法

  1. 从点v1开始，x坐标每一次迭代增加单位距离，y坐标的不变
  2. 在直线v1v2上x坐标每增加单位距离，y坐标的变化量dy是相同的，使用一个变量error记录y的累积的变化量
  3. 当y坐标累积的变化量error大于等于x的单位距离的时候，将y的累积的变化量error减去x的单位距离，同时下次迭代的时候将y坐标的值增加单位距离

上图所描述的情况直线在v1v2方向上，随着x的增加y也是增加的。如果y随x的增加而减少，那么在步骤3中修改y坐标时就应该减去单位距离

同理，当直线的斜率k大于1的时候，只需要以y轴为基准，执行上述算法即可

另外还有三种特殊的情况，即直线重合为一点、与x轴平行和与y轴平行，这三种情况处理起来就比较简单了

可以看到Bresenham算法通过采用统计误差的方式，使用步进的思想，使得每次迭代的时候只要检查一个误差项，就可以确定该列所求的像素

另外Bresenham算法避免了浮点运算，效率较高也避免了浮点数带来的误差

下面这段代码是光栅器中运用Bresenham算法的部分，在实现的时候可以将y坐标累积的变化量error和x的单位距离同时增大（v2x-v1x)倍，这样每次y的积累的变化量就是（v2y-v1y)了，x的单位距离扩大（v2x-v1x)倍后就是（v2x-v1x)了，这样可以减少很多计算

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
void Device::DrawLine(Vector2i& v1, Vector2i& v2, _UINT32 color)
{
    //两个点重合的情况
    if (v1 == v2)
    {
        DrawPixel(v1._x, v1._y, color);
    }
    //直线平行于y轴的情况
    else if (v1._x == v2._x)
    {
        _INT32 dir = v2._y > v1._y ? 1 : -1;
        for (auto y = v1._y; y != v2._y; y += dir)
        {
            DrawPixel(v1._x, y, color);
        }
        DrawPixel(v2._x, v2._y, color);
    }
    //直线平行于x轴的情况
    else if (v1._y == v2._y)
    {
        _INT32 dir = v2._x > v1._x ? 1 : -1;
        for (auto x = v1._x; x != v2._x; x += dir)
        {
            DrawPixel(x, v1._y, color);
        }
        DrawPixel(v2._x, v2._y, color);
    }
    //其它情况
    else
    {
        _INT32 dx = Abs(v1._x - v2._x);
        _INT32 dy = Abs(v1._y - v2._y);
        _INT32 error = 0;
        //斜率小于1的情况
        if (dx > dy)
        {
            if (v1._x > v2._x)
            {
                Swap(v1._x, v2._x);
                Swap(v1._y, v2._y);
            }
            _INT32 dir = v2._y > v1._y ? 1 : -1;
            for (auto x = v1._x, y = v1._y; x <= v2._x; x++)
            {
                DrawPixel(x, y, color);
                error += dy;
                if (error >= dx)
                {
                    error -= dx;
                    y += dir;
                    DrawPixel(x, y, color);
                }
            }
            DrawPixel(v2._x, v2._y, color);
        }
        //斜率大于1的情况
        else
        {
            if (v1._y > v2._y)
            {
                Swap(v1._x, v2._x);
                Swap(v1._y, v2._y);
            }
            _INT32 dir = v2._x > v1._x ? 1 : -1;
            for (auto y = v1._y, x = v1._x; y <= v2._y; y++)
            {
                DrawPixel(x, y, color);
                error += dx;
                if (error >= dy)
                {
                    error -= dy;
                    x += dir;
                    DrawPixel(x, y, color);
                }
            }
            DrawPixel(v2._x, v2._y, color);
        }
    }
}
复制代码
1
2
3
4
5
6
7
8
9

void inline Device::DrawPixel(_INT32 x, _INT32 y, _UINT32 color)
{
    if (x >= 0 && x < _width && y < _height && y >= 0) 
    {
        _frameBuffer[y][x] = color;
    }
}

扫描线算法

在计算扫描线的时候，三角形最好有一条边能够和x平行，但是实际情况往往并没有这么理想

对于非理想情况，如果能将其转换为上面的理想情况，处理起来就会方便许多

首先对三角形的三个顶点按照y坐标从小到大进行排序，然后分情况讨论

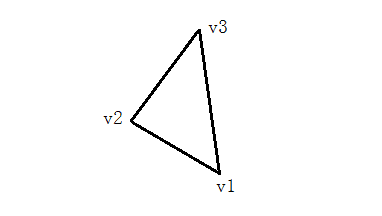
当v1v2或者v2v3在同一条直线上的时，对应之前的理想情况

除了上述两种情况外，还剩下下面两种情况，我们只需要过v2做一条平行线就能将一个三角形切割为两个理想状态下的三角形了

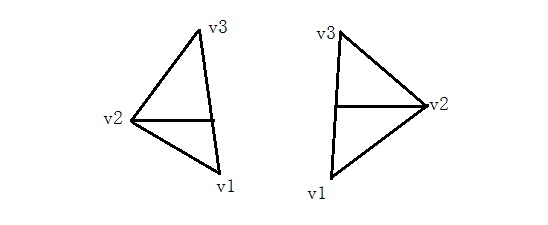
扫描线的方向最好是统一的，不然在用代码实现的时候一下子从左到右，一下子从右到左，在计算插值的时候会比较麻烦

所以对于图中的两种情况，需要去区分v1v2和v2v3到底是在v1v3的左侧还是右侧

判断的方法先过v3做一条平行于x轴的直线A，然后过v1做一条垂直于直线A的直线B，延长v1v2交直线A与点P。接下来过v1做一条平行于x轴的直线C，之后过v2做一条垂直于直线C的直线D

当v1v2和v2v3在v1v3的右侧时，辅助线如下图所示（两种情况），

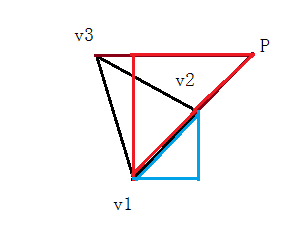
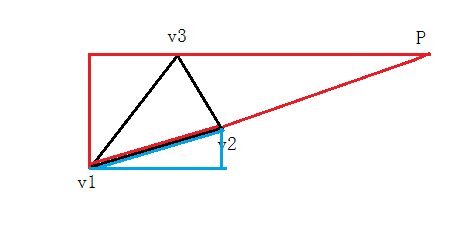
当v1v2和v2v3在v1v3的左侧时，情况和上述情况是镜像的，可以自行脑补将图片翻转

可以观察到蓝色的三角形和红色的三角形是相似的，所以可以求出P的x坐标

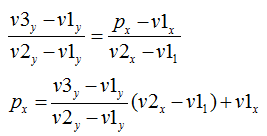
通过当p点的x坐标大于v3点的x坐标的时候，v1v2和v2v3在v1v3的右侧；反之，当p点的x坐标小于v3点的x坐标的时候，v1v2和v2v3在v1v3的左侧

这样就构造好了扫描线了，在实际渲染的时候对于每一个三角形，只需要渲染对应三角形的所有扫描线即可。

下面进行编码

Color类存储了像素的RGB信息

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Color
{

public:

    _FLOAT _r, _g, _b;

public:

    Color();

    Color(_FLOAT r, _FLOAT g, _FLOAT b);

    Color(const Color& other);

    Color& operator = (const Color& other);

public:

    Color operator + (const Color& c) const;

    Color operator + (_FLOAT offset) const;

    Color operator - (const Color& c) const;

    Color operator - (_FLOAT offset) const;

    Color operator * (const Color& c) const;

    Color operator * (_FLOAT offset) const;

};

Vertex类记录了顶点的位置，纹理坐标，颜色和深度信息，Init函数负责在对纹理坐标进行1/z插值时对顶点数据进行处理

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Vertex
{
    
public:

    Vector4f _position;
    _FLOAT _u, _v;
    Color _color;
    _FLOAT _deepz;

public:

    Vertex();

    Vertex(Vector4f position, _FLOAT u, _FLOAT v, Color color);

    Vertex(const Vertex& other);

    Vertex& operator = (const Vertex& other);

public:

    Vertex operator - (const Vertex& other) const;

    Vertex operator + (const Vertex& other) const;

    Vertex operator * (_FLOAT scale) const;

public:

    void Init();

};

Line类记录了线段的两个端点和线段上的某一个点（表示生成扫描线的时的起点或者终点）

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Line
{

public:

    Vertex _v, _vertex1, _vertex2;

public:

    Line(){}

    Line(Vertex v, Vertex vertex1, Vertex vertex2);

};

Triangle类记录了三角形的三个顶点

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Triangle
{

public:

    Vertex _vertex1, _vertex2, _vertex3;

public:

    Triangle(){}

    Triangle(Vertex vertex1, Vertex vertex2, Vertex vertex3);

public:

    bool IsTriangle() const;

};

Trapezoid记录了扫描线的集合的梯形，它记录了开始扫描的y坐标（top）和结束扫描的y坐标（bottom），以及扫描线集合梯形的两边，GetTrapezoids函数负责将不规则的三角形划分为两个上面提到的理想情况下的三角形，GetEndPoint函数负责获取扫描线的起点和终点，InitScanline函数负责获取扫描线对象

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Trapezoid
{

public:

    _FLOAT _top, _bottom;
    Line _left, _right;

public:

    Trapezoid(){}

    Trapezoid(_FLOAT top, _FLOAT bottom, Line left, Line right);

    static _INT32 GetTrapezoids(const Triangle& triangle, Trapezoid* trapezoids);

    void GetEndPoint(_FLOAT y);

    Scanline InitScanline(_INT32 y);

};
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
_INT32 Trapezoid::GetTrapezoids(const Triangle& triangle, Trapezoid* trapezoids)
{
    if (trapezoids == NULL)
    {
        return 0;
    }

    Vertex v1 = triangle._vertex1;
    Vertex v2 = triangle._vertex2;
    Vertex v3 = triangle._vertex3;
    
    //对三个点进行排序
    if (v1._position._y > v2._position._y)
    {
        Swap(v1, v2);
    }

    if (v1._position._y > v3._position._y)
    {
        Swap(v1, v3);
    }

    if (v2._position._y > v3._position._y)
    {
        Swap(v2, v3);
    }

    if (triangle.IsTriangle() == false)
    {
        return 0;
    }

    //理想情况一，v1v2平行于x轴
    if (v1._position._y == v2._position._y)
    {
        if (v1._position._x > v2._position._x)
        {
            Swap(v1, v2);
        }
        if (v1._position._y >= v3._position._y)
        {
            return 0;
        }
        trapezoids[0]._top = v1._position._y;
        trapezoids[0]._bottom = v3._position._y;
        trapezoids[0]._left._vertex1 = v1;
        trapezoids[0]._left._vertex2 = v3;
        trapezoids[0]._right._vertex1 = v2;
        trapezoids[0]._right._vertex2 = v3;
        return 1;
    }

    //理想情况二，v2v3平行于x轴
    if (v2._position._y == v3._position._y)
    {
        if (v2._position._x > v3._position._x)
        {
            Swap(v2, v3);
        }
        if (v1._position._y >= v3._position._y)
        {
            return 0;
        }
        trapezoids[0]._top = v1._position._y;
        trapezoids[0]._bottom = v3._position._y;
        trapezoids[0]._left._vertex1 = v1;
        trapezoids[0]._left._vertex2 = v2;
        trapezoids[0]._right._vertex1 = v1;
        trapezoids[0]._right._vertex2 = v3;
        return 1;
    }

    //不理想情况，需要划分三角形
    trapezoids[0]._top = v1._position._y;
    trapezoids[0]._bottom = v2._position._y;
    trapezoids[1]._top = v2._position._y;
    trapezoids[1]._bottom = v3._position._y;

    //计算P点的x坐标
    _FLOAT x, k;
    k = (v3._position._y - v1._position._y) / (v2._position._y - v1._position._y);
    x = (v2._position._x - v1._position._x) * k + v1._position._x;

    //v2在v1v3左侧时
    if (x < v3._position._x)
    {
        trapezoids[0]._left._vertex1 = v1;
        trapezoids[0]._left._vertex2 = v2;
        trapezoids[0]._right._vertex1 = v1;
        trapezoids[0]._right._vertex2 = v3;
        trapezoids[1]._left._vertex1 = v2;
        trapezoids[1]._left._vertex2 = v3;
        trapezoids[1]._right._vertex1 = v1;
        trapezoids[1]._right._vertex2 = v3;
    }
    //v2在v1v3右侧时
    else
    {
        trapezoids[0]._left._vertex1 = v1;
        trapezoids[0]._left._vertex2 = v3;
        trapezoids[0]._right._vertex1 = v1;
        trapezoids[0]._right._vertex2 = v2;
        trapezoids[1]._left._vertex1 = v1;
        trapezoids[1]._left._vertex2 = v3;
        trapezoids[1]._right._vertex1 = v2;
        trapezoids[1]._right._vertex2 = v3;
    }
    return 2;
}

Z-Buffer消隐算法

在渲染扫描线的时候，还需要考虑到深度的问题，即靠近摄像机的像素会遮挡住它后面的像素，深度检测使用的算法就是Z-Buffer消隐算法。

在前面的顶点转换并剔除视锥体外面的点后，z分量就失去了意义了，在裁剪变换的时候w分量被赋予了世界坐标系下z分量的信息，在光栅化插值的时候我们需要根据这个z分量的倒数1/z来进行插值，求出中间其它点的z分量。

z分量代表了空间中点的深度信息，即z值越小，点距离摄像机越近。为了提高性能，我们可以先计算好1/z的值，在插值和深度检测的时候统一使用1/z来进行，即1/z越大，点距离摄像机越近。

Z-Buffer消隐算法的流程如下：

  1. 屏幕上每一个位置分别有一个深度缓存（zbuffer）和像素缓存（pixelbuffer），用于记录当前位置的像素和深度信息
  2. 绘制点之前需要首先比对该点的深度值和屏幕对应位置的深度缓存中的深度值，如果比对的结果是该点距离摄像机更近，那么则更新深度缓存（zbuffer）的值并覆盖该位置的像素缓存（pixelbuffer），如果比对的结果是该点距离摄像机更远，则舍弃这个点

纹理插值

在进行纹理坐标uv插值的时候需要对u/z，v/z进行线性插值计算出新的uv值，在前面介绍坐标变换的时候已经证明过这个问题。

下面代码负责的就是渲染一个三角形

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
void Device::RenderTriangle(Vertex& v1, Vertex& v2, Vertex& v3)
{
    //对三角形的顶点进行坐标变换，将其变换到裁剪空间
    Vector4f c1 = _transform->ApplyTransform(v1._position);
    Vector4f c2 = _transform->ApplyTransform(v2._position);
    Vector4f c3 = _transform->ApplyTransform(v3._position);

    //剔除掉不在变换后的视锥长方体中的顶点
    if (_transform->CheckCVV(c1) != 0 ||
        _transform->CheckCVV(c2) != 0 ||
        _transform->CheckCVV(c3) != 0)
    {
        return;
    }

    //对变换后的顶点进行其次除法，并映射到屏幕坐标
    Vector4f h1 = _transform->Homogenize(c1);
    Vector4f h2 = _transform->Homogenize(c2);
    Vector4f h3 = _transform->Homogenize(c3);

      //非线框模式需要绘制整个三角形
    if (_renderState & (RENDER_STATE_COLOR | RENDER_STATE_TEXTURE))
    {
        Trapezoid trapezoids[2];

        //构造一个Triangle对象，坐标为屏幕坐标，w分量存储着顶点在空间中的深度信息z
        Triangle triangles = Triangle(v1, v2, v3);
        triangles._vertex1._position = h1;
        triangles._vertex2._position = h2;
        triangles._vertex3._position = h3;
        triangles._vertex1._position._w = c1._w;
        triangles._vertex2._position._w = c2._w;
        triangles._vertex3._position._w = c3._w;

        //要uv坐标进行插值1/z插值，需要先把uv变成u/z和v/z
        triangles._vertex1.Init();
        triangles._vertex2.Init();
        triangles._vertex3.Init();

        //划分三角形
        _INT32 n = Trapezoid::GetTrapezoids(triangles, trapezoids);

        if (n >= 1)
        {
            //RenderTrapezoid函数调用后面的DrawScanline函数一行一行地绘制扫描线
            RenderTrapezoid(trapezoids[0]);
        }

        if (n >= 2)
        {
            //RenderTrapezoid函数调用后面的DrawScanline函数一行一行地绘制扫描线
            RenderTrapezoid(trapezoids[1]);
        }
    }

    //线框模式只需使用Bresenham算法画线就好
    if (_renderState & RENDER_STATE_WIREFRAME)
    {
        DrawLine(Vector2i(h1), Vector2i(h2), _foreground);
        DrawLine(Vector2i(h1), Vector2i(h3), _foreground);
        DrawLine(Vector2i(h2), Vector2i(h3), _foreground);
    }
}

首先是扫描线类，定义了扫描的起始点和步长，同时记录了扫描线的起始点的x和y坐标以及扫描线的宽度，由于扫描线对应屏幕上的光栅，所以要注意扫描线的相关数据都是整形的

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Scanline
{

public:

    Vertex _start, _step;
    _INT32 _x, _y, _width;

public:

    Scanline(){}

    Scanline(Vertex start, Vertex step, _INT32 x, _INT32 y, _INT32 width);

};

下面的代码是光栅器中绘制扫描线的部分，绘制的每一个像素点之前会检查深度缓存以决定是否放弃绘制某个点，同时需要注意对插值后的uv坐标进行还原

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void Device::DrawScanline(Scanline& scanline)
{
    _UINT32* frameBuffer = _frameBuffer[scanline._y];
    _FLOAT* zBuffer = _zBuffer[scanline._y];

    //
    for (auto i = 0, x = scanline._x; i < scanline._width && x < _width; i++, x++)
    {
        if (x >= 0 && x < _width)
        {
            _FLOAT deepz = scanline._start._deepz;
            if (deepz >= zBuffer[x])
            {
                _FLOAT w = 1.0f / deepz;
                zBuffer[x] = deepz;
                if (_renderState & RENDER_STATE_COLOR)
                {
                    Color color = scanline._start._color;
                    _INT32 R = (_INT32)(color._r * 255.0f);
                    _INT32 G = (_INT32)(color._g * 255.0f);
                    _INT32 B = (_INT32)(color._b * 255.0f);
                    R = (_INT32)Range((_FLOAT)R, 0.0f, 255.0f);
                    G = (_INT32)Range((_FLOAT)G, 0.0f, 255.0f);
                    B = (_INT32)Range((_FLOAT)B, 0.0f, 255.0f);
                    frameBuffer[x] = (R << 16) | (G << 8) | (B << 0);
                }
                if (_renderState & RENDER_STATE_TEXTURE)
                {
                    //由于我们是对u/z和v/z进行插值的，所以为了得到uv坐标这里需要乘以z
                    _FLOAT u = scanline._start._u * w; 
                    _FLOAT v = scanline._start._v * w;
                    frameBuffer[x] = ReadTexture(u, v);
                }
            }
        }
        scanline._start = scanline._start + scanline._step; 
    }
}

 

 

 

 

 

 

 

 

 

最后

以上就是搞怪荷花最近收集整理的关于一个简单光栅器的实现(五) 光栅化阶段画线算法（Bresenham算法）扫描线算法Z-Buffer消隐算法纹理插值的全部内容，更多相关一个简单光栅器的实现(五)内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(77)

相关文章

OpenGL渲染管线，着色器，光栅化等概念理解
OpenGL渲染管线，着色器，光栅化等概念理解
5.10 光栅化阶段
5.10 光栅化阶段
Shader理论《三》GPU流水线之光栅化阶段
Shader理论《三》GPU流水线之光栅化阶段
iOS 性能优化面试题（光栅化）
iOS 性能优化面试题（光栅化）
一个简单光栅器的实现(五) 光栅化阶段画线算法（Bresenham算法）扫描线算法Z-Buffer消隐算法纹理插值
一个简单光栅器的实现(五) 光栅化阶段画线算法（Bresenham算法）扫描线算法Z-Buffer消隐算法纹理插值
Chromium网页CPU光栅化原理分析
Chromium网页CPU光栅化原理分析
How chromium layertreehost called
How chromium layertreehost called
计算机图形学入门·光栅化
计算机图形学入门·光栅化

评论列表共有 0 条评论

立即
投稿
返回
顶部