树的中心，经典树形dp

89 阅读 0 评论 59 点赞

我是靠谱客的博主结实钢铁侠，这篇文章主要介绍树的中心，经典树形dp，现在分享给大家，希望可以做个参考。

题目连接

给定一棵树，树中包含 n 个结点（编号1~n）和 n−1 条无向边，每条边都有一个权值。

请你在树中找到一个点，使得该点到树中其他结点的最远距离最近。

输入格式
第一行包含整数 n。
接下来 n−1 行，每行包含三个整数 ai,bi,ci，表示点 ai 和 bi 之间存在一条权值为 ci 的边。

输出格式
输出一个整数，表示所求点到树中其他结点的最远距离。

数据范围
1≤n≤10000,1≤ai,bi≤n,1≤ci≤105
输入样例：
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例：
2
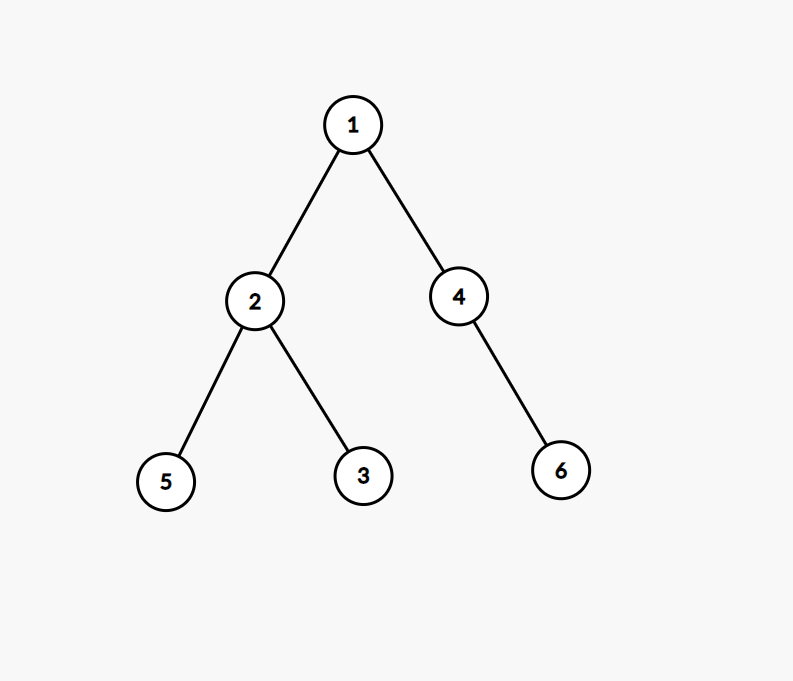
在这里插入图片描述

思路：以2号点为例：当求2号点的最大值时：
max[2] = e[2,i] + max[i].
①如果i的最大值max[i]经过2好点时，则不成立，所以此时max[i]为i号点最远距离的次大值。
②当i的最大值max[i]不经过2好点时，成立。

所以此时需要两边dfs，第一遍用子节点去更新父节点，第二遍用父节点更新子节点。

第一遍dfs:求出来所有结点不经过其父节点的最大值

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int d1[N],d2[N],p1[N];
//d1[i]表示结点i的最大距离,p1[i]表示结点i的最大距离第一个经过的子节点 
//d2[i]表示结点i的次大距离 
//第一遍dfs求出所有不经过其父节点的最大距离 
//返回x结点不经过父节点f的最大距离 
int dfs1(int x,int f){
	//x表示当前结点，f表示当前结点的父节点 
    int i;
    d1[x] = -inf;
    d2[x] = -inf;
    for(i = h[x];i!=-1;i = e[i].ne){
        int v = e[i].v,w = e[i].w;
        if(v == f)  continue;
        int t = dfs1(v,x) + w;
        if(t>d1[x]){
            p1[x] = v;
            d2[x] = d1[x];
            d1[x] = t;
        }else if(t>d2[x]){
            d2[x] = t;
        }
    }
    //如果该点的最大距离没有被更新过，则为叶子结点，距离为0 
    if(d1[x] == -inf)   d1[x] = 0;
    if(d2[x] == -inf)   d2[x] = 0;
    return d1[x];
}

问题：如何用父节点更新子节点？
在第一遍dfs时记录父节点的最远值和次远值以及最远路径最开始经过的点，对于最远路径经过的子节点，其max[子节点] = e[子节点，父节点]+父节点的次远值，与当第一遍求得的子节点的最远值取最大。

第二遍dfs：求出所有结点经过其父节点的最大值

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int up[N];
//up[i]表示经过其父节点的最大距离
//第二遍dfs求出所有点经过其父节点的最大距离 
void dfs2(int x,int f){
    int i;
    for(i = h[x];i!=-1;i=e[i].ne){
        int v = e[i].v,w = e[i].w;
        if(v == f)  continue;
        if(p1[x] != v){
        	//如果x的最大值经过子节点v,则更新up[v] 
            up[v] = max(up[x]+w,d1[x]+w);
        }else{
            up[v] = max(up[x]+w,d2[x]+w);
        }
        dfs2(v,x);
    }
    return;
}

ac代码：

复制代码

#include<iostream>
#include<cstring>

using namespace std;
const int N = 10005;
const int inf = 0x3f3f3f3f;
struct edge{
    int v,w,ne;
}e[2*N];
int h[N],idx;
void add(int a,int b,int w){
    e[idx].v = b;
    e[idx].w = w;
    e[idx].ne = h[a];
    h[a] = idx++;
}

int n;

int d1[N],d2[N],p1[N];
//d1[i]表示结点i的最大距离,p1[i]表示结点i的最大距离第一个经过的子节点 
//d2[i]表示结点i的次大距离 
//第一遍dfs求出所有不经过其父节点的最大距离 
//返回x结点不经过父节点f的最大距离 
int dfs1(int x,int f){
	//x表示当前结点，f表示当前结点的父节点 
    int i;
    d1[x] = -inf;
    d2[x] = -inf;
    for(i = h[x];i!=-1;i = e[i].ne){
        int v = e[i].v,w = e[i].w;
        if(v == f)  continue;
        int t = dfs1(v,x) + w;
        if(t>d1[x]){
            p1[x] = v;
            d2[x] = d1[x];
            d1[x] = t;
        }else if(t>d2[x]){
            d2[x] = t;
        }
    }
    //如果该点的最大距离没有被更新过，则为叶子结点，距离为0 
    if(d1[x] == -inf)   d1[x] = 0;
    if(d2[x] == -inf)   d2[x] = 0;
    return d1[x];
}

int up[N];
//up[i]表示经过其父节点的最大距离
//第二遍dfs求出所有点经过其父节点的最大距离 
void dfs2(int x,int f){
    int i;
    for(i = h[x];i!=-1;i=e[i].ne){
        int v = e[i].v,w = e[i].w;
        if(v == f)  continue;
        if(p1[x] != v){
        	//如果x的最大值经过子节点v,则更新up[v] 
            up[v] = max(up[x]+w,d1[x]+w);
        }else{
            up[v] = max(up[x]+w,d2[x]+w);
        }
        dfs2(v,x);
    }
    return;
}

int main(){
    int i,j;
    cin>>n;
    memset(h,-1,sizeof h);
    for(i =1;i<n;i++){
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
        add(b,a,c);
    }
    
    dfs1(1,-1);
    dfs2(1,-1);
    int ans = inf;
    int res;
    for(i = 1;i<=n;i++){
        res = max(d1[i],up[i]);
        ans = min(ans,res);
    }
    cout<<ans;
    
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<iostream>
#include<cstring>

using namespace std;
const int N = 10005;
const int inf = 0x3f3f3f3f;
struct edge{
    int v,w,ne;
}e[2*N];
int h[N],idx;
void add(int a,int b,int w){
    e[idx].v = b;
    e[idx].w = w;
    e[idx].ne = h[a];
    h[a] = idx++;
}

int n;


int d1[N],d2[N],p1[N];
//d1[i]表示结点i的最大距离,p1[i]表示结点i的最大距离第一个经过的子节点 
//d2[i]表示结点i的次大距离 
//第一遍dfs求出所有不经过其父节点的最大距离 
//返回x结点不经过父节点f的最大距离 
int dfs1(int x,int f){
	//x表示当前结点，f表示当前结点的父节点 
    int i;
    d1[x] = -inf;
    d2[x] = -inf;
    for(i = h[x];i!=-1;i = e[i].ne){
        int v = e[i].v,w = e[i].w;
        if(v == f)  continue;
        int t = dfs1(v,x) + w;
        if(t>d1[x]){
            p1[x] = v;
            d2[x] = d1[x];
            d1[x] = t;
        }else if(t>d2[x]){
            d2[x] = t;
        }
    }
    //如果该点的最大距离没有被更新过，则为叶子结点，距离为0 
    if(d1[x] == -inf)   d1[x] = 0;
    if(d2[x] == -inf)   d2[x] = 0;
    return d1[x];
}


int up[N];
//up[i]表示经过其父节点的最大距离
//第二遍dfs求出所有点经过其父节点的最大距离 
void dfs2(int x,int f){
    int i;
    for(i = h[x];i!=-1;i=e[i].ne){
        int v = e[i].v,w = e[i].w;
        if(v == f)  continue;
        if(p1[x] != v){
        	//如果x的最大值经过子节点v,则更新up[v] 
            up[v] = max(up[x]+w,d1[x]+w);
        }else{
            up[v] = max(up[x]+w,d2[x]+w);
        }
        dfs2(v,x);
    }
    return;
}

int main(){
    int i,j;
    cin>>n;
    memset(h,-1,sizeof h);
    for(i =1;i<n;i++){
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
        add(b,a,c);
    }
    
    dfs1(1,-1);
    dfs2(1,-1);
    int ans = inf;
    int res;
    for(i = 1;i<=n;i++){
        res = max(d1[i],up[i]);
        ans = min(ans,res);
    }
    cout<<ans;
    
    return 0;
}