uct博弈算法

Upper Confidence Bound Apply to Tree，即ucb公式应用于蒙特卡洛搜索树

前段时间用这个算法参加了计算机博弈比赛，写的很糙，以为要爆炸，没想到效果还不错。
先简单介绍一下标题的几个名词，不了解的同学想闹明白的话自行查阅相关资料。

蒙特卡洛算法

理论基础是大数定律，多次数重复模拟的各种结果的概率接近于真实概率，模拟次数越多越接近。就像那个用多个随机点求圆的面积的方法。

ucb公式

ucb值可以理解为这条路的预期价值，价值由两个部分来组成。
该节点的ucb值 = 对该节点模拟得来的平均收益 + 该节点渴望被模拟的欲望
很明显，节点被拜访的相对次数越少，欲望就越强，为的就是不放过有潜在价值的节点。
（凭什么对别人那么好，拜访那么多次？就因为第一次拜访我就让你失望了吗？就这？就再也不相信我了？）

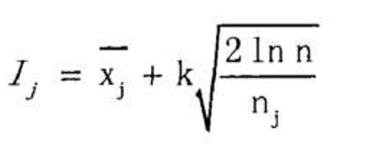
x_j就是平局收益，(k是常数，一般就是1)，n_j是当前节点被访问次数，n是当前节点的父节点的访问次数。为什么要写成这样俺也不知道，但已经被证明了这样效果最佳。

uct算法

uct算法主要有四个步骤：选择、模拟、扩展、更新

先举个不用树结构的uct算法吧（呃，这样应该就不叫uct了，应该叫ucb算法？）。总之就是只用一层孩子节点，先理解一下原理。

干说说不出个一二三来，网上清一色拿多臂赌博机举的例子，我拿井字棋举个例子吧（默认大家都知道规则），好比我们是’X’，局面如下图，该我们走子了。
_ X O
X _ O
_ O _
首先我们把当前局面状态拿出来作为根节点，现在我们有四条路可以走，那就从根节点衍生出四个子节点，每个节点对应一条走法。

刚开始并不知道这几条路哪个好，那就先认为全部走法的价值都很高（给所有孩子都赋一个无限大的ucb值），选择孩子中ucb值最大的一个（刚开始都是无限大，但后边会变），对其进行模拟（由电脑随机走子至终局），同时本身拜访次数也加一，它的父节点，这里也是根节点的拜访次数也加一，这里代表总拜访次数，用来求节点被模拟的欲望。模拟是随机模拟，可以模拟多局，得到一个平均收益。然后重新计算该节点的ucb值（肯定比无限大小了）。

我们每次都从根节点开始选ucb值最大的孩子，对它进行模拟，更新拜访次数，并得到一个新的ucb值。电脑的运行速度是很快的，虽然是随机模拟，但大数定律是跑不了的，最终我们选择ucb值最大的那条路。

现在加上树结构说一下uct算法。

大家可能有个疑问，对于上边的井字棋，其实可以直接用树结构直接把所有情况全写出来，这样不是更简单明了？为什么不这样呢？因为一般的博弈问题，像五子棋、围棋等，用树把所有情况写到底是不现实的，单一个围棋都算到世界末日了（可以搜一下）。因此一个比较好的办法就是，挑价值比较高的走法，对它进行更深层次的搜索。

深层次树结构有什么好处？
对一般博弈问题来说，如果只生成一层孩子，也许离终局还有很远，还要走n多步，而且我们的时间有限，随机模拟次数也有限，这种局面下大数定律就有点招呼不住了。uct的思想就是挖掘深层的路线，对其中表现好的（ucb值高的）进行投资（花时间对其进行模拟），而不是把时间和资源浪费在低层次的无脑模拟上。

选择、扩展、模拟、反向传播

选择：从根节点开始，计算所有孩子的ucb值，并选择其中ucb值最大的，直到到达叶子节点。

模拟：以此局面为基础随机走子模拟至终局。

扩展：若上一步选择得到的叶子节点已经被模拟过了，则往下扩展，即生孩子，反之对其进行模拟。

更新：更新模拟收益和拜访次数，不仅自己，所有祖宗都要更新，为了正确计算各个节点的ucb值。完事儿之后再从第一步选择开始，直到时间或预设次数结束。

最后我们就走第一层孩子中ucb值最大的那条路。

个人粗浅理解，可能有纰漏，欢迎补充-v-

最后

以上就是俏皮哈密瓜为你收集整理的uct博弈算法的全部内容，希望文章能够帮你解决uct博弈算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。